Empirical Likelihood with Generative AI

Moment conditions are widely used to identify parameters in models where the full likelihood is either unknown or intentionally left unspecified. Empirical likelihood methods address this problem by assigning probability weights to the observed data so that the sample moment conditions hold exactly. Building on this idea, we propose a nonparametric Bayesian framework based on exponentially tilted empirical likelihood. This Bayesian formulation is particularly appealing in settings where prior information is more naturally specified on the observables rather than on the underlying parameters. Such settings arise in the presence of auxiliary data sources or synthetic data generated by modern generative AI models.Inference proceeds by projecting posterior draws from a Dirichlet process onto the moment-restricted model, yielding a computationally efficient procedure that is naturally amenable to parallelization. We establish new Bernstein--von Mises and consistency theorems for the resulting projection posterior under both vanishing-prior and persistent-prior regimes. In an application to return prediction using overnight news headlines, we show that AI-generated auxiliary data can provide a useful source of indirect regularization when informative priors on the parameter itself are unavailable.

Generative Bayesian Filtering and Parameter Learning

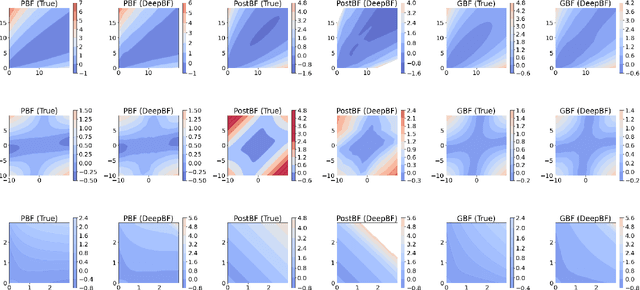
Generative Bayesian Filtering (GBF) provides a powerful and flexible framework for performing posterior inference in complex nonlinear and non-Gaussian state-space models. Our approach extends Generative Bayesian Computation (GBC) to dynamic settings, enabling recursive posterior inference using simulation-based methods powered by deep neural networks. GBF does not require explicit density evaluations, making it particularly effective when observation or transition distributions are analytically intractable. To address parameter learning, we introduce the Generative-Gibbs sampler, which bypasses explicit density evaluation by iteratively sampling each variable from its implicit full conditional distribution. Such technique is broadly applicable and enables inference in hierarchical Bayesian models with intractable densities, including state-space models. We assess the performance of the proposed methodologies through both simulated and empirical studies, including the estimation of $\alpha$-stable stochastic volatility models. Our findings indicate that GBF significantly outperforms existing likelihood-free approaches in accuracy and robustness when dealing with intractable state-space models.

Tree Bandits for Generative Bayes

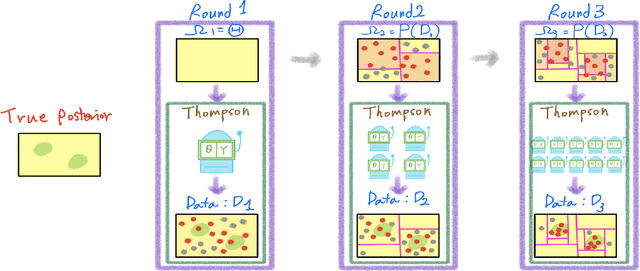
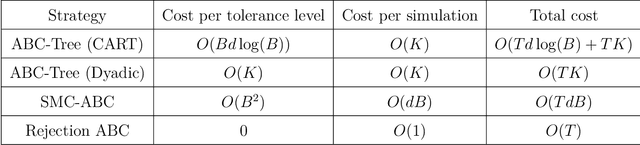
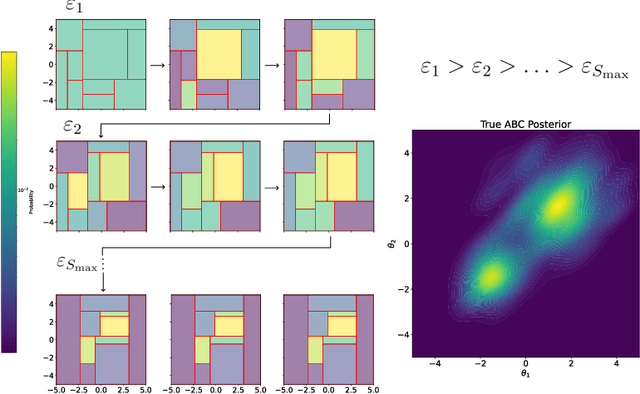
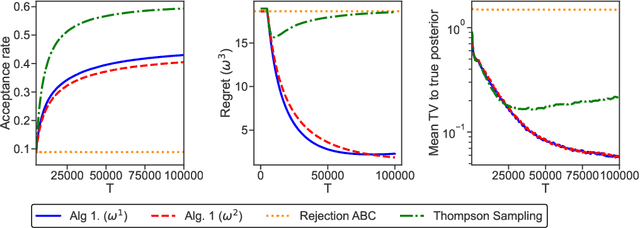
In generative models with obscured likelihood, Approximate Bayesian Computation (ABC) is often the tool of last resort for inference. However, ABC demands many prior parameter trials to keep only a small fraction that passes an acceptance test. To accelerate ABC rejection sampling, this paper develops a self-aware framework that learns from past trials and errors. We apply recursive partitioning classifiers on the ABC lookup table to sequentially refine high-likelihood regions into boxes. Each box is regarded as an arm in a binary bandit problem treating ABC acceptance as a reward. Each arm has a proclivity for being chosen for the next ABC evaluation, depending on the prior distribution and past rejections. The method places more splits in those areas where the likelihood resides, shying away from low-probability regions destined for ABC rejections. We provide two versions: (1) ABC-Tree for posterior sampling, and (2) ABC-MAP for maximum a posteriori estimation. We demonstrate accurate ABC approximability at much lower simulation cost. We justify the use of our tree-based bandit algorithms with nearly optimal regret bounds. Finally, we successfully apply our approach to the problem of masked image classification using deep generative models.

Deep Bayes Factors

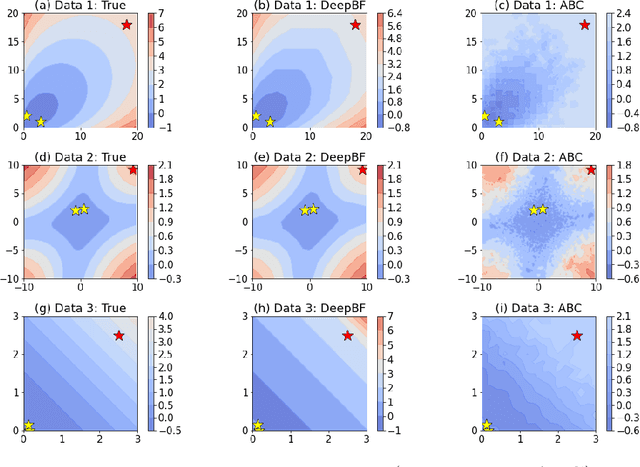
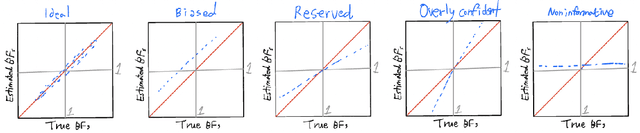
The is no other model or hypothesis verification tool in Bayesian statistics that is as widely used as the Bayes factor. We focus on generative models that are likelihood-free and, therefore, render the computation of Bayes factors (marginal likelihood ratios) far from obvious. We propose a deep learning estimator of the Bayes factor based on simulated data from two competing models using the likelihood ratio trick. This estimator is devoid of summary statistics and obviates some of the difficulties with ABC model choice. We establish sufficient conditions for consistency of our Deep Bayes Factor estimator as well as its consistency as a model selection tool. We investigate the performance of our estimator on various examples using a wide range of quality metrics related to estimation and model decision accuracy. After training, our deep learning approach enables rapid evaluations of the Bayes factor estimator at any fictional data arriving from either hypothesized model, not just the observed data $Y_0$. This allows us to inspect entire Bayes factor distributions under the two models and to quantify the relative location of the Bayes factor evaluated at $Y_0$ in light of these distributions. Such tail area evaluations are not possible for Bayes factor estimators tailored to $Y_0$. We find the performance of our Deep Bayes Factors competitive with existing MCMC techniques that require the knowledge of the likelihood function. We also consider variants for posterior or intrinsic Bayes factors estimation. We demonstrate the usefulness of our approach on a relatively high-dimensional real data example about determining cognitive biases.

Sparse Bayesian Multidimensional Item Response Theory

Multivariate Item Response Theory (MIRT) is sought-after widely by applied researchers looking for interpretable (sparse) explanations underlying response patterns in questionnaire data. There is, however, an unmet demand for such sparsity discovery tools in practice. Our paper develops a Bayesian platform for binary and ordinal item MIRT which requires minimal tuning and scales well on relatively large datasets due to its parallelizable features. Bayesian methodology for MIRT models has traditionally relied on MCMC simulation, which cannot only be slow in practice, but also often renders exact sparsity recovery impossible without additional thresholding. In this work, we develop a scalable Bayesian EM algorithm to estimate sparse factor loadings from binary and ordinal item responses. We address the seemingly insurmountable problem of unknown latent factor dimensionality with tools from Bayesian nonparametrics which enable estimating the number of factors. Rotations to sparsity through parameter expansion further enhance convergence and interpretability without identifiability constraints. In our simulation study, we show that our method reliably recovers both the factor dimensionality as well as the latent structure on high-dimensional synthetic data even for small samples. We demonstrate the practical usefulness of our approach on two datasets: an educational item response dataset and a quality-of-life measurement dataset. Both demonstrations show that our tool yields interpretable estimates, facilitating interesting discoveries that might otherwise go unnoticed under a pure confirmatory factor analysis setting. We provide an easy-to-use software which is a useful new addition to the MIRT toolkit and which will hopefully serve as the go-to method for practitioners.

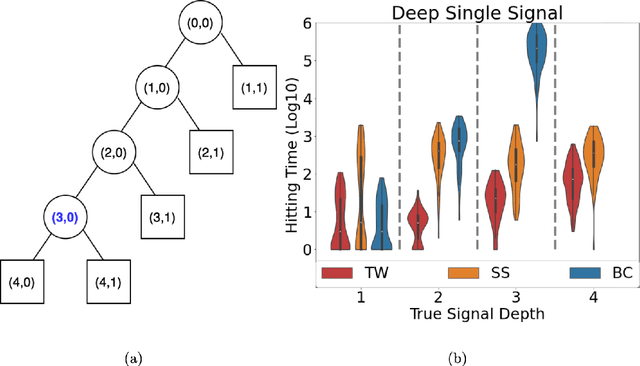
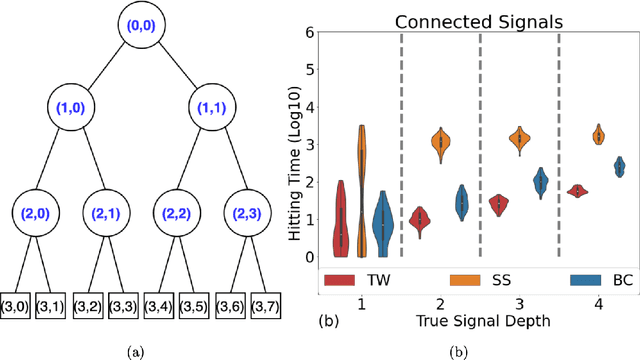
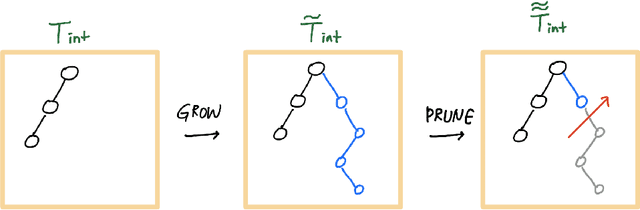
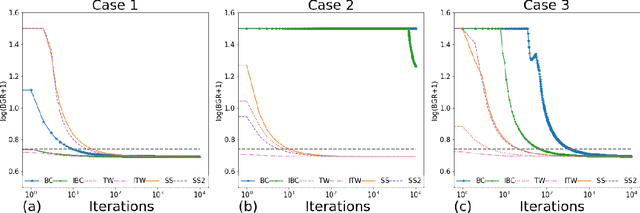
On Mixing Rates for Bayesian CART

The success of Bayesian inference with MCMC depends critically on Markov chains rapidly reaching the posterior distribution. Despite the plentitude of inferential theory for posteriors in Bayesian non-parametrics, convergence properties of MCMC algorithms that simulate from such ideal inferential targets are not thoroughly understood. This work focuses on the Bayesian CART algorithm which forms a building block of Bayesian Additive Regression Trees (BART). We derive upper bounds on mixing times for typical posteriors under various proposal distributions. Exploiting the wavelet representation of trees, we provide sufficient conditions for Bayesian CART to mix well (polynomially) under certain hierarchical connectivity restrictions on the signal. We also derive a negative result showing that Bayesian CART (based on simple grow and prune steps) cannot reach deep isolated signals in faster than exponential mixing time. To remediate myopic tree exploration, we propose Twiggy Bayesian CART which attaches/detaches entire twigs (not just single nodes) in the proposal distribution. We show polynomial mixing of Twiggy Bayesian CART without assuming that the signal is connected on a tree. Going further, we show that informed variants achieve even faster mixing. A thorough simulation study highlights discrepancies between spike-and-slab priors and Bayesian CART under a variety of proposals.

Variable Selection via Thompson Sampling

Thompson sampling is a heuristic algorithm for the multi-armed bandit problem which has a long tradition in machine learning. The algorithm has a Bayesian spirit in the sense that it selects arms based on posterior samples of reward probabilities of each arm. By forging a connection between combinatorial binary bandits and spike-and-slab variable selection, we propose a stochastic optimization approach to subset selection called Thompson Variable Selection (TVS). TVS is a framework for interpretable machine learning which does not rely on the underlying model to be linear. TVS brings together Bayesian reinforcement and machine learning in order to extend the reach of Bayesian subset selection to non-parametric models and large datasets with very many predictors and/or very many observations. Depending on the choice of a reward, TVS can be deployed in offline as well as online setups with streaming data batches. Tailoring multiplay bandits to variable selection, we provide regret bounds without necessarily assuming that the arm mean rewards be unrelated. We show a very strong empirical performance on both simulated and real data. Unlike deterministic optimization methods for spike-and-slab variable selection, the stochastic nature makes TVS less prone to local convergence and thereby more robust.

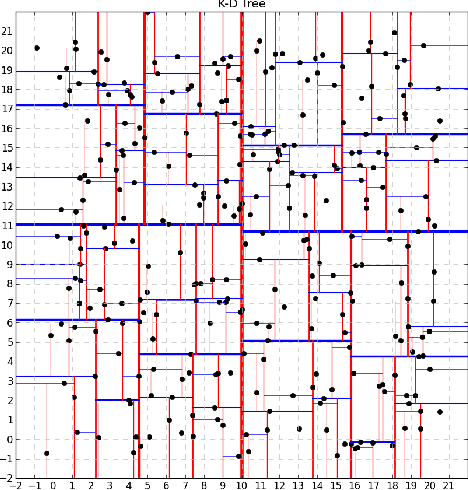
On Theory for BART

Ensemble learning is a statistical paradigm built on the premise that many weak learners can perform exceptionally well when deployed collectively. The BART method of Chipman et al. (2010) is a prominent example of Bayesian ensemble learning, where each learner is a tree. Due to its impressive performance, BART has received a lot of attention from practitioners. Despite its wide popularity, however, theoretical studies of BART have begun emerging only very recently. Laying the foundations for the theoretical analysis of Bayesian forests, Rockova and van der Pas (2017) showed optimal posterior concentration under conditionally uniform tree priors. These priors deviate from the actual priors implemented in BART. Here, we study the exact BART prior and propose a simple modification so that it also enjoys optimality properties. To this end, we dive into branching process theory. We obtain tail bounds for the distribution of total progeny under heterogeneous Galton-Watson (GW) processes exploiting their connection to random walks. We conclude with a result stating the optimal rate of posterior convergence for BART.

Posterior Concentration for Sparse Deep Learning

Spike-and-Slab Deep Learning (SS-DL) is a fully Bayesian alternative to Dropout for improving generalizability of deep ReLU networks. This new type of regularization enables provable recovery of smooth input-output maps with unknown levels of smoothness. Indeed, we show that the posterior distribution concentrates at the near minimax rate for $\alpha$-H\"older smooth maps, performing as well as if we knew the smoothness level $\alpha$ ahead of time. Our result sheds light on architecture design for deep neural networks, namely the choice of depth, width and sparsity level. These network attributes typically depend on unknown smoothness in order to be optimal. We obviate this constraint with the fully Bayes construction. As an aside, we show that SS-DL does not overfit in the sense that the posterior concentrates on smaller networks with fewer (up to the optimal number of) nodes and links. Our results provide new theoretical justifications for deep ReLU networks from a Bayesian point of view.