Deep Bayes Factors

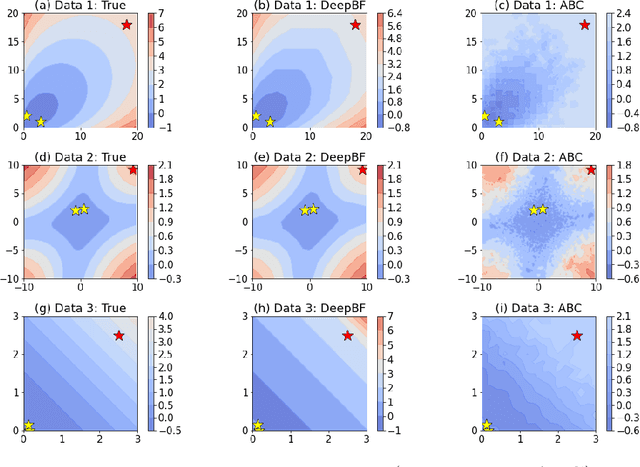
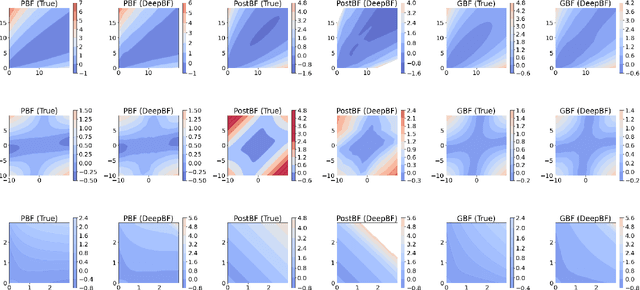
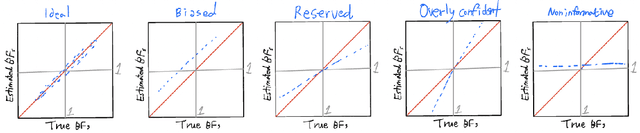
The is no other model or hypothesis verification tool in Bayesian statistics that is as widely used as the Bayes factor. We focus on generative models that are likelihood-free and, therefore, render the computation of Bayes factors (marginal likelihood ratios) far from obvious. We propose a deep learning estimator of the Bayes factor based on simulated data from two competing models using the likelihood ratio trick. This estimator is devoid of summary statistics and obviates some of the difficulties with ABC model choice. We establish sufficient conditions for consistency of our Deep Bayes Factor estimator as well as its consistency as a model selection tool. We investigate the performance of our estimator on various examples using a wide range of quality metrics related to estimation and model decision accuracy. After training, our deep learning approach enables rapid evaluations of the Bayes factor estimator at any fictional data arriving from either hypothesized model, not just the observed data $Y_0$. This allows us to inspect entire Bayes factor distributions under the two models and to quantify the relative location of the Bayes factor evaluated at $Y_0$ in light of these distributions. Such tail area evaluations are not possible for Bayes factor estimators tailored to $Y_0$. We find the performance of our Deep Bayes Factors competitive with existing MCMC techniques that require the knowledge of the likelihood function. We also consider variants for posterior or intrinsic Bayes factors estimation. We demonstrate the usefulness of our approach on a relatively high-dimensional real data example about determining cognitive biases.