Deep Generative Quantile Bayes

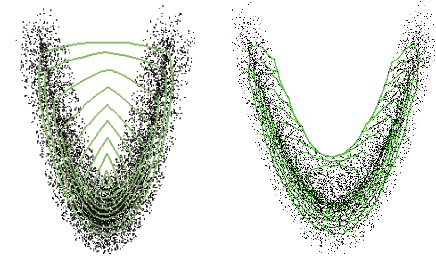
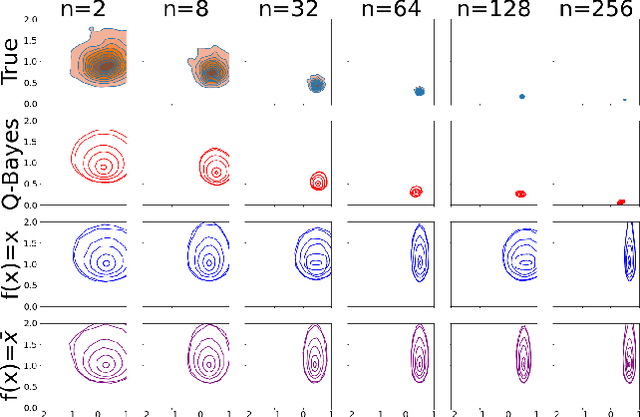
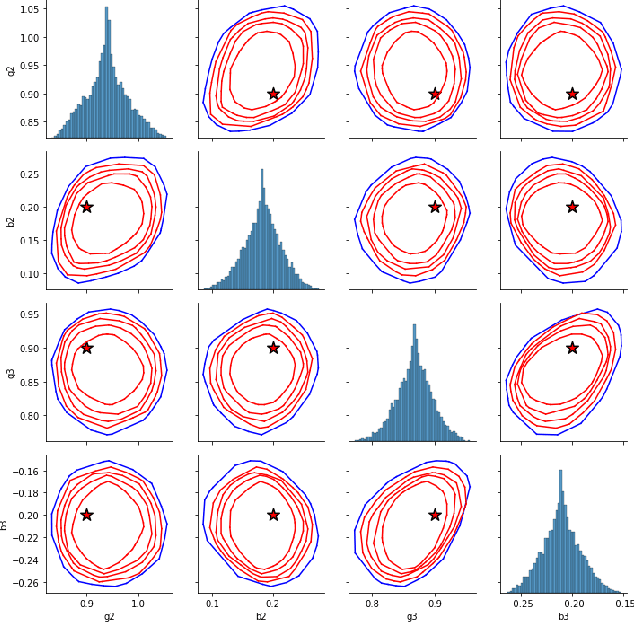
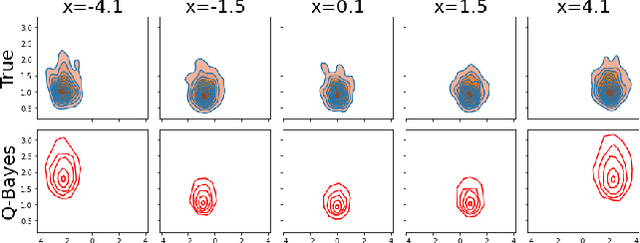
We develop a multivariate posterior sampling procedure through deep generative quantile learning. Simulation proceeds implicitly through a push-forward mapping that can transform i.i.d. random vector samples from the posterior. We utilize Monge-Kantorovich depth in multivariate quantiles to directly sample from Bayesian credible sets, a unique feature not offered by typical posterior sampling methods. To enhance the training of the quantile mapping, we design a neural network that automatically performs summary statistic extraction. This additional neural network structure has performance benefits, including support shrinkage (i.e., contraction of our posterior approximation) as the observation sample size increases. We demonstrate the usefulness of our approach on several examples where the absence of likelihood renders classical MCMC infeasible. Finally, we provide the following frequentist theoretical justifications for our quantile learning framework: {consistency of the estimated vector quantile, of the recovered posterior distribution, and of the corresponding Bayesian credible sets.

Inductive Global and Local Manifold Approximation and Projection

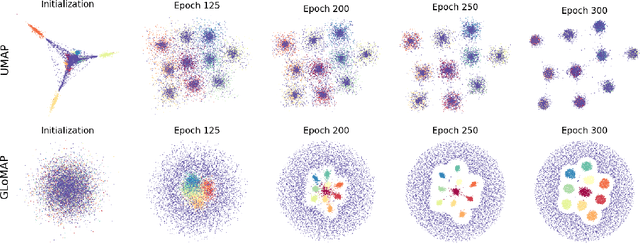
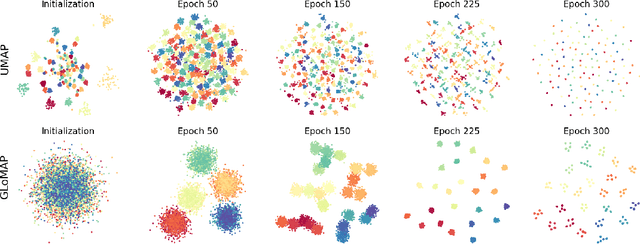
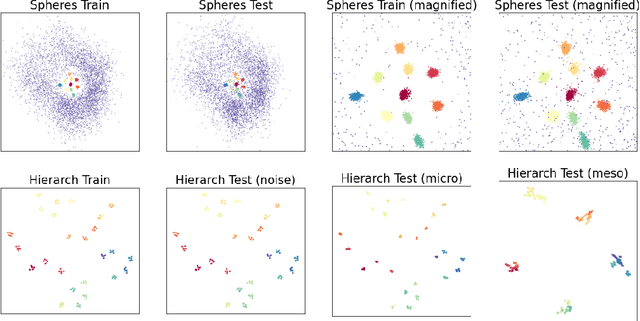
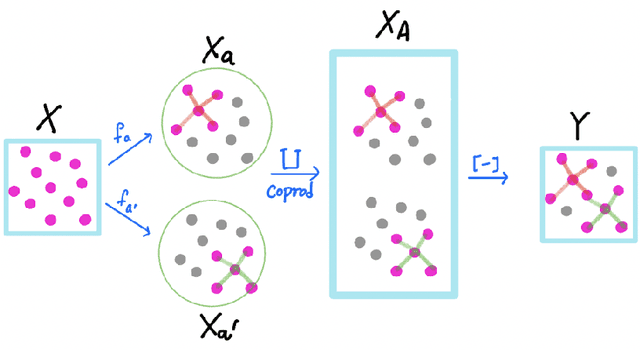
Nonlinear dimensional reduction with the manifold assumption, often called manifold learning, has proven its usefulness in a wide range of high-dimensional data analysis. The significant impact of t-SNE and UMAP has catalyzed intense research interest, seeking further innovations toward visualizing not only the local but also the global structure information of the data. Moreover, there have been consistent efforts toward generalizable dimensional reduction that handles unseen data. In this paper, we first propose GLoMAP, a novel manifold learning method for dimensional reduction and high-dimensional data visualization. GLoMAP preserves locally and globally meaningful distance estimates and displays a progression from global to local formation during the course of optimization. Furthermore, we extend GLoMAP to its inductive version, iGLoMAP, which utilizes a deep neural network to map data to its lower-dimensional representation. This allows iGLoMAP to provide lower-dimensional embeddings for unseen points without needing to re-train the algorithm. iGLoMAP is also well-suited for mini-batch learning, enabling large-scale, accelerated gradient calculations. We have successfully applied both GLoMAP and iGLoMAP to the simulated and real-data settings, with competitive experiments against the state-of-the-art methods.

Tree Bandits for Generative Bayes

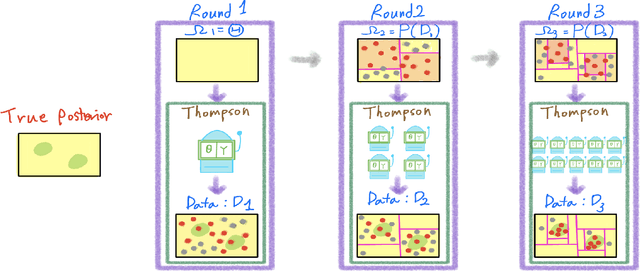
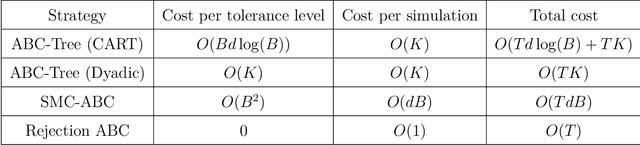
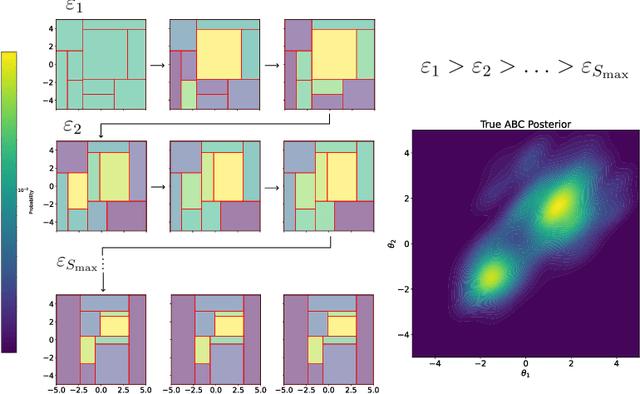
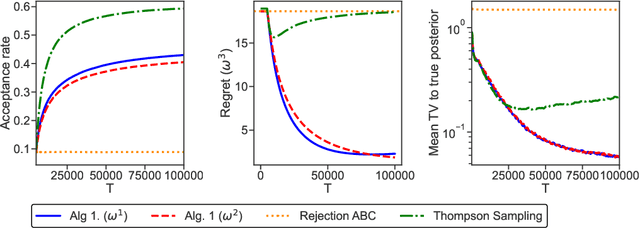
In generative models with obscured likelihood, Approximate Bayesian Computation (ABC) is often the tool of last resort for inference. However, ABC demands many prior parameter trials to keep only a small fraction that passes an acceptance test. To accelerate ABC rejection sampling, this paper develops a self-aware framework that learns from past trials and errors. We apply recursive partitioning classifiers on the ABC lookup table to sequentially refine high-likelihood regions into boxes. Each box is regarded as an arm in a binary bandit problem treating ABC acceptance as a reward. Each arm has a proclivity for being chosen for the next ABC evaluation, depending on the prior distribution and past rejections. The method places more splits in those areas where the likelihood resides, shying away from low-probability regions destined for ABC rejections. We provide two versions: (1) ABC-Tree for posterior sampling, and (2) ABC-MAP for maximum a posteriori estimation. We demonstrate accurate ABC approximability at much lower simulation cost. We justify the use of our tree-based bandit algorithms with nearly optimal regret bounds. Finally, we successfully apply our approach to the problem of masked image classification using deep generative models.

Deep Bayes Factors

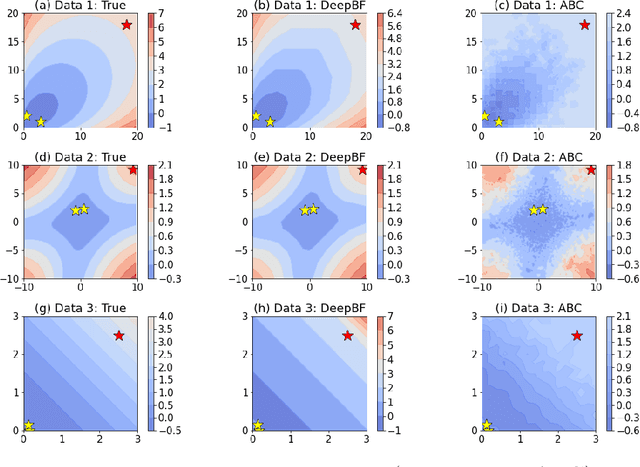
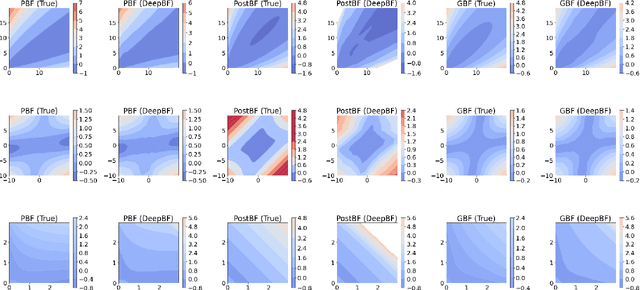
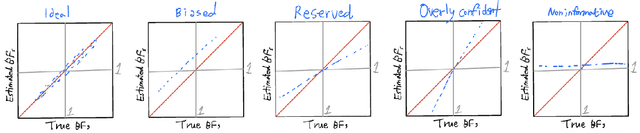
The is no other model or hypothesis verification tool in Bayesian statistics that is as widely used as the Bayes factor. We focus on generative models that are likelihood-free and, therefore, render the computation of Bayes factors (marginal likelihood ratios) far from obvious. We propose a deep learning estimator of the Bayes factor based on simulated data from two competing models using the likelihood ratio trick. This estimator is devoid of summary statistics and obviates some of the difficulties with ABC model choice. We establish sufficient conditions for consistency of our Deep Bayes Factor estimator as well as its consistency as a model selection tool. We investigate the performance of our estimator on various examples using a wide range of quality metrics related to estimation and model decision accuracy. After training, our deep learning approach enables rapid evaluations of the Bayes factor estimator at any fictional data arriving from either hypothesized model, not just the observed data $Y_0$. This allows us to inspect entire Bayes factor distributions under the two models and to quantify the relative location of the Bayes factor evaluated at $Y_0$ in light of these distributions. Such tail area evaluations are not possible for Bayes factor estimators tailored to $Y_0$. We find the performance of our Deep Bayes Factors competitive with existing MCMC techniques that require the knowledge of the likelihood function. We also consider variants for posterior or intrinsic Bayes factors estimation. We demonstrate the usefulness of our approach on a relatively high-dimensional real data example about determining cognitive biases.

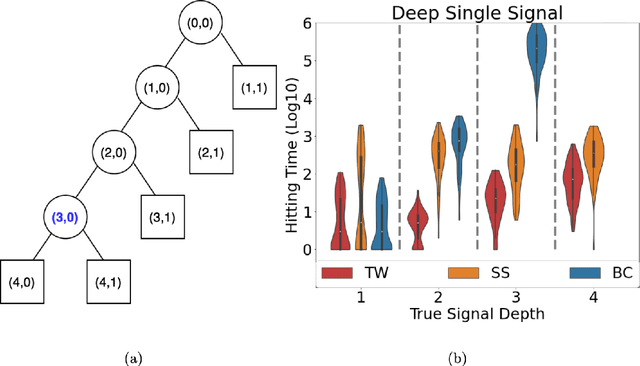
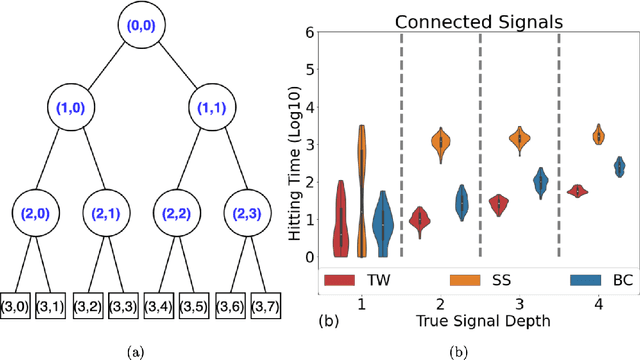
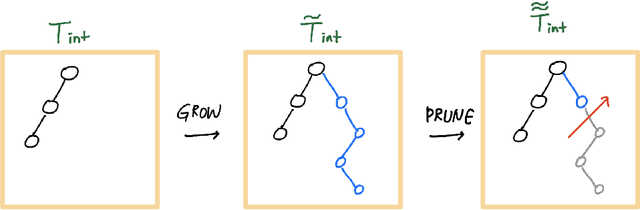
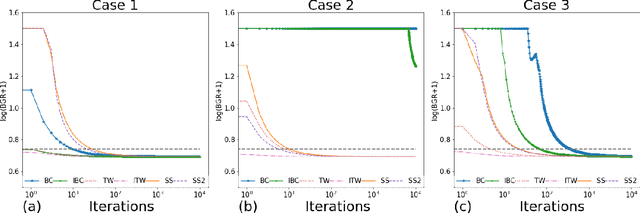
On Mixing Rates for Bayesian CART

The success of Bayesian inference with MCMC depends critically on Markov chains rapidly reaching the posterior distribution. Despite the plentitude of inferential theory for posteriors in Bayesian non-parametrics, convergence properties of MCMC algorithms that simulate from such ideal inferential targets are not thoroughly understood. This work focuses on the Bayesian CART algorithm which forms a building block of Bayesian Additive Regression Trees (BART). We derive upper bounds on mixing times for typical posteriors under various proposal distributions. Exploiting the wavelet representation of trees, we provide sufficient conditions for Bayesian CART to mix well (polynomially) under certain hierarchical connectivity restrictions on the signal. We also derive a negative result showing that Bayesian CART (based on simple grow and prune steps) cannot reach deep isolated signals in faster than exponential mixing time. To remediate myopic tree exploration, we propose Twiggy Bayesian CART which attaches/detaches entire twigs (not just single nodes) in the proposal distribution. We show polynomial mixing of Twiggy Bayesian CART without assuming that the signal is connected on a tree. Going further, we show that informed variants achieve even faster mixing. A thorough simulation study highlights discrepancies between spike-and-slab priors and Bayesian CART under a variety of proposals.

Robust Sensible Adversarial Learning of Deep Neural Networks for Image Classification

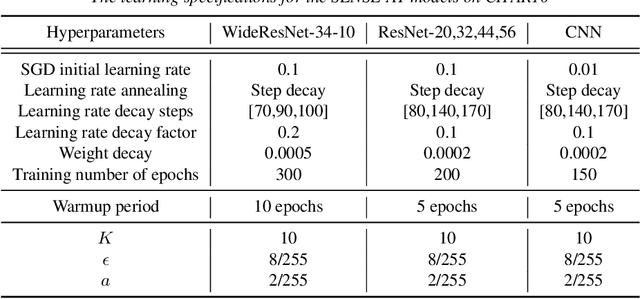
The idea of robustness is central and critical to modern statistical analysis. However, despite the recent advances of deep neural networks (DNNs), many studies have shown that DNNs are vulnerable to adversarial attacks. Making imperceptible changes to an image can cause DNN models to make the wrong classification with high confidence, such as classifying a benign mole as a malignant tumor and a stop sign as a speed limit sign. The trade-off between robustness and standard accuracy is common for DNN models. In this paper, we introduce sensible adversarial learning and demonstrate the synergistic effect between pursuits of standard natural accuracy and robustness. Specifically, we define a sensible adversary which is useful for learning a robust model while keeping high natural accuracy. We theoretically establish that the Bayes classifier is the most robust multi-class classifier with the 0-1 loss under sensible adversarial learning. We propose a novel and efficient algorithm that trains a robust model using implicit loss truncation. We apply sensible adversarial learning for large-scale image classification to a handwritten digital image dataset called MNIST and an object recognition colored image dataset called CIFAR10. We have performed an extensive comparative study to compare our method with other competitive methods. Our experiments empirically demonstrate that our method is not sensitive to its hyperparameter and does not collapse even with a small model capacity while promoting robustness against various attacks and keeping high natural accuracy.