Deep Generative Quantile Bayes

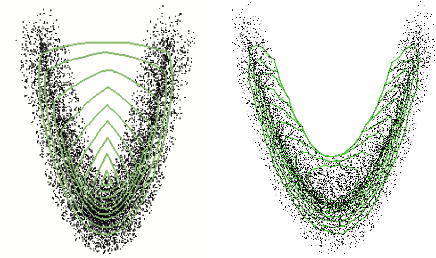
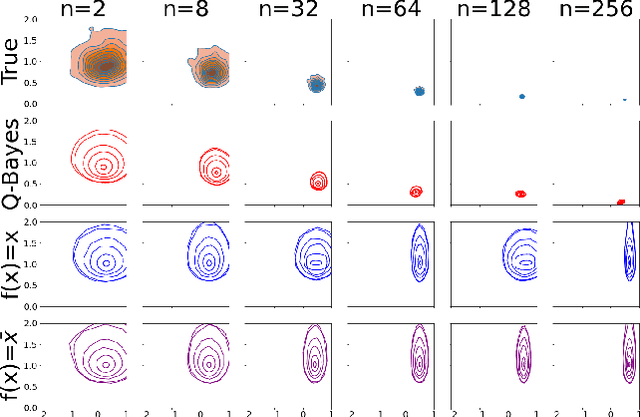
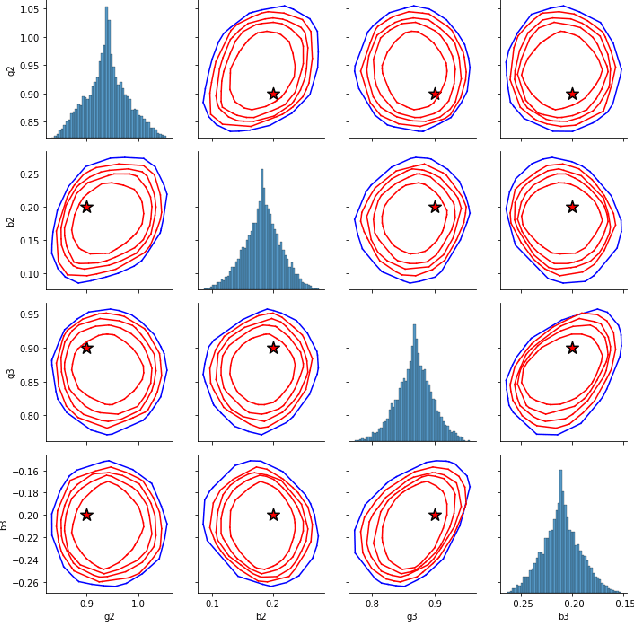
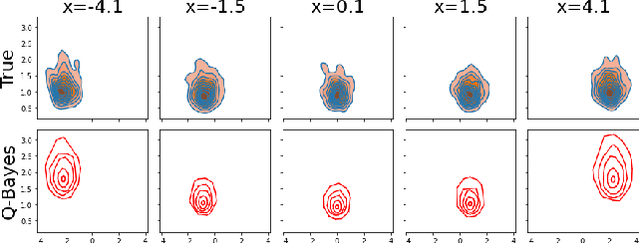
We develop a multivariate posterior sampling procedure through deep generative quantile learning. Simulation proceeds implicitly through a push-forward mapping that can transform i.i.d. random vector samples from the posterior. We utilize Monge-Kantorovich depth in multivariate quantiles to directly sample from Bayesian credible sets, a unique feature not offered by typical posterior sampling methods. To enhance the training of the quantile mapping, we design a neural network that automatically performs summary statistic extraction. This additional neural network structure has performance benefits, including support shrinkage (i.e., contraction of our posterior approximation) as the observation sample size increases. We demonstrate the usefulness of our approach on several examples where the absence of likelihood renders classical MCMC infeasible. Finally, we provide the following frequentist theoretical justifications for our quantile learning framework: {consistency of the estimated vector quantile, of the recovered posterior distribution, and of the corresponding Bayesian credible sets.

Adversarial Bayesian Simulation

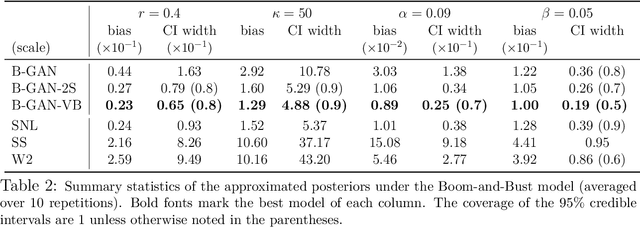
In the absence of explicit or tractable likelihoods, Bayesians often resort to approximate Bayesian computation (ABC) for inference. Our work bridges ABC with deep neural implicit samplers based on generative adversarial networks (GANs) and adversarial variational Bayes. Both ABC and GANs compare aspects of observed and fake data to simulate from posteriors and likelihoods, respectively. We develop a Bayesian GAN (B-GAN) sampler that directly targets the posterior by solving an adversarial optimization problem. B-GAN is driven by a deterministic mapping learned on the ABC reference by conditional GANs. Once the mapping has been trained, iid posterior samples are obtained by filtering noise at a negligible additional cost. We propose two post-processing local refinements using (1) data-driven proposals with importance reweighing, and (2) variational Bayes. We support our findings with frequentist-Bayesian results, showing that the typical total variation distance between the true and approximate posteriors converges to zero for certain neural network generators and discriminators. Our findings on simulated data show highly competitive performance relative to some of the most recent likelihood-free posterior simulators.

Approximate Bayesian Computation via Classification

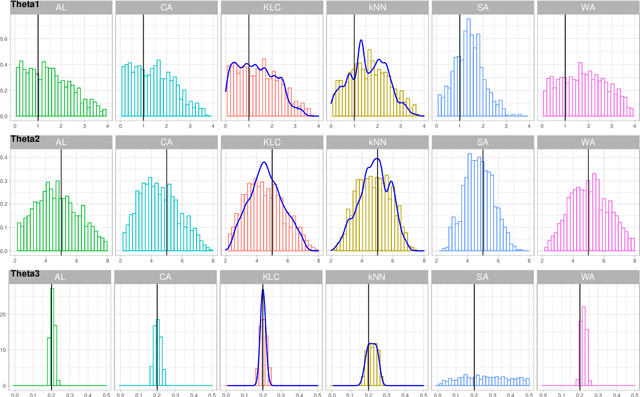
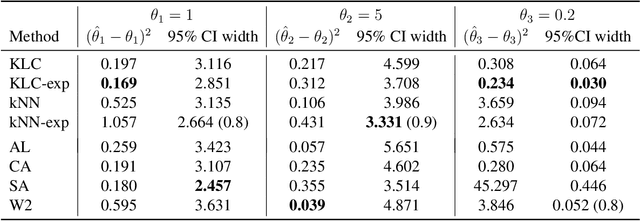
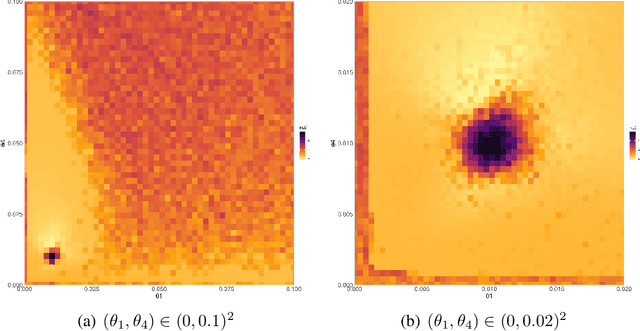
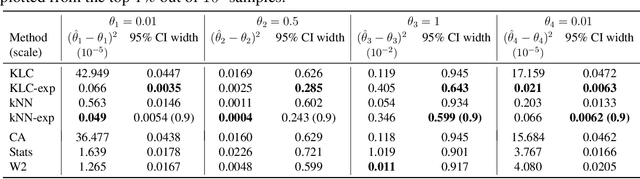
Approximate Bayesian Computation (ABC) enables statistical inference in complex models whose likelihoods are difficult to calculate but easy to simulate from. ABC constructs a kernel-type approximation to the posterior distribution through an accept/reject mechanism which compares summary statistics of real and simulated data. To obviate the need for summary statistics, we directly compare empirical distributions with a Kullback-Leibler (KL) divergence estimator obtained via classification. In particular, we blend flexible machine learning classifiers within ABC to automate fake/real data comparisons. We consider the traditional accept/reject kernel as well as an exponential weighting scheme which does not require the ABC acceptance threshold. Our theoretical results show that the rate at which our ABC posterior distributions concentrate around the true parameter depends on the estimation error of the classifier. We derive limiting posterior shape results and find that, with a properly scaled exponential kernel, asymptotic normality holds. We demonstrate the usefulness of our approach on simulated examples as well as real data in the context of stock volatility estimation.

Uncertainty Quantification for Sparse Deep Learning

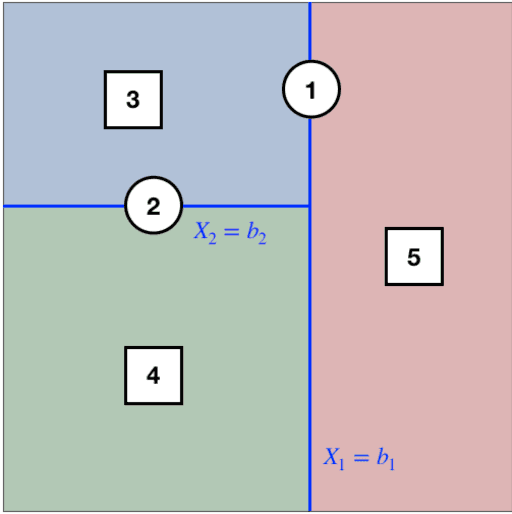
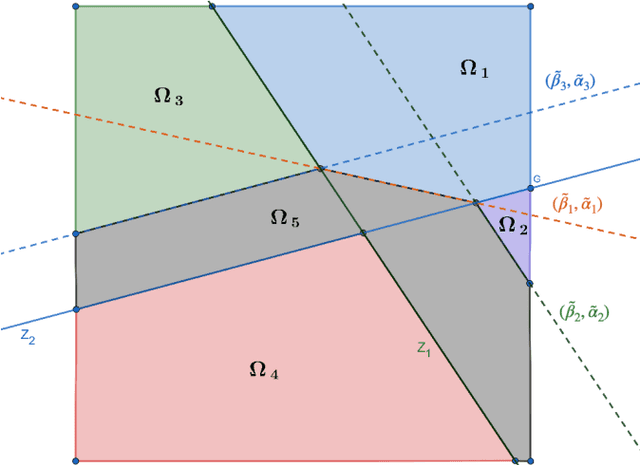
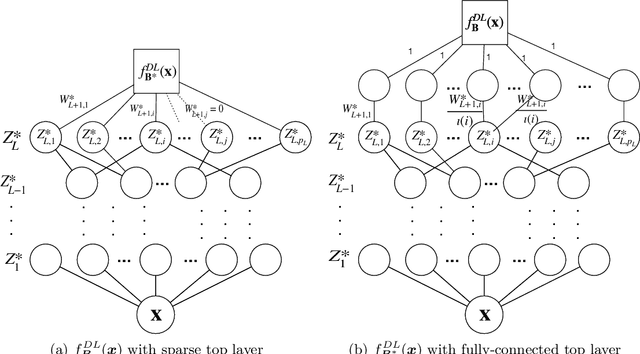
Deep learning methods continue to have a decided impact on machine learning, both in theory and in practice. Statistical theoretical developments have been mostly concerned with approximability or rates of estimation when recovering infinite dimensional objects (curves or densities). Despite the impressive array of available theoretical results, the literature has been largely silent about uncertainty quantification for deep learning. This paper takes a step forward in this important direction by taking a Bayesian point of view. We study Gaussian approximability of certain aspects of posterior distributions of sparse deep ReLU architectures in non-parametric regression. Building on tools from Bayesian non-parametrics, we provide semi-parametric Bernstein-von Mises theorems for linear and quadratic functionals, which guarantee that implied Bayesian credible regions have valid frequentist coverage. Our results provide new theoretical justifications for (Bayesian) deep learning with ReLU activation functions, highlighting their inferential potential.