Conditional Flow Matching for Bayesian Posterior Inference

We propose a generative multivariate posterior sampler via flow matching. It offers a simple training objective, and does not require access to likelihood evaluation. The method learns a dynamic, block-triangular velocity field in the joint space of data and parameters, which results in a deterministic transport map from a source distribution to the desired posterior. The inverse map, named vector rank, is accessible by reversibly integrating the velocity over time. It is advantageous to leverage the dynamic design: proper constraints on the velocity yield a monotone map, which leads to a conditional Brenier map, enabling a fast and simultaneous generation of Bayesian credible sets whose contours correspond to level sets of Monge-Kantorovich data depth. Our approach is computationally lighter compared to GAN-based and diffusion-based counterparts, and is capable of capturing complex posterior structures. Finally, frequentist theoretical guarantee on the consistency of the recovered posterior distribution, and of the corresponding Bayesian credible sets, is provided.

Deep Generative Quantile Bayes

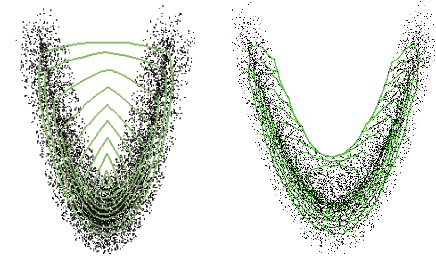
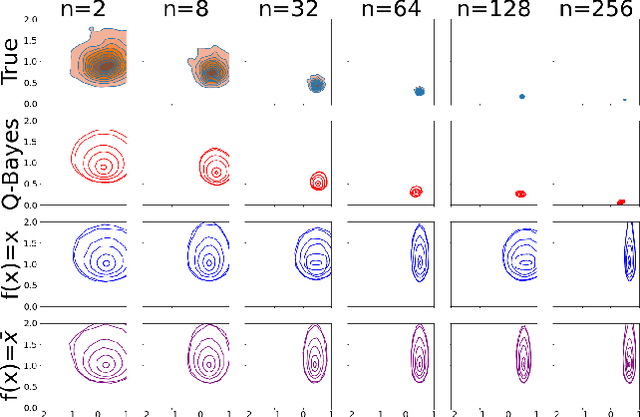
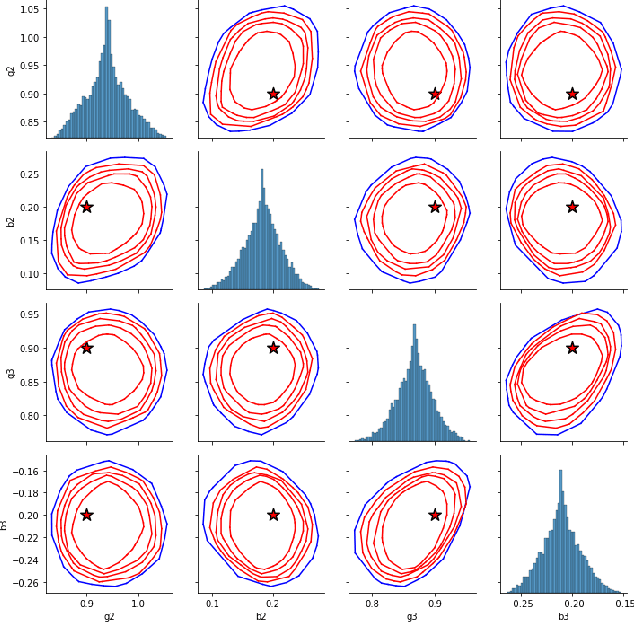
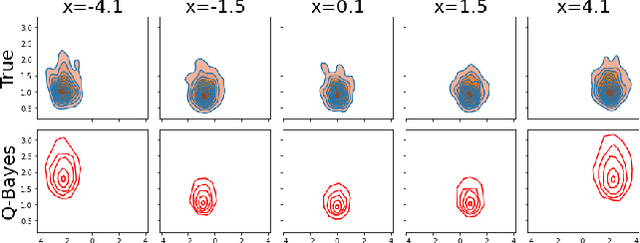
We develop a multivariate posterior sampling procedure through deep generative quantile learning. Simulation proceeds implicitly through a push-forward mapping that can transform i.i.d. random vector samples from the posterior. We utilize Monge-Kantorovich depth in multivariate quantiles to directly sample from Bayesian credible sets, a unique feature not offered by typical posterior sampling methods. To enhance the training of the quantile mapping, we design a neural network that automatically performs summary statistic extraction. This additional neural network structure has performance benefits, including support shrinkage (i.e., contraction of our posterior approximation) as the observation sample size increases. We demonstrate the usefulness of our approach on several examples where the absence of likelihood renders classical MCMC infeasible. Finally, we provide the following frequentist theoretical justifications for our quantile learning framework: {consistency of the estimated vector quantile, of the recovered posterior distribution, and of the corresponding Bayesian credible sets.