Tree Bandits for Generative Bayes
Paper and Code
Apr 16, 2024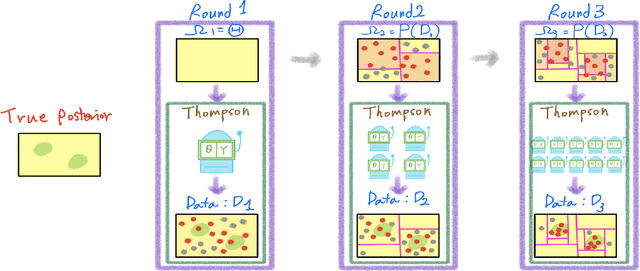
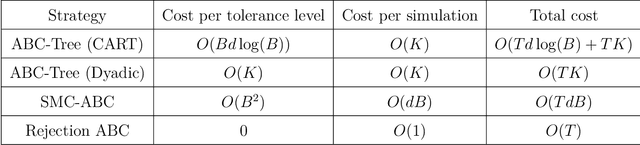
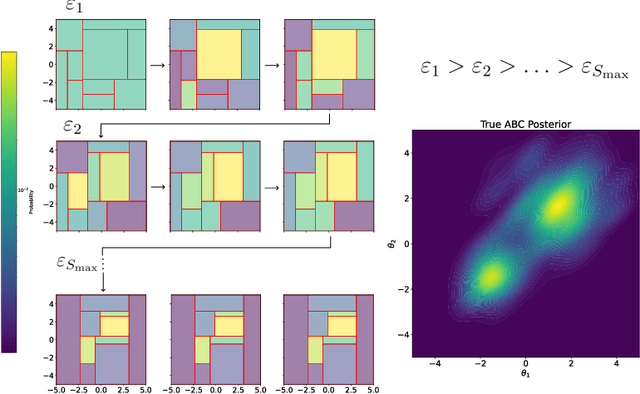
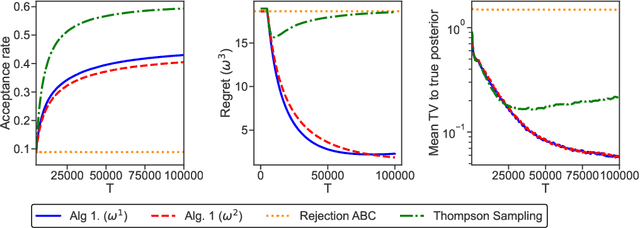
In generative models with obscured likelihood, Approximate Bayesian Computation (ABC) is often the tool of last resort for inference. However, ABC demands many prior parameter trials to keep only a small fraction that passes an acceptance test. To accelerate ABC rejection sampling, this paper develops a self-aware framework that learns from past trials and errors. We apply recursive partitioning classifiers on the ABC lookup table to sequentially refine high-likelihood regions into boxes. Each box is regarded as an arm in a binary bandit problem treating ABC acceptance as a reward. Each arm has a proclivity for being chosen for the next ABC evaluation, depending on the prior distribution and past rejections. The method places more splits in those areas where the likelihood resides, shying away from low-probability regions destined for ABC rejections. We provide two versions: (1) ABC-Tree for posterior sampling, and (2) ABC-MAP for maximum a posteriori estimation. We demonstrate accurate ABC approximability at much lower simulation cost. We justify the use of our tree-based bandit algorithms with nearly optimal regret bounds. Finally, we successfully apply our approach to the problem of masked image classification using deep generative models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge