Fast exact recovery of noisy matrix from few entries: the infinity norm approach

The matrix recovery (completion) problem, a central problem in data science and theoretical computer science, is to recover a matrix $A$ from a relatively small sample of entries. While such a task is impossible in general, it has been shown that one can recover $A$ exactly in polynomial time, with high probability, from a random subset of entries, under three (basic and necessary) assumptions: (1) the rank of $A$ is very small compared to its dimensions (low rank), (2) $A$ has delocalized singular vectors (incoherence), and (3) the sample size is sufficiently large. There are many different algorithms for the task, including convex optimization by Candes, Tao and Recht (2009), alternating projection by Hardt and Wooters (2014) and low rank approximation with gradient descent by Keshavan, Montanari and Oh (2009, 2010). In applications, it is more realistic to assume that data is noisy. In this case, these approaches provide an approximate recovery with small root mean square error. However, it is hard to transform such approximate recovery to an exact one. Recently, results by Abbe et al. (2017) and Bhardwaj et al. (2023) concerning approximation in the infinity norm showed that we can achieve exact recovery even in the noisy case, given that the ground matrix has bounded precision. Beyond the three basic assumptions above, they required either the condition number of $A$ is small (Abbe et al.) or the gap between consecutive singular values is large (Bhardwaj et al.). In this paper, we remove these extra spectral assumptions. As a result, we obtain a simple algorithm for exact recovery in the noisy case, under only three basic assumptions. This is the first such algorithm. To analyse the algorithm, we introduce a contour integration argument which is totally different from all previous methods and may be of independent interest.

VinDr-Mammo: A large-scale benchmark dataset for computer-aided diagnosis in full-field digital mammography

Mammography, or breast X-ray, is the most widely used imaging modality to detect cancer and other breast diseases. Recent studies have shown that deep learning-based computer-assisted detection and diagnosis (CADe or CADx) tools have been developed to support physicians and improve the accuracy of interpreting mammography. However, most published datasets of mammography are either limited on sample size or digitalized from screen-film mammography (SFM), hindering the development of CADe and CADx tools which are developed based on full-field digital mammography (FFDM). To overcome this challenge, we introduce VinDr-Mammo - a new benchmark dataset of FFDM for detecting and diagnosing breast cancer and other diseases in mammography. The dataset consists of 5,000 mammography exams, each of which has four standard views and is double read with disagreement (if any) being resolved by arbitration. It is created for the assessment of Breast Imaging Reporting and Data System (BI-RADS) and density at the breast level. In addition, the dataset also provides the category, location, and BI-RADS assessment of non-benign findings. We make VinDr-Mammo publicly available on PhysioNet as a new imaging resource to promote advances in developing CADe and CADx tools for breast cancer screening.

VinDr-SpineXR: A deep learning framework for spinal lesions detection and classification from radiographs

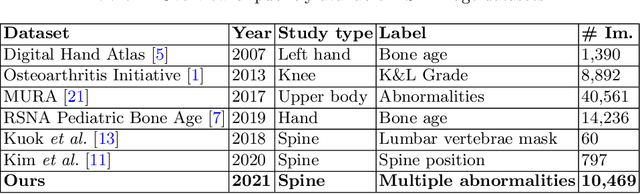
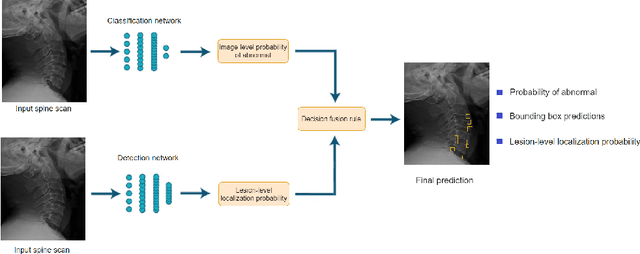
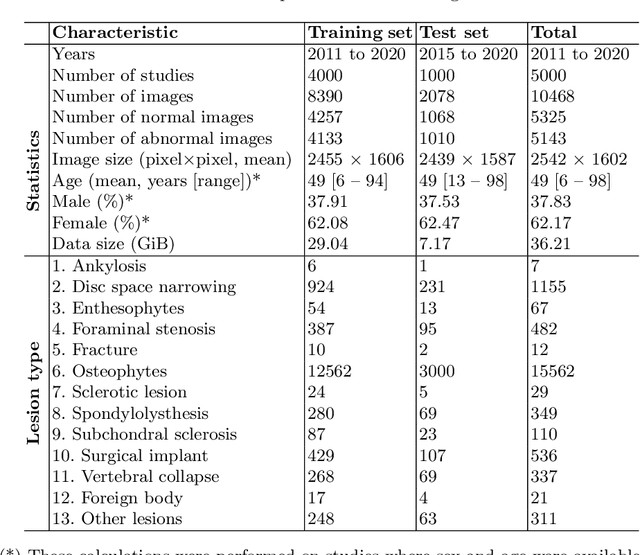
Radiographs are used as the most important imaging tool for identifying spine anomalies in clinical practice. The evaluation of spinal bone lesions, however, is a challenging task for radiologists. This work aims at developing and evaluating a deep learning-based framework, named VinDr-SpineXR, for the classification and localization of abnormalities from spine X-rays. First, we build a large dataset, comprising 10,468 spine X-ray images from 5,000 studies, each of which is manually annotated by an experienced radiologist with bounding boxes around abnormal findings in 13 categories. Using this dataset, we then train a deep learning classifier to determine whether a spine scan is abnormal and a detector to localize 7 crucial findings amongst the total 13. The VinDr-SpineXR is evaluated on a test set of 2,078 images from 1,000 studies, which is kept separate from the training set. It demonstrates an area under the receiver operating characteristic curve (AUROC) of 88.61% (95% CI 87.19%, 90.02%) for the image-level classification task and a mean average precision (mAP@0.5) of 33.56% for the lesion-level localization task. These results serve as a proof of concept and set a baseline for future research in this direction. To encourage advances, the dataset, codes, and trained deep learning models are made publicly available.

VinDr-CXR: An open dataset of chest X-rays with radiologist's annotations

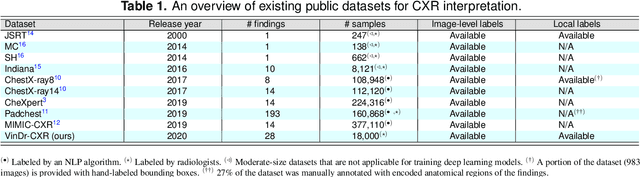
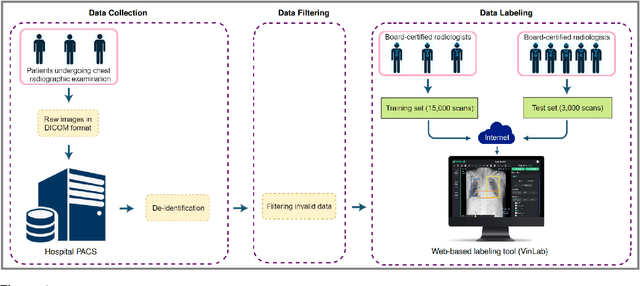
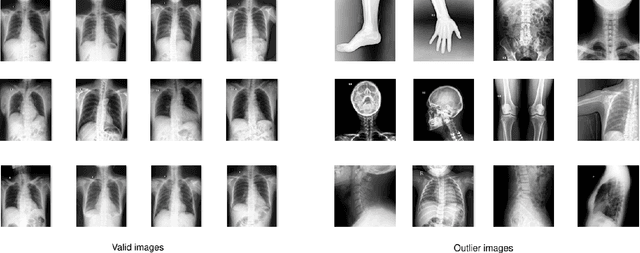
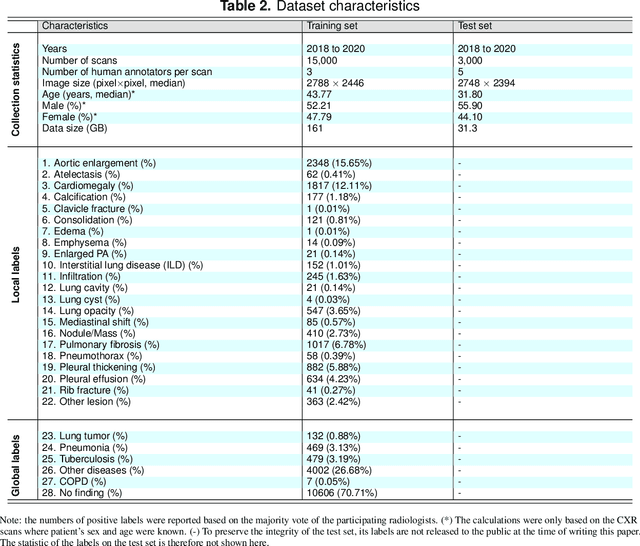
Most of the existing chest X-ray datasets include labels from a list of findings without specifying their locations on the radiographs. This limits the development of machine learning algorithms for the detection and localization of chest abnormalities. In this work, we describe a dataset of more than 100,000 chest X-ray scans that were retrospectively collected from two major hospitals in Vietnam. Out of this raw data, we release 18,000 images that were manually annotated by a total of 17 experienced radiologists with 22 local labels of rectangles surrounding abnormalities and 6 global labels of suspected diseases. The released dataset is divided into a training set of 15,000 and a test set of 3,000. Each scan in the training set was independently labeled by 3 radiologists, while each scan in the test set was labeled by the consensus of 5 radiologists. We designed and built a labeling platform for DICOM images to facilitate these annotation procedures. All images are made publicly available in DICOM format in company with the labels of the training set. The labels of the test set are hidden at the time of writing this paper as they will be used for benchmarking machine learning algorithms on an open platform.

Random perturbation and matrix sparsification and completion

We discuss general perturbation inequalities when the perturbation is random. As applications, we obtain several new results concerning two important problems: matrix sparsification and matrix completion.