Vaishnavi Gupta
Non-Stochastic CDF Estimation Using Threshold Queries
Jan 13, 2023Abstract:Estimating the empirical distribution of a scalar-valued data set is a basic and fundamental task. In this paper, we tackle the problem of estimating an empirical distribution in a setting with two challenging features. First, the algorithm does not directly observe the data; instead, it only asks a limited number of threshold queries about each sample. Second, the data are not assumed to be independent and identically distributed; instead, we allow for an arbitrary process generating the samples, including an adaptive adversary. These considerations are relevant, for example, when modeling a seller experimenting with posted prices to estimate the distribution of consumers' willingness to pay for a product: offering a price and observing a consumer's purchase decision is equivalent to asking a single threshold query about their value, and the distribution of consumers' values may be non-stationary over time, as early adopters may differ markedly from late adopters. Our main result quantifies, to within a constant factor, the sample complexity of estimating the empirical CDF of a sequence of elements of $[n]$, up to $\varepsilon$ additive error, using one threshold query per sample. The complexity depends only logarithmically on $n$, and our result can be interpreted as extending the existing logarithmic-complexity results for noisy binary search to the more challenging setting where noise is non-stochastic. Along the way to designing our algorithm, we consider a more general model in which the algorithm is allowed to make a limited number of simultaneous threshold queries on each sample. We solve this problem using Blackwell's Approachability Theorem and the exponential weights method. As a side result of independent interest, we characterize the minimum number of simultaneous threshold queries required by deterministic CDF estimation algorithms.
Large Scale Learning on Non-Homophilous Graphs: New Benchmarks and Strong Simple Methods
Oct 27, 2021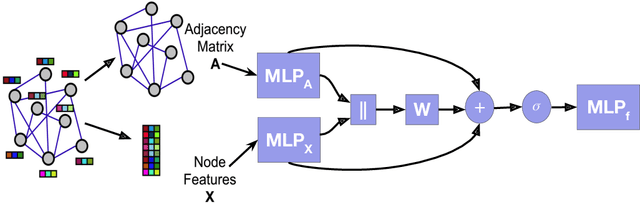
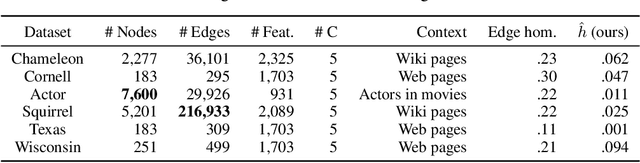
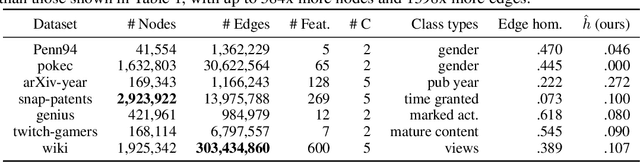
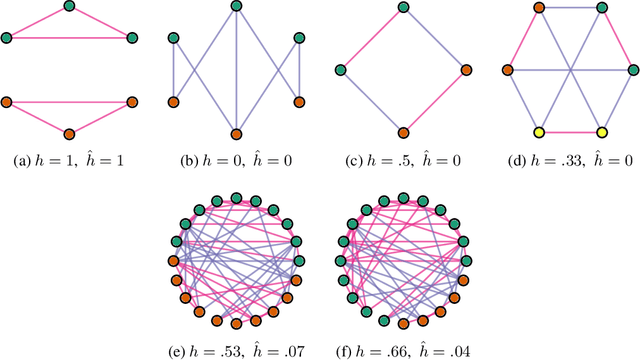
Abstract:Many widely used datasets for graph machine learning tasks have generally been homophilous, where nodes with similar labels connect to each other. Recently, new Graph Neural Networks (GNNs) have been developed that move beyond the homophily regime; however, their evaluation has often been conducted on small graphs with limited application domains. We collect and introduce diverse non-homophilous datasets from a variety of application areas that have up to 384x more nodes and 1398x more edges than prior datasets. We further show that existing scalable graph learning and graph minibatching techniques lead to performance degradation on these non-homophilous datasets, thus highlighting the need for further work on scalable non-homophilous methods. To address these concerns, we introduce LINKX -- a strong simple method that admits straightforward minibatch training and inference. Extensive experimental results with representative simple methods and GNNs across our proposed datasets show that LINKX achieves state-of-the-art performance for learning on non-homophilous graphs. Our codes and data are available at https://github.com/CUAI/Non-Homophily-Large-Scale.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge