Longer is (Not Necessarily) Stronger: Punctuated Long-Sequence Training for Enhanced Speech Recognition and Translation

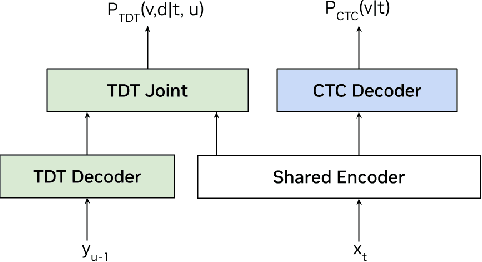
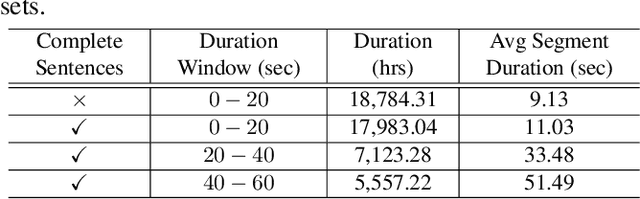
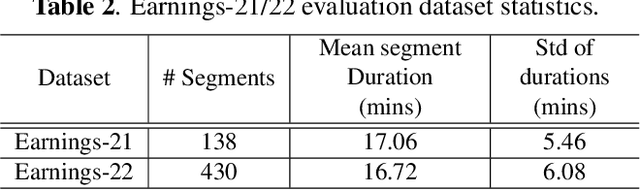
This paper presents a new method for training sequence-to-sequence models for speech recognition and translation tasks. Instead of the traditional approach of training models on short segments containing only lowercase or partial punctuation and capitalization (PnC) sentences, we propose training on longer utterances that include complete sentences with proper punctuation and capitalization. We achieve this by using the FastConformer architecture which allows training 1 Billion parameter models with sequences up to 60 seconds long with full attention. However, while training with PnC enhances the overall performance, we observed that accuracy plateaus when training on sequences longer than 40 seconds across various evaluation settings. Our proposed method significantly improves punctuation and capitalization accuracy, showing a 25% relative word error rate (WER) improvement on the Earnings-21 and Earnings-22 benchmarks. Additionally, training on longer audio segments increases the overall model accuracy across speech recognition and translation benchmarks. The model weights and training code are open-sourced though NVIDIA NeMo.

Contrastive Hebbian Learning with Random Feedback Weights

Neural networks are commonly trained to make predictions through learning algorithms. Contrastive Hebbian learning, which is a powerful rule inspired by gradient backpropagation, is based on Hebb's rule and the contrastive divergence algorithm. It operates in two phases, the forward (or free) phase, where the data are fed to the network, and a backward (or clamped) phase, where the target signals are clamped to the output layer of the network and the feedback signals are transformed through the transpose synaptic weight matrices. This implies symmetries at the synaptic level, for which there is no evidence in the brain. In this work, we propose a new variant of the algorithm, called random contrastive Hebbian learning, which does not rely on any synaptic weights symmetries. Instead, it uses random matrices to transform the feedback signals during the clamped phase, and the neural dynamics are described by first order non-linear differential equations. The algorithm is experimentally verified by solving a Boolean logic task, classification tasks (handwritten digits and letters), and an autoencoding task. This article also shows how the parameters affect learning, especially the random matrices. We use the pseudospectra analysis to investigate further how random matrices impact the learning process. Finally, we discuss the biological plausibility of the proposed algorithm, and how it can give rise to better computational models for learning.