Unsupervised Machine Learning for Detecting and Locating Human-Made Objects in 3D Point Cloud

A 3D point cloud is an unstructured, sparse, and irregular dataset, typically collected by airborne LiDAR systems over a geological region. Laser pulses emitted from these systems reflect off objects both on and above the ground, resulting in a dataset containing the longitude, latitude, and elevation of each point, as well as information about the corresponding laser pulse strengths. A widely studied research problem, addressed in many previous works, is ground filtering, which involves partitioning the points into ground and non-ground subsets. This research introduces a novel task: detecting and identifying human-made objects amidst natural tree structures. This task is performed on the subset of non-ground points derived from the ground filtering stage. Marked Point Fields (MPFs) are used as models well-suited to these tasks. The proposed methodology consists of three stages: ground filtering, local information extraction (LIE), and clustering. In the ground filtering stage, a statistical method called One-Sided Regression (OSR) is introduced, addressing the limitations of prior ground filtering methods on uneven terrains. In the LIE stage, unsupervised learning methods are lacking. To mitigate this, a kernel-based method for the Hessian matrix of the MPF is developed. In the clustering stage, the Gaussian Mixture Model (GMM) is applied to the results of the LIE stage to partition the non-ground points into trees and human-made objects. The underlying assumption is that LiDAR points from trees exhibit a three-dimensional distribution, while those from human-made objects follow a two-dimensional distribution. The Hessian matrix of the MPF effectively captures this distinction. Experimental results demonstrate that the proposed ground filtering method outperforms previous techniques, and the LIE method successfully distinguishes between points representing trees and human-made objects.

Asymptotics for The $k$-means

The $k$-means is one of the most important unsupervised learning techniques in statistics and computer science. The goal is to partition a data set into many clusters, such that observations within clusters are the most homogeneous and observations between clusters are the most heterogeneous. Although it is well known, the investigation of the asymptotic properties is far behind, leading to difficulties in developing more precise $k$-means methods in practice. To address this issue, a new concept called clustering consistency is proposed. Fundamentally, the proposed clustering consistency is more appropriate than the previous criterion consistency for the clustering methods. Using this concept, a new $k$-means method is proposed. It is found that the proposed $k$-means method has lower clustering error rates and is more robust to small clusters and outliers than existing $k$-means methods. When $k$ is unknown, using the Gap statistics, the proposed method can also identify the number of clusters. This is rarely achieved by existing $k$-means methods adopted by many software packages.

Multiple Learning for Regression in big data

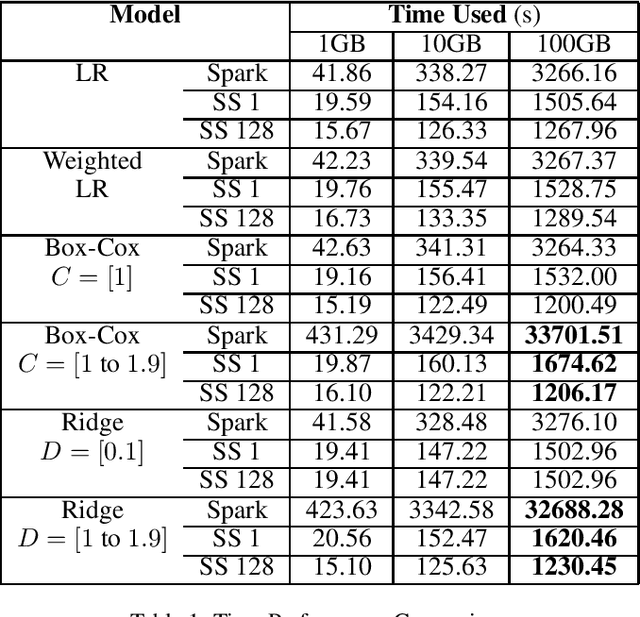
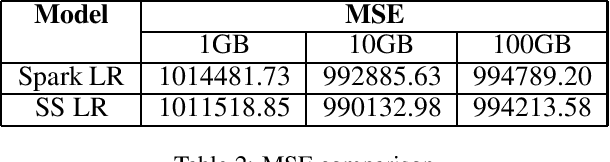
Regression problems that have closed-form solutions are well understood and can be easily implemented when the dataset is small enough to be all loaded into the RAM. Challenges arise when data is too big to be stored in RAM to compute the closed form solutions. Many techniques were proposed to overcome or alleviate the memory barrier problem but the solutions are often local optimal. In addition, most approaches require accessing the raw data again when updating the models. Parallel computing clusters are also expected if multiple models need to be computed simultaneously. We propose multiple learning approaches that utilize an array of sufficient statistics (SS) to address this big data challenge. This memory oblivious approach breaks the memory barrier when computing regressions with closed-form solutions, including but not limited to linear regression, weighted linear regression, linear regression with Box-Cox transformation (Box-Cox regression) and ridge regression models. The computation and update of the SS array can be handled at per row level or per mini-batch level. And updating a model is as easy as matrix addition and subtraction. Furthermore, multiple SS arrays for different models can be easily computed simultaneously to obtain multiple models at one pass through the dataset. We implemented our approaches on Spark and evaluated over the simulated datasets. Results showed our approaches can achieve closed-form solutions of multiple models at the cost of half training time of the traditional methods for a single model.