What is the $\textit{intrinsic}$ dimension of your binary data? -- and how to compute it quickly

Dimensionality is an important aspect for analyzing and understanding (high-dimensional) data. In their 2006 ICDM paper Tatti et al. answered the question for a (interpretable) dimension of binary data tables by introducing a normalized correlation dimension. In the present work we revisit their results and contrast them with a concept based notion of intrinsic dimension (ID) recently introduced for geometric data sets. To do this, we present a novel approximation for this ID that is based on computing concepts only up to a certain support value. We demonstrate and evaluate our approximation using all available datasets from Tatti et al., which have between 469 and 41271 extrinsic dimensions.

A Repository for Formal Contexts

Data is always at the center of the theoretical development and investigation of the applicability of formal concept analysis. It is therefore not surprising that a large number of data sets are repeatedly used in scholarly articles and software tools, acting as de facto standard data sets. However, the distribution of the data sets poses a problem for the sustainable development of the research field. There is a lack of a central location that provides and describes FCA data sets and links them to already known analysis results. This article analyses the current state of the dissemination of FCA data sets, presents the requirements for a central FCA repository, and highlights the challenges for this.

Reproducibility and Geometric Intrinsic Dimensionality: An Investigation on Graph Neural Network Research

Difficulties in replication and reproducibility of empirical evidences in machine learning research have become a prominent topic in recent years. Ensuring that machine learning research results are sound and reliable requires reproducibility, which verifies the reliability of research findings using the same code and data. This promotes open and accessible research, robust experimental workflows, and the rapid integration of new findings. Evaluating the degree to which research publications support these different aspects of reproducibility is one goal of the present work. For this we introduce an ontology of reproducibility in machine learning and apply it to methods for graph neural networks. Building on these efforts we turn towards another critical challenge in machine learning, namely the curse of dimensionality, which poses challenges in data collection, representation, and analysis, making it harder to find representative data and impeding the training and inference processes. Using the closely linked concept of geometric intrinsic dimension we investigate to which extend the used machine learning models are influenced by the intrinsic dimension of the data sets they are trained on.

The Geometric Structure of Topic Models

Topic models are a popular tool for clustering and analyzing textual data. They allow texts to be classified on the basis of their affiliation to the previously calculated topics. Despite their widespread use in research and application, an in-depth analysis of topic models is still an open research topic. State-of-the-art methods for interpreting topic models are based on simple visualizations, such as similarity matrices, top-term lists or embeddings, which are limited to a maximum of three dimensions. In this paper, we propose an incidence-geometric method for deriving an ordinal structure from flat topic models, such as non-negative matrix factorization. These enable the analysis of the topic model in a higher (order) dimension and the possibility of extracting conceptual relationships between several topics at once. Due to the use of conceptual scaling, our approach does not introduce any artificial topical relationships, such as artifacts of feature compression. Based on our findings, we present a new visualization paradigm for concept hierarchies based on ordinal motifs. These allow for a top-down view on topic spaces. We introduce and demonstrate the applicability of our approach based on a topic model derived from a corpus of scientific papers taken from 32 top machine learning venues.

Towards Ordinal Data Science

Order is one of the main instruments to measure the relationship between objects in (empirical) data. However, compared to methods that use numerical properties of objects, the amount of ordinal methods developed is rather small. One reason for this is the limited availability of computational resources in the last century that would have been required for ordinal computations. Another reason -- particularly important for this line of research -- is that order-based methods are often seen as too mathematically rigorous for applying them to real-world data. In this paper, we will therefore discuss different means for measuring and 'calculating' with ordinal structures -- a specific class of directed graphs -- and show how to infer knowledge from them. Our aim is to establish Ordinal Data Science as a fundamentally new research agenda. Besides cross-fertilization with other cornerstone machine learning and knowledge representation methods, a broad range of disciplines will benefit from this endeavor, including, psychology, sociology, economics, web science, knowledge engineering, scientometrics.

Automatic Textual Explanations of Concept Lattices

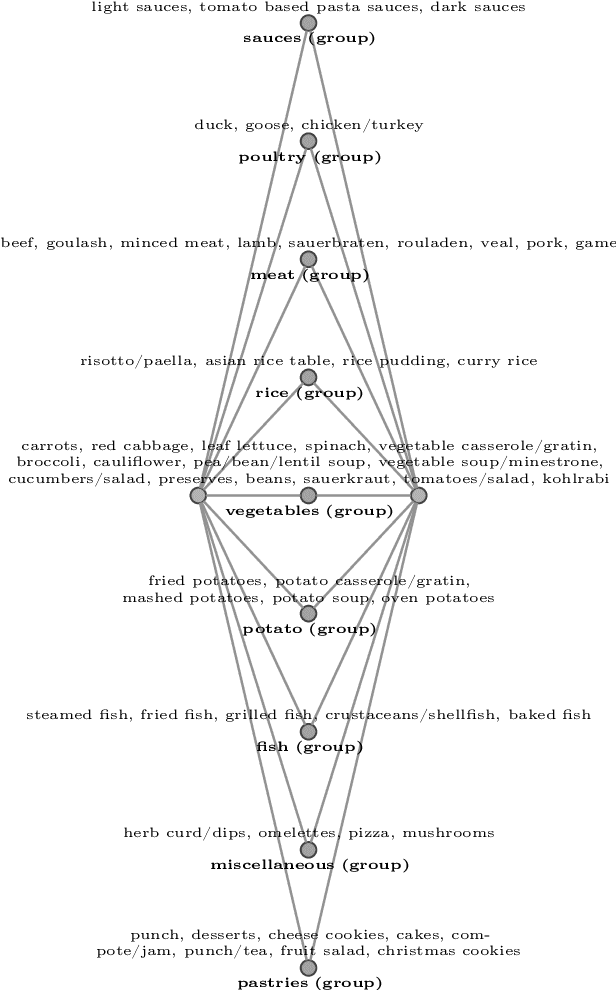
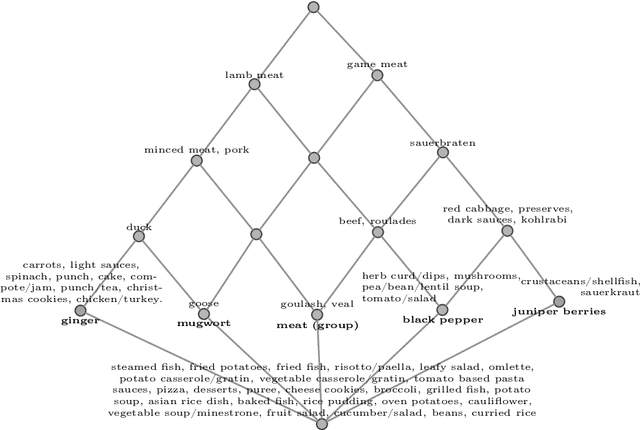
Lattices and their order diagrams are an essential tool for communicating knowledge and insights about data. This is in particular true when applying Formal Concept Analysis. Such representations, however, are difficult to comprehend by untrained users and in general in cases where lattices are large. We tackle this problem by automatically generating textual explanations for lattices using standard scales. Our method is based on the general notion of ordinal motifs in lattices for the special case of standard scales. We show the computational complexity of identifying a small number of standard scales that cover most of the lattice structure. For these, we provide textual explanation templates, which can be applied to any occurrence of a scale in any data domain. These templates are derived using principles from human-computer interaction and allow for a comprehensive textual explanation of lattices. We demonstrate our approach on the spices planner data set, which is a medium sized formal context comprised of fifty-six meals (objects) and thirty-seven spices (attributes). The resulting 531 formal concepts can be covered by means of about 100 standard scales.

Selecting Features by their Resilience to the Curse of Dimensionality

Real-world datasets are often of high dimension and effected by the curse of dimensionality. This hinders their comprehensibility and interpretability. To reduce the complexity feature selection aims to identify features that are crucial to learn from said data. While measures of relevance and pairwise similarities are commonly used, the curse of dimensionality is rarely incorporated into the process of selecting features. Here we step in with a novel method that identifies the features that allow to discriminate data subsets of different sizes. By adapting recent work on computing intrinsic dimensionalities, our method is able to select the features that can discriminate data and thus weaken the curse of dimensionality. Our experiments show that our method is competitive and commonly outperforms established feature selection methods. Furthermore, we propose an approximation that allows our method to scale to datasets consisting of millions of data points. Our findings suggest that features that discriminate data and are connected to a low intrinsic dimensionality are meaningful for learning procedures.

Ordinal Motifs in Lattices

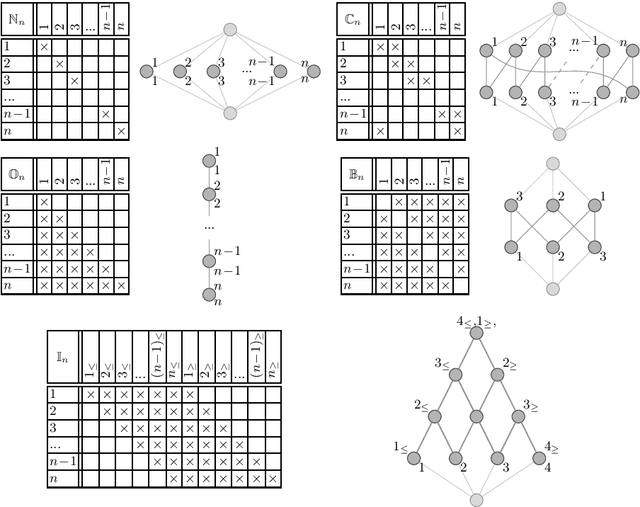
Lattices are a commonly used structure for the representation and analysis of relational and ontological knowledge. In particular, the analysis of these requires a decomposition of a large and high-dimensional lattice into a set of understandably large parts. With the present work we propose /ordinal motifs/ as analytical units of meaning. We study these ordinal substructures (or standard scales) through (full) scale-measures of formal contexts from the field of formal concept analysis. We show that the underlying decision problems are NP-complete and provide results on how one can incrementally identify ordinal motifs to save computational effort. Accompanying our theoretical results, we demonstrate how ordinal motifs can be leveraged to retrieve basic meaning from a medium sized ordinal data set.

Scaling Dimension

Conceptual Scaling is a useful standard tool in Formal Concept Analysis and beyond. Its mathematical theory, as elaborated in the last chapter of the FCA monograph, still has room for improvement. As it stands, even some of the basic definitions are in flux. Our contribution was triggered by the study of concept lattices for tree classifiers and the scaling methods used there. We extend some basic notions, give precise mathematical definitions for them and introduce the concept of scaling dimension. In addition to a detailed discussion of its properties, including an example, we show theoretical bounds related to the order dimension of concept lattices. We also study special subclasses, such as the ordinal and the interordinal scaling dimensions, and show for them first results and examples.

Conceptual Views on Tree Ensemble Classifiers

Random Forests and related tree-based methods are popular for supervised learning from table based data. Apart from their ease of parallelization, their classification performance is also superior. However, this performance, especially parallelizability, is offset by the loss of explainability. Statistical methods are often used to compensate for this disadvantage. Yet, their ability for local explanations, and in particular for global explanations, is limited. In the present work we propose an algebraic method, rooted in lattice theory, for the (global) explanation of tree ensembles. In detail, we introduce two novel conceptual views on tree ensemble classifiers and demonstrate their explanatory capabilities on Random Forests that were trained with standard parameters.