Conceptual Mapping of Controversies

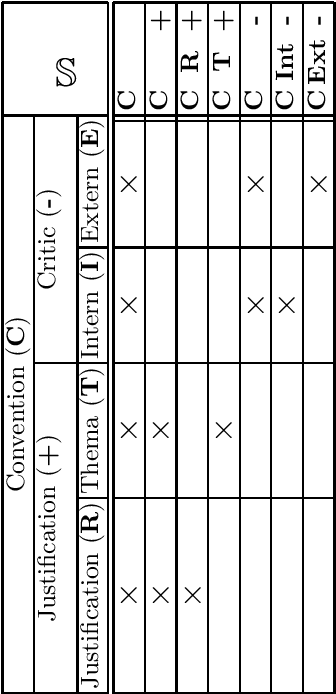
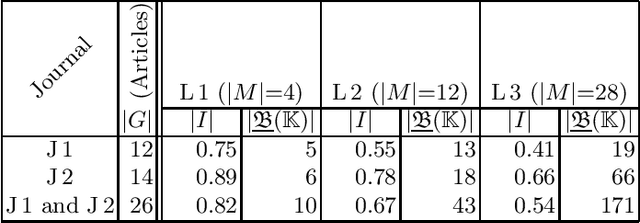
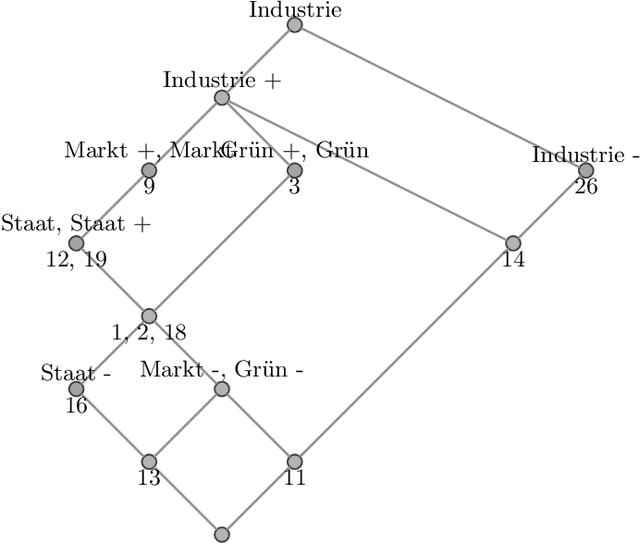
With our work, we contribute towards a qualitative analysis of the discourse on controversies in online news media. For this, we employ Formal Concept Analysis and the economics of conventions to derive conceptual controversy maps. In our experiments, we analyze two maps from different news journals with methods from ordinal data science. We show how these methods can be used to assess the diversity, complexity and potential bias of controversies. In addition to that, we discuss how the diagrams of concept lattices can be used to navigate between news articles.

Towards Ordinal Data Science

Order is one of the main instruments to measure the relationship between objects in (empirical) data. However, compared to methods that use numerical properties of objects, the amount of ordinal methods developed is rather small. One reason for this is the limited availability of computational resources in the last century that would have been required for ordinal computations. Another reason -- particularly important for this line of research -- is that order-based methods are often seen as too mathematically rigorous for applying them to real-world data. In this paper, we will therefore discuss different means for measuring and 'calculating' with ordinal structures -- a specific class of directed graphs -- and show how to infer knowledge from them. Our aim is to establish Ordinal Data Science as a fundamentally new research agenda. Besides cross-fertilization with other cornerstone machine learning and knowledge representation methods, a broad range of disciplines will benefit from this endeavor, including, psychology, sociology, economics, web science, knowledge engineering, scientometrics.

Maximal Ordinal Two-Factorizations

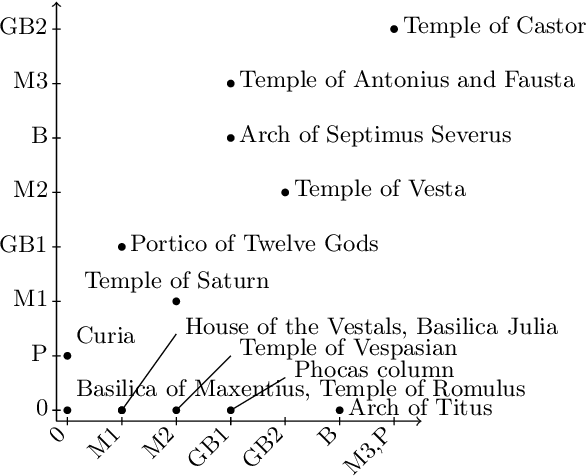
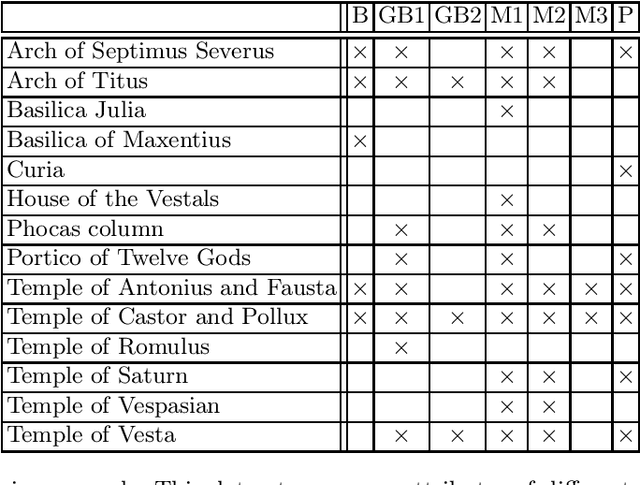
Given a formal context, an ordinal factor is a subset of its incidence relation that forms a chain in the concept lattice, i.e., a part of the dataset that corresponds to a linear order. To visualize the data in a formal context, Ganter and Glodeanu proposed a biplot based on two ordinal factors. For the biplot to be useful, it is important that these factors comprise as much data points as possible, i.e., that they cover a large part of the incidence relation. In this work, we investigate such ordinal two-factorizations. First, we investigate for formal contexts that omit ordinal two-factorizations the disjointness of the two factors. Then, we show that deciding on the existence of two-factorizations of a given size is an NP-complete problem which makes computing maximal factorizations computationally expensive. Finally, we provide the algorithm Ord2Factor that allows us to compute large ordinal two-factorizations.

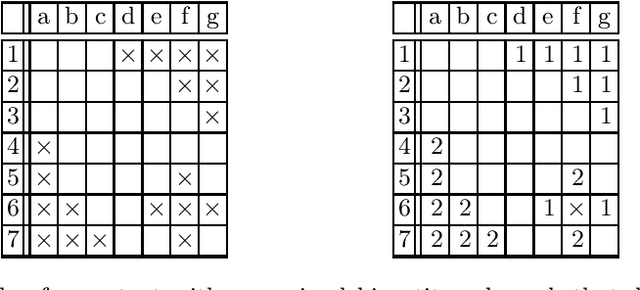
Greedy Discovery of Ordinal Factors

In large datasets, it is hard to discover and analyze structure. It is thus common to introduce tags or keywords for the items. In applications, such datasets are then filtered based on these tags. Still, even medium-sized datasets with a few tags result in complex and for humans hard-to-navigate systems. In this work, we adopt the method of ordinal factor analysis to address this problem. An ordinal factor arranges a subset of the tags in a linear order based on their underlying structure. A complete ordinal factorization, which consists of such ordinal factors, precisely represents the original dataset. Based on such an ordinal factorization, we provide a way to discover and explain relationships between different items and attributes in the dataset. However, computing even just one ordinal factor of high cardinality is computationally complex. We thus propose the greedy algorithm in this work. This algorithm extracts ordinal factors using already existing fast algorithms developed in formal concept analysis. Then, we leverage to propose a comprehensive way to discover relationships in the dataset. We furthermore introduce a distance measure based on the representation emerging from the ordinal factorization to discover similar items. To evaluate the method, we conduct a case study on different datasets.

Discovering Locally Maximal Bipartite Subgraphs

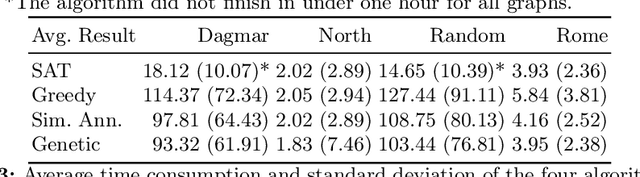
Induced bipartite subgraphs of maximal vertex cardinality are an essential concept for the analysis of graphs. Yet, discovering them in large graphs is known to be computationally hard. Therefore, we consider in this work a weaker notion of this problem, where we discard the maximality constraint in favor of inclusion maximality. Thus, we aim to discover locally maximal bipartite subgraphs. For this, we present three heuristic approaches to extract such subgraphs and compare their results to the solutions of the global problem. For the latter, we employ the algorithmic strength of fast SAT-solvers. Our three proposed heuristics are based on a greedy strategy, a simulated annealing approach, and a genetic algorithm, respectively. We evaluate all four algorithms with respect to their time requirement and the vertex cardinality of the discovered bipartite subgraphs on several benchmark datasets

Attribute Selection using Contranominal Scales

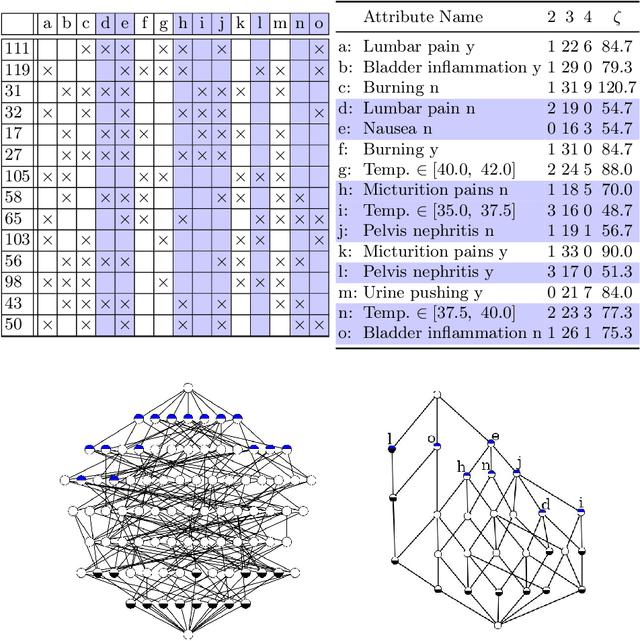
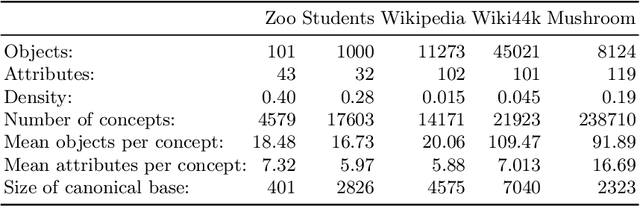
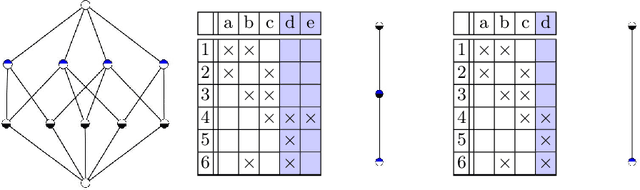
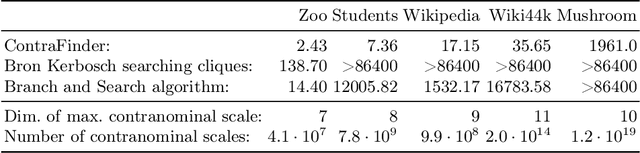
Formal Concept Analysis (FCA) allows to analyze binary data by deriving concepts and ordering them in lattices. One of the main goals of FCA is to enable humans to comprehend the information that is encapsulated in the data; however, the large size of concept lattices is a limiting factor for the feasibility of understanding the underlying structural properties. The size of such a lattice depends on the number of subcontexts in the corresponding formal context that are isomorphic to a contranominal scale of high dimension. In this work, we propose the algorithm ContraFinder that enables the computation of all contranominal scales of a given formal context. Leveraging this algorithm, we introduce delta-adjusting, a novel approach in order to decrease the number of contranominal scales in a formal context by the selection of an appropriate attribute subset. We demonstrate that delta-adjusting a context reduces the size of the hereby emerging sub-semilattice and that the implication set is restricted to meaningful implications. This is evaluated with respect to its associated knowledge by means of a classification task. Hence, our proposed technique strongly improves understandability while preserving important conceptual structures.

Neural Networks for Semantic Gaze Analysis in XR Settings

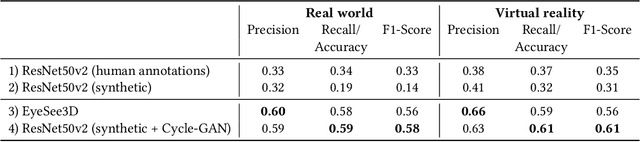
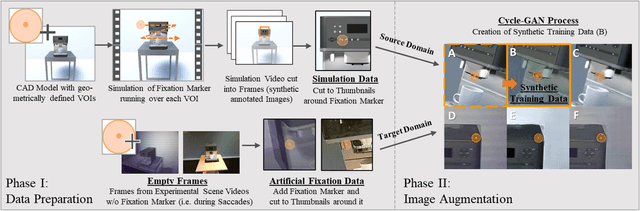
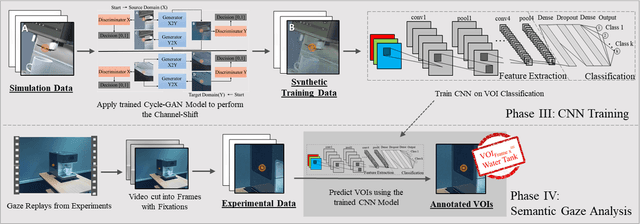
Virtual-reality (VR) and augmented-reality (AR) technology is increasingly combined with eye-tracking. This combination broadens both fields and opens up new areas of application, in which visual perception and related cognitive processes can be studied in interactive but still well controlled settings. However, performing a semantic gaze analysis of eye-tracking data from interactive three-dimensional scenes is a resource-intense task, which so far has been an obstacle to economic use. In this paper we present a novel approach which minimizes time and information necessary to annotate volumes of interest (VOIs) by using techniques from object recognition. To do so, we train convolutional neural networks (CNNs) on synthetic data sets derived from virtual models using image augmentation techniques. We evaluate our method in real and virtual environments, showing that the method can compete with state-of-the-art approaches, while not relying on additional markers or preexisting databases but instead offering cross-platform use.

FCA2VEC: Embedding Techniques for Formal Concept Analysis

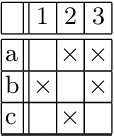
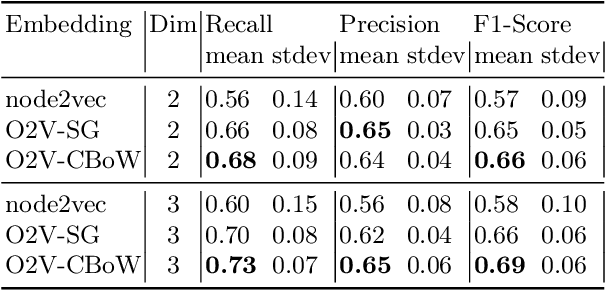
Embedding large and high dimensional data into low dimensional vector spaces is a necessary task to computationally cope with contemporary data sets. Superseding latent semantic analysis recent approaches like word2vec or node2vec are well established tools in this realm. In the present paper we add to this line of research by introducing fca2vec, a family of embedding techniques for formal concept analysis (FCA). Our investigation contributes to two distinct lines of research. First, we enable the application of FCA notions to large data sets. In particular, we demonstrate how the cover relation of a concept lattice can be retrieved from a computational feasible embedding. Secondly, we show an enhancement for the classical node2vec approach in low dimension. For both directions the overall constraint of FCA of explainable results is preserved. We evaluate our novel procedures by computing fca2vec on different data sets like, wiki44 (a dense part of the Wikidata knowledge graph), the Mushroom data set and a publication network derived from the FCA community.

DimDraw -- A novel tool for drawing concept lattices

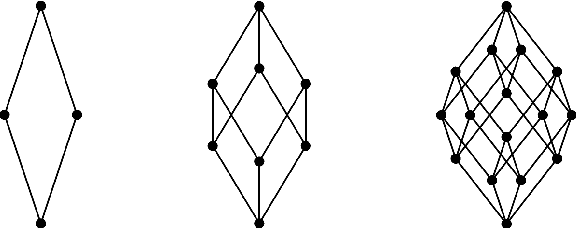
Concept lattice drawings are an important tool to visualize complex relations in data in a simple manner to human readers. Many attempts were made to transfer classical graph drawing approaches to order diagrams. Although those methods are satisfying for some lattices they unfortunately perform poorly in general. In this work we present a novel tool to draw concept lattices that is purely motivated by the order structure.