Viktoria Horn
Conceptual Mapping of Controversies
Apr 25, 2024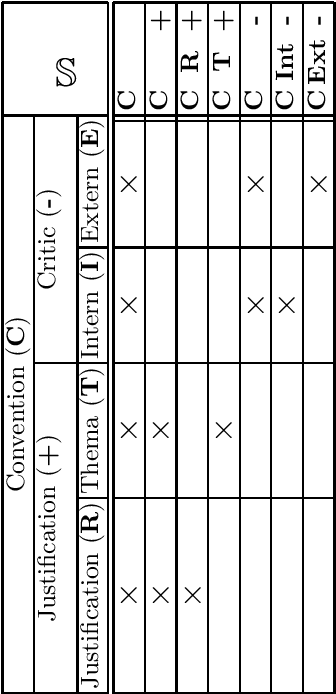
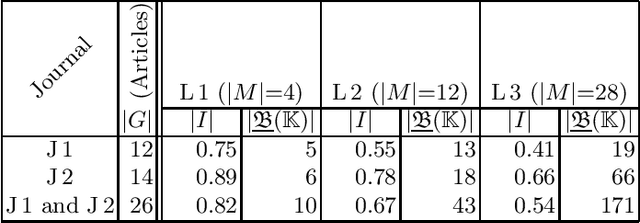
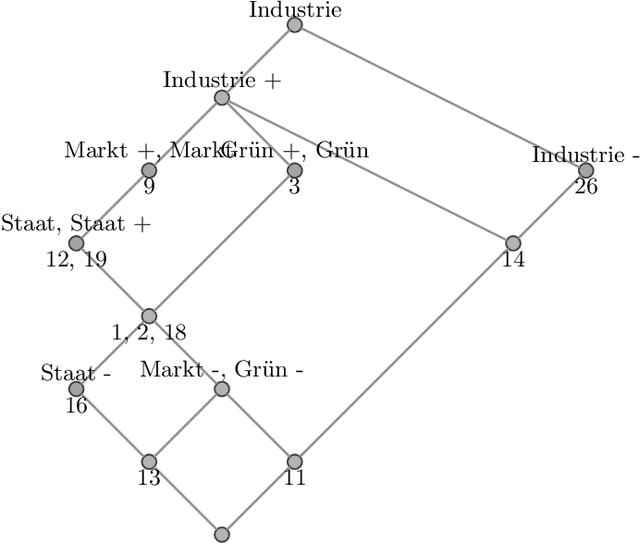

Abstract:With our work, we contribute towards a qualitative analysis of the discourse on controversies in online news media. For this, we employ Formal Concept Analysis and the economics of conventions to derive conceptual controversy maps. In our experiments, we analyze two maps from different news journals with methods from ordinal data science. We show how these methods can be used to assess the diversity, complexity and potential bias of controversies. In addition to that, we discuss how the diagrams of concept lattices can be used to navigate between news articles.
Automatic Textual Explanations of Concept Lattices
Apr 17, 2023Abstract:Lattices and their order diagrams are an essential tool for communicating knowledge and insights about data. This is in particular true when applying Formal Concept Analysis. Such representations, however, are difficult to comprehend by untrained users and in general in cases where lattices are large. We tackle this problem by automatically generating textual explanations for lattices using standard scales. Our method is based on the general notion of ordinal motifs in lattices for the special case of standard scales. We show the computational complexity of identifying a small number of standard scales that cover most of the lattice structure. For these, we provide textual explanation templates, which can be applied to any occurrence of a scale in any data domain. These templates are derived using principles from human-computer interaction and allow for a comprehensive textual explanation of lattices. We demonstrate our approach on the spices planner data set, which is a medium sized formal context comprised of fifty-six meals (objects) and thirty-seven spices (attributes). The resulting 531 formal concepts can be covered by means of about 100 standard scales.
Ordinal Motifs in Lattices
Apr 10, 2023Abstract:Lattices are a commonly used structure for the representation and analysis of relational and ontological knowledge. In particular, the analysis of these requires a decomposition of a large and high-dimensional lattice into a set of understandably large parts. With the present work we propose /ordinal motifs/ as analytical units of meaning. We study these ordinal substructures (or standard scales) through (full) scale-measures of formal contexts from the field of formal concept analysis. We show that the underlying decision problems are NP-complete and provide results on how one can incrementally identify ordinal motifs to save computational effort. Accompanying our theoretical results, we demonstrate how ordinal motifs can be leveraged to retrieve basic meaning from a medium sized ordinal data set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge