Maren Koyda
Attribute Selection using Contranominal Scales
Jul 01, 2021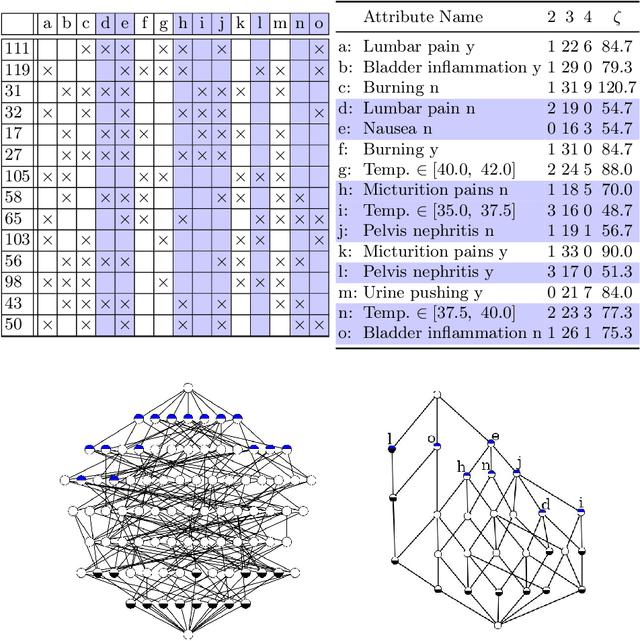
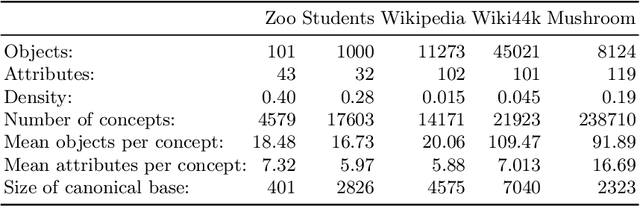
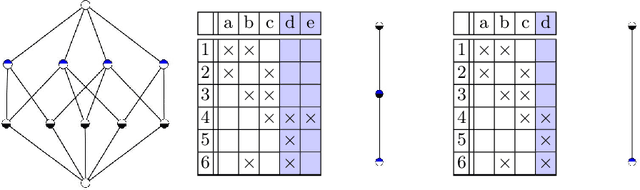
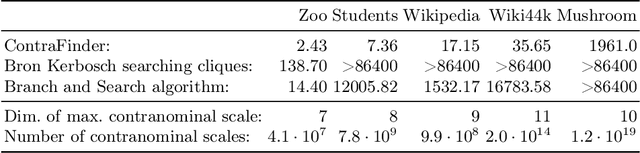
Abstract:Formal Concept Analysis (FCA) allows to analyze binary data by deriving concepts and ordering them in lattices. One of the main goals of FCA is to enable humans to comprehend the information that is encapsulated in the data; however, the large size of concept lattices is a limiting factor for the feasibility of understanding the underlying structural properties. The size of such a lattice depends on the number of subcontexts in the corresponding formal context that are isomorphic to a contranominal scale of high dimension. In this work, we propose the algorithm ContraFinder that enables the computation of all contranominal scales of a given formal context. Leveraging this algorithm, we introduce delta-adjusting, a novel approach in order to decrease the number of contranominal scales in a formal context by the selection of an appropriate attribute subset. We demonstrate that delta-adjusting a context reduces the size of the hereby emerging sub-semilattice and that the implication set is restricted to meaningful implications. This is evaluated with respect to its associated knowledge by means of a classification task. Hence, our proposed technique strongly improves understandability while preserving important conceptual structures.
Relevant Attributes in Formal Contexts
Dec 20, 2018

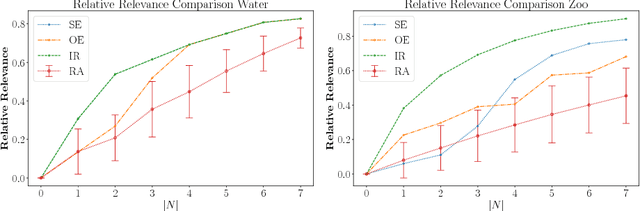

Abstract:Computing conceptual structures, like formal concept lattices, is in the age of massive data sets a challenging task. There are various approaches to deal with this, e.g., random sampling, parallelization, or attribute extraction. A so far not investigated method in the realm of formal concept analysis is attribute selection, as done in machine learning. Building up on this we introduce a method for attribute selection in formal contexts. To this end, we propose the notion of relevant attributes which enables us to define a relative relevance function, reflecting both the order structure of the concept lattice as well as distribution of objects on it. Finally, we overcome computational challenges for computing the relative relevance through an approximation approach based on information entropy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge