Tinu Theckel Joy
Analyzing Epistemic and Aleatoric Uncertainty for Drusen Segmentation in Optical Coherence Tomography Images
Feb 08, 2021
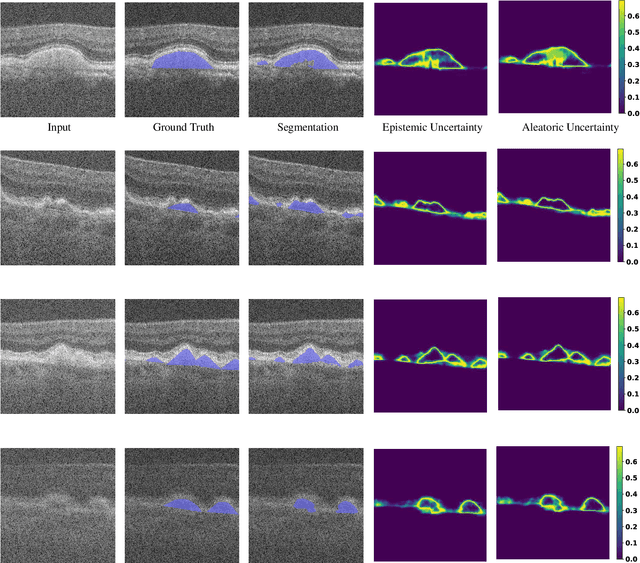
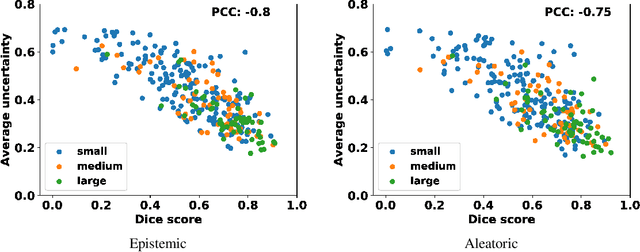
Abstract:Age-related macular degeneration (AMD) is one of the leading causes of permanent vision loss in people aged over 60 years. Accurate segmentation of biomarkers such as drusen that points to the early stages of AMD is crucial in preventing further vision impairment. However, segmenting drusen is extremely challenging due to their varied sizes and appearances, low contrast and noise resemblance. Most existing literature, therefore, have focused on size estimation of drusen using classification, leaving the challenge of accurate segmentation less tackled. Additionally, obtaining the pixel-wise annotations is extremely costly and such labels can often be noisy, suffering from inter-observer and intra-observer variability. Quantification of uncertainty associated with segmentation tasks offers principled measures to inspect the segmentation output. Realizing its utility in identifying erroneous segmentation and the potential applications in clinical decision making, here we develop a U-Net based drusen segmentation model and quantify the segmentation uncertainty. We investigate epistemic and aleatoric uncertainty capturing model confidence and data uncertainty respectively. We present segmentation results and show how uncertainty can help formulate robust evaluation strategies. We visually inspect the pixel-wise uncertainty and segmentation results on test images. We finally analyze the correlation between segmentation uncertainty and accuracy. Our results demonstrate the utility of leveraging uncertainties in developing and explaining segmentation models for medical image analysis.
Fast Hyperparameter Tuning using Bayesian Optimization with Directional Derivatives
Feb 06, 2019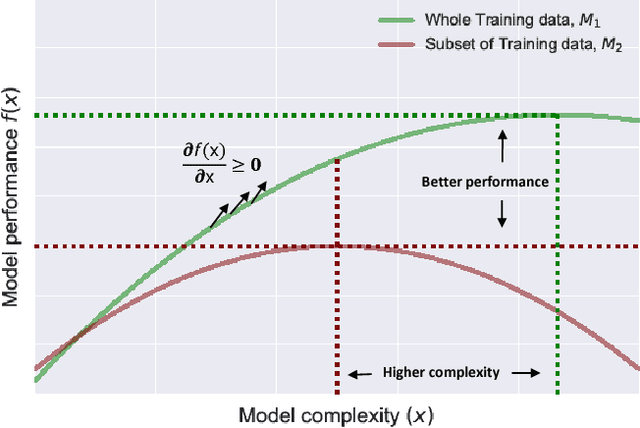



Abstract:In this paper we develop a Bayesian optimization based hyperparameter tuning framework inspired by statistical learning theory for classifiers. We utilize two key facts from PAC learning theory; the generalization bound will be higher for a small subset of data compared to the whole, and the highest accuracy for a small subset of data can be achieved with a simple model. We initially tune the hyperparameters on a small subset of training data using Bayesian optimization. While tuning the hyperparameters on the whole training data, we leverage the insights from the learning theory to seek more complex models. We realize this by using directional derivative signs strategically placed in the hyperparameter search space to seek a more complex model than the one obtained with small data. We demonstrate the performance of our method on the tasks of tuning the hyperparameters of several machine learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge