Efficient Approximation of Expected Hypervolume Improvement using Gauss-Hermite Quadrature

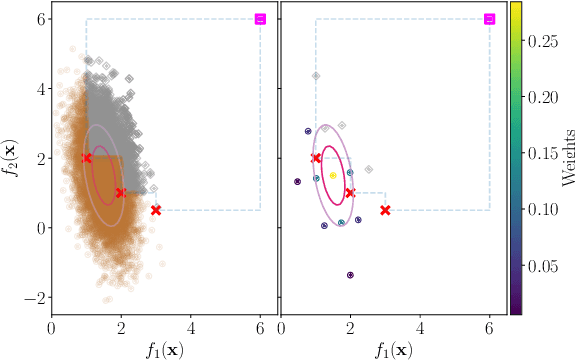
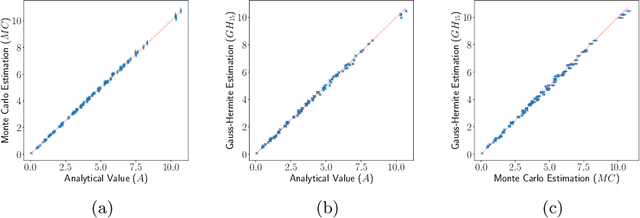
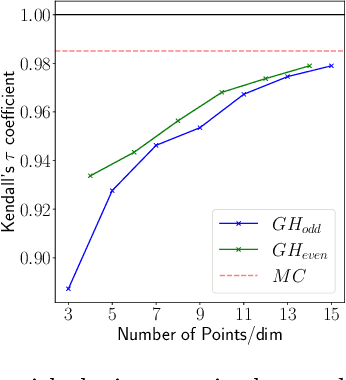
Many methods for performing multi-objective optimisation of computationally expensive problems have been proposed recently. Typically, a probabilistic surrogate for each objective is constructed from an initial dataset. The surrogates can then be used to produce predictive densities in the objective space for any solution. Using the predictive densities, we can compute the expected hypervolume improvement (EHVI) due to a solution. Maximising the EHVI, we can locate the most promising solution that may be expensively evaluated next. There are closed-form expressions for computing the EHVI, integrating over the multivariate predictive densities. However, they require partitioning the objective space, which can be prohibitively expensive for more than three objectives. Furthermore, there are no closed-form expressions for a problem where the predictive densities are dependent, capturing the correlations between objectives. Monte Carlo approximation is used instead in such cases, which is not cheap. Hence, the need to develop new accurate but cheaper approximation methods remains. Here we investigate an alternative approach toward approximating the EHVI using Gauss-Hermite quadrature. We show that it can be an accurate alternative to Monte Carlo for both independent and correlated predictive densities with statistically significant rank correlations for a range of popular test problems.

R-MBO: A Multi-surrogate Approach for Preference Incorporation in Multi-objective Bayesian Optimisation

Many real-world multi-objective optimisation problems rely on computationally expensive function evaluations. Multi-objective Bayesian optimisation (BO) can be used to alleviate the computation time to find an approximated set of Pareto optimal solutions. In many real-world problems, a decision-maker has some preferences on the objective functions. One approach to incorporate the preferences in multi-objective BO is to use a scalarising function and build a single surrogate model (mono-surrogate approach) on it. This approach has two major limitations. Firstly, the fitness landscape of the scalarising function and the objective functions may not be similar. Secondly, the approach assumes that the scalarising function distribution is Gaussian, and thus a closed-form expression of an acquisition function e.g., expected improvement can be used. We overcome these limitations by building independent surrogate models (multi-surrogate approach) on each objective function and show that the distribution of the scalarising function is not Gaussian. We approximate the distribution using Generalised value distribution. We present an a-priori multi-surrogate approach to incorporate the desirable objective function values (or reference point) as the preferences of a decision-maker in multi-objective BO. The results and comparison with the existing mono-surrogate approach on benchmark and real-world optimisation problems show the potential of the proposed approach.

Wind Farm Layout Optimisation using Set Based Multi-objective Bayesian Optimisation

Wind energy is one of the cleanest renewable electricity sources and can help in addressing the challenge of climate change. One of the drawbacks of wind-generated energy is the large space necessary to install a wind farm; this arises from the fact that placing wind turbines in a limited area would hinder their productivity and therefore not be economically convenient. This naturally leads to an optimisation problem, which has three specific challenges: (1) multiple conflicting objectives (2) computationally expensive simulation models and (3) optimisation over design sets instead of design vectors. The first and second challenges can be addressed by using surrogate-assisted e.g.\ Bayesian multi-objective optimisation. However, the traditional Bayesian optimisation cannot be applied as the optimisation function in the problem relies on design sets instead of design vectors. This paper extends the applicability of Bayesian multi-objective optimisation to set based optimisation for solving the wind farm layout problem. We use a set-based kernel in Gaussian process to quantify the correlation between wind farms (with a different number of turbines). The results on the given data set of wind energy and direction clearly show the potential of using set-based Bayesian multi-objective optimisation.

MBORE: Multi-objective Bayesian Optimisation by Density-Ratio Estimation

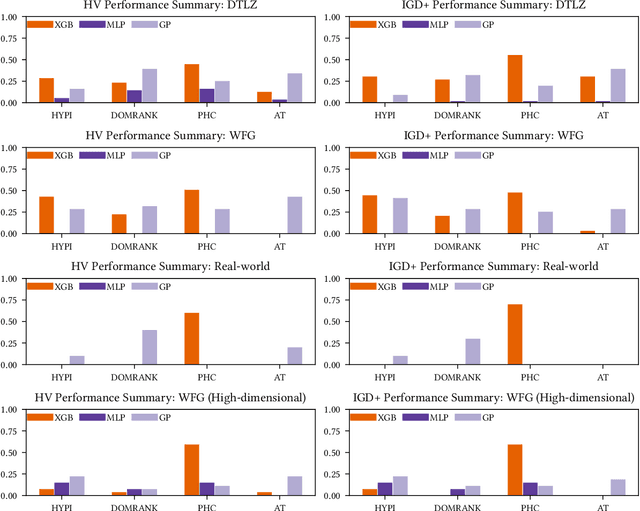
Optimisation problems often have multiple conflicting objectives that can be computationally and/or financially expensive. Mono-surrogate Bayesian optimisation (BO) is a popular model-based approach for optimising such black-box functions. It combines objective values via scalarisation and builds a Gaussian process (GP) surrogate of the scalarised values. The location which maximises a cheap-to-query acquisition function is chosen as the next location to expensively evaluate. While BO is an effective strategy, the use of GPs is limiting. Their performance decreases as the problem input dimensionality increases, and their computational complexity scales cubically with the amount of data. To address these limitations, we extend previous work on BO by density-ratio estimation (BORE) to the multi-objective setting. BORE links the computation of the probability of improvement acquisition function to that of probabilistic classification. This enables the use of state-of-the-art classifiers in a BO-like framework. In this work we present MBORE: multi-objective Bayesian optimisation by density-ratio estimation, and compare it to BO across a range of synthetic and real-world benchmarks. We find that MBORE performs as well as or better than BO on a wide variety of problems, and that it outperforms BO on high-dimensional and real-world problems.

What Makes an Effective Scalarising Function for Multi-Objective Bayesian Optimisation?

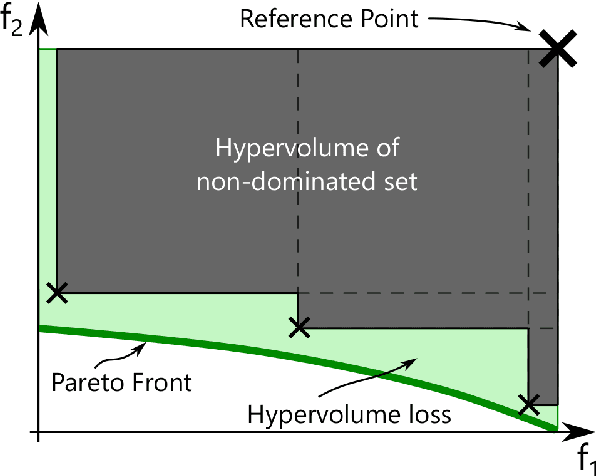
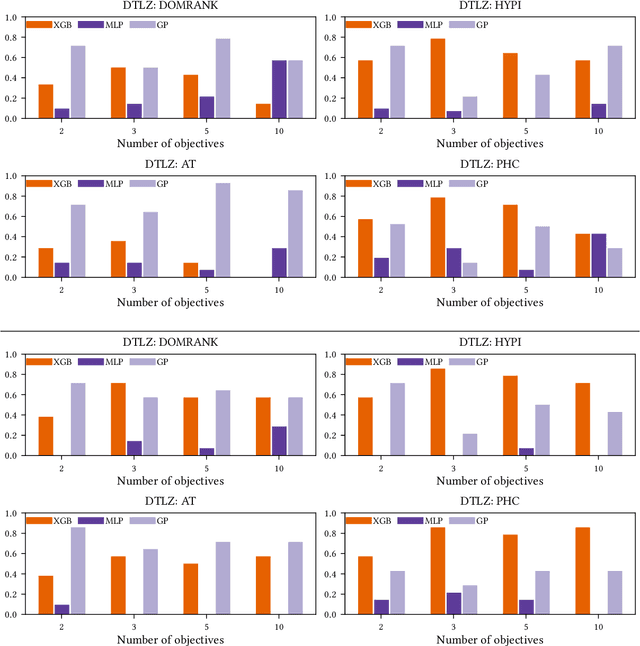
Performing multi-objective Bayesian optimisation by scalarising the objectives avoids the computation of expensive multi-dimensional integral-based acquisition functions, instead of allowing one-dimensional standard acquisition functions\textemdash such as Expected Improvement\textemdash to be applied. Here, two infill criteria based on hypervolume improvement\textemdash one recently introduced and one novel\textemdash are compared with the multi-surrogate Expected Hypervolume Improvement. The reasons for the disparities in these methods' effectiveness in maximising the hypervolume of the acquired Pareto Front are investigated. In addition, the effect of the surrogate model mean function on exploration and exploitation is examined: careful choice of data normalisation is shown to be preferable to the exploration parameter commonly used with the Expected Improvement acquisition function. Finally, the effectiveness of all the methodological improvements defined here is demonstrated on a real-world problem: the optimisation of a wind turbine blade aerofoil for both aerodynamic performance and structural stiffness. With effective scalarisation, Bayesian optimisation finds a large number of new aerofoil shapes that strongly dominate standard designs.

Scalarizing Functions in Bayesian Multiobjective Optimization

Scalarizing functions have been widely used to convert a multiobjective optimization problem into a single objective optimization problem. However, their use in solving (computationally) expensive multi- and many-objective optimization problems in Bayesian multiobjective optimization is scarce. Scalarizing functions can play a crucial role on the quality and number of evaluations required when doing the optimization. In this article, we study and review 15 different scalarizing functions in the framework of Bayesian multiobjective optimization and build Gaussian process models (as surrogates, metamodels or emulators) on them. We use expected improvement as infill criterion (or acquisition function) to update the models. In particular, we compare different scalarizing functions and analyze their performance on several benchmark problems with different number of objectives to be optimized. The review and experiments on different functions provide useful insights when using and selecting a scalarizing function when using a Bayesian multiobjective optimization method.