MBORE: Multi-objective Bayesian Optimisation by Density-Ratio Estimation

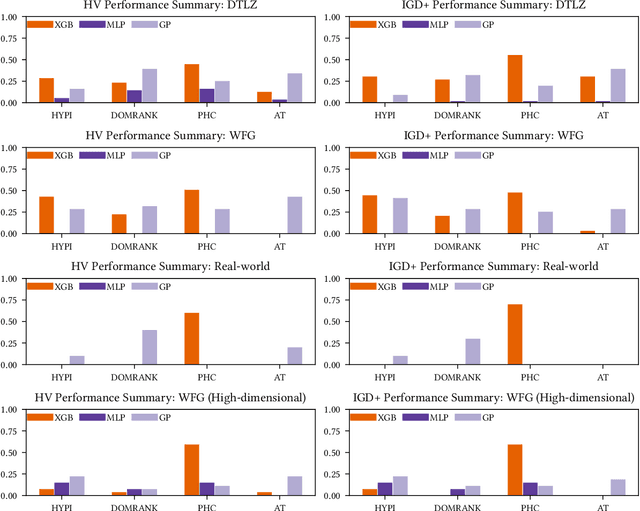
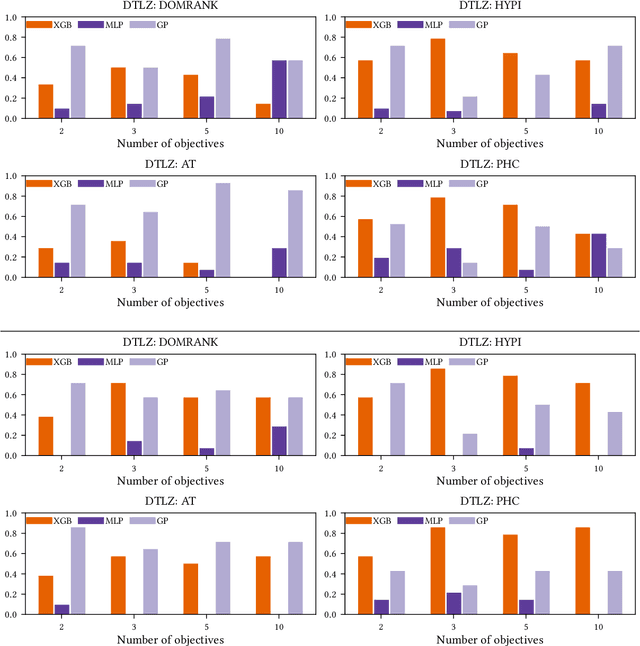
Optimisation problems often have multiple conflicting objectives that can be computationally and/or financially expensive. Mono-surrogate Bayesian optimisation (BO) is a popular model-based approach for optimising such black-box functions. It combines objective values via scalarisation and builds a Gaussian process (GP) surrogate of the scalarised values. The location which maximises a cheap-to-query acquisition function is chosen as the next location to expensively evaluate. While BO is an effective strategy, the use of GPs is limiting. Their performance decreases as the problem input dimensionality increases, and their computational complexity scales cubically with the amount of data. To address these limitations, we extend previous work on BO by density-ratio estimation (BORE) to the multi-objective setting. BORE links the computation of the probability of improvement acquisition function to that of probabilistic classification. This enables the use of state-of-the-art classifiers in a BO-like framework. In this work we present MBORE: multi-objective Bayesian optimisation by density-ratio estimation, and compare it to BO across a range of synthetic and real-world benchmarks. We find that MBORE performs as well as or better than BO on a wide variety of problems, and that it outperforms BO on high-dimensional and real-world problems.

Mixed-Initiative Procedural Content Generation using Level Design Patterns and Interactive Evolutionary Optimisation

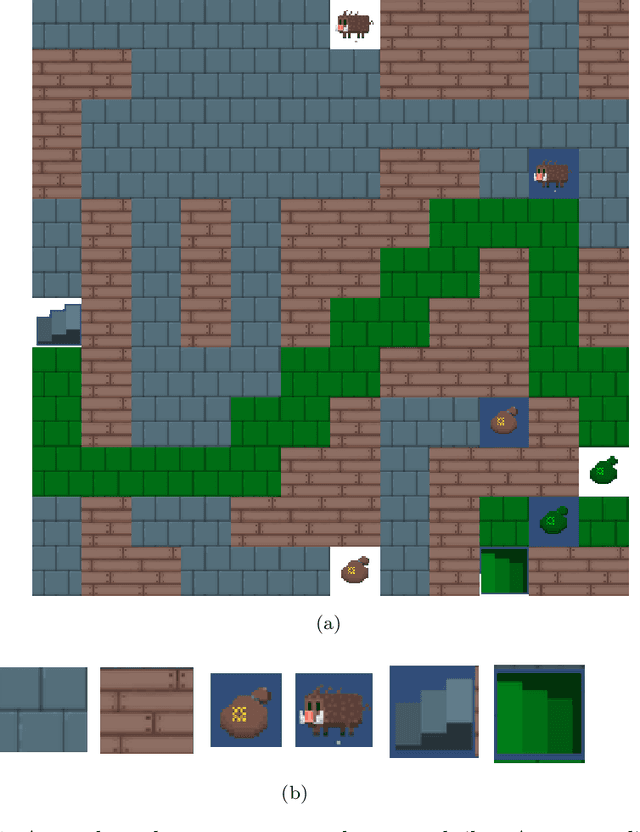
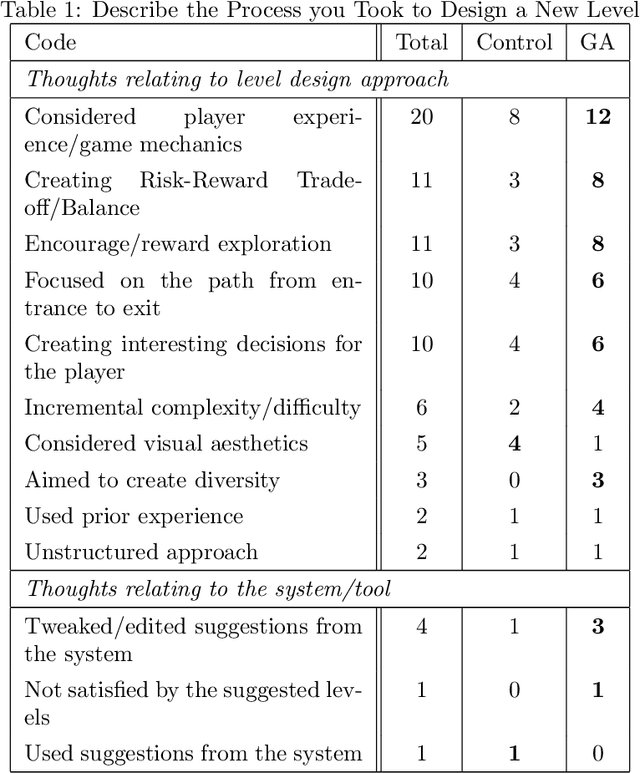
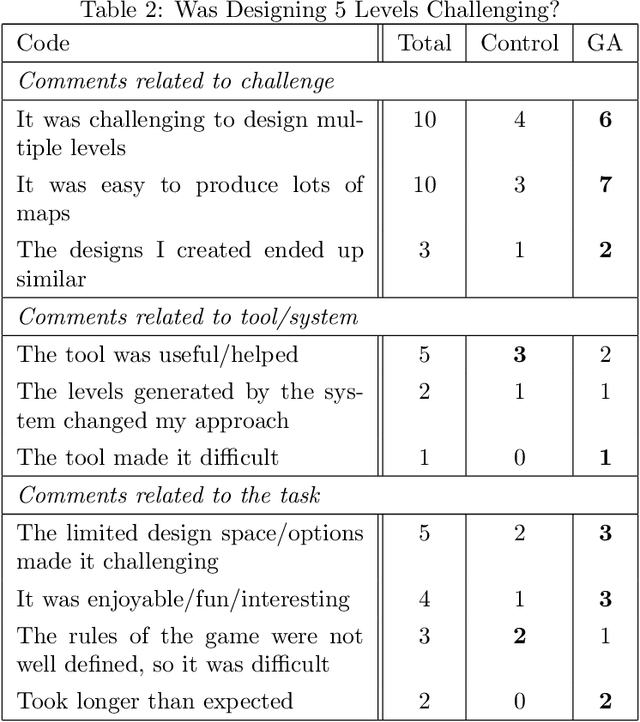
An approach for building mixed-initiative tools for the procedural generation of game levels using interactive evolutionary optimisation is introduced. A tool is created based on this approach which (a) is focused on supporting the designer to explore the design space and (b) only requires the designer to interact with it by designing levels. The tool identifies level design patterns in an initial hand-designed map and uses that information to drive an optimisation algorithm. This results in a number of suggestions which are presented to the designer, who can then edit them providing the system with valuable designer feedback. The effectiveness of this approach to create levels with similar level design patterns to a target is illustrated through a series of algorithm driven benchmark tests. To test the mixed-initiative aspect of the tool a triple-blind mixed-method, user study was conducted. When compared to a control group, provided with random level suggestions throughout the design process, the mixed-initiative approach increased engagement in the level design task and was effective in inspiring new ideas and design directions. This provides significant evidence that procedural content generation can be used as a powerful tool to support the human design process.

$ε$-shotgun: $ε$-greedy Batch Bayesian Optimisation

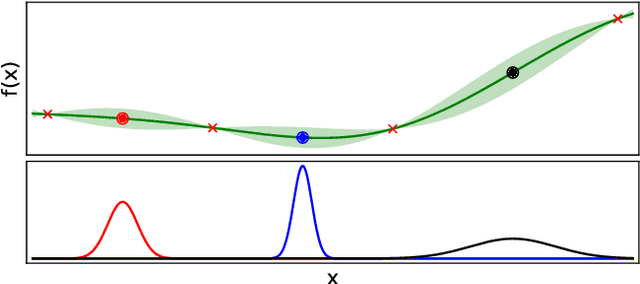
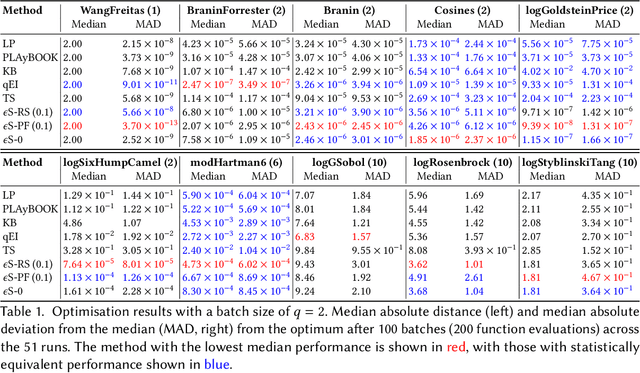
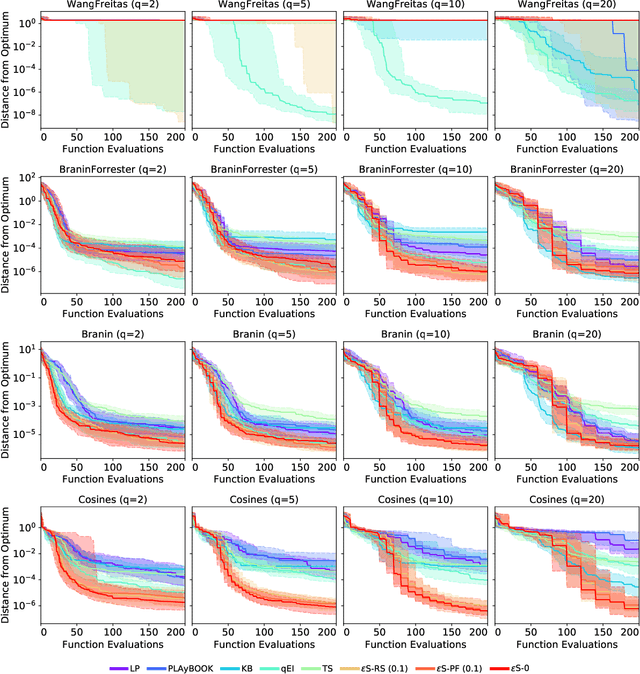
Bayesian optimisation is a popular, surrogate model-based approach for optimising expensive black-box functions. Given a surrogate model, the next location to expensively evaluate is chosen via maximisation of a cheap-to-query acquisition function. We present an $\epsilon$-greedy procedure for Bayesian optimisation in batch settings in which the black-box function can be evaluated multiple times in parallel. Our $\epsilon$-shotgun algorithm leverages the model's prediction, uncertainty, and the approximated rate of change of the landscape to determine the spread of batch solutions to be distributed around a putative location. The initial target location is selected either in an exploitative fashion on the mean prediction, or -- with probability $\epsilon$ -- from elsewhere in the design space. This results in locations that are more densely sampled in regions where the function is changing rapidly and in locations predicted to be good (i.e close to predicted optima), with more scattered samples in regions where the function is flatter and/or of poorer quality. We empirically evaluate the $\epsilon$-shotgun methods on a range of synthetic functions and two real-world problems, finding that they perform at least as well as state-of-the-art batch methods and in many cases exceed their performance.

Greed is Good: Exploration and Exploitation Trade-offs in Bayesian Optimisation

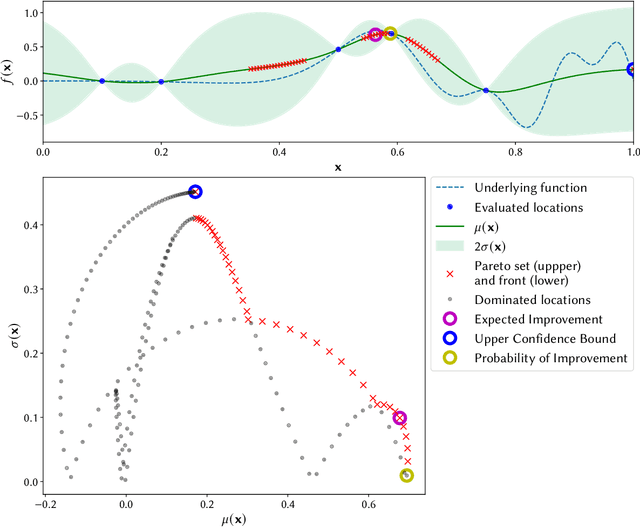
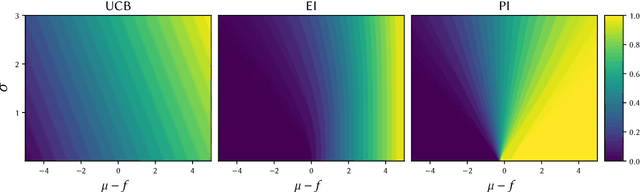
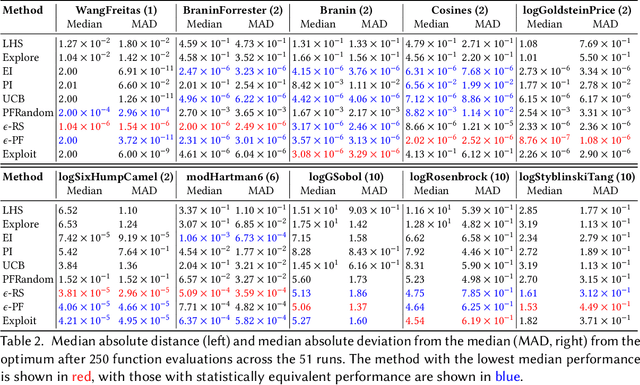
The performance of acquisition functions for Bayesian optimisation is investigated in terms of the Pareto front between exploration and exploitation. We show that Expected Improvement and the Upper Confidence Bound always select solutions to be expensively evaluated on the Pareto front, but Probability of Improvement is never guaranteed to do so and Weighted Expected Improvement does only for a restricted range of weights. We introduce two novel $\epsilon$-greedy acquisition functions. Extensive empirical evaluation of these together with random search, purely exploratory and purely exploitative search on 10 benchmark problems in 1 to 10 dimensions shows that $\epsilon$-greedy algorithms are generally at least as effective as conventional acquisition functions, particularly with a limited budget. In higher dimensions $\epsilon$-greedy approaches are shown to have improved performance over conventional approaches. These results are borne out on a real world computational fluid dynamics optimisation problem and a robotics active learning problem.

A Bayesian Approach for the Robust Optimisation of Expensive-To-Evaluate Functions

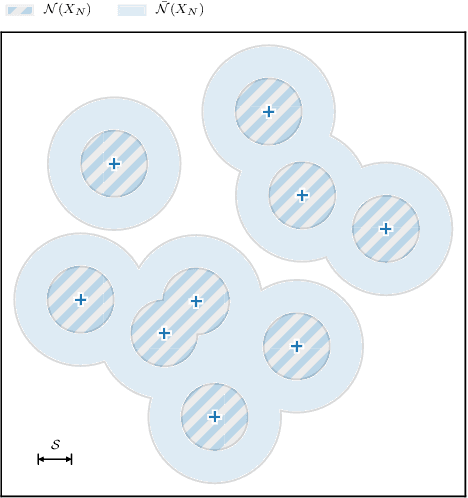
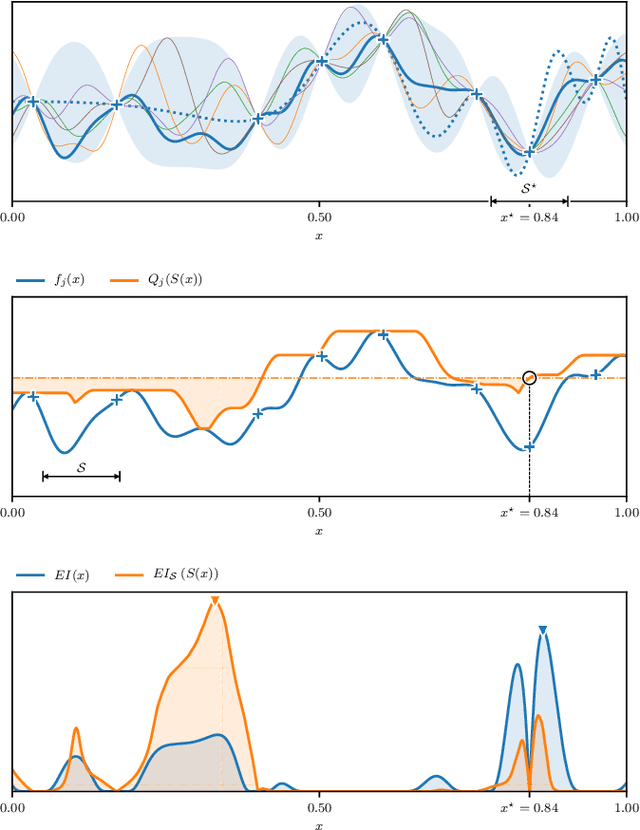
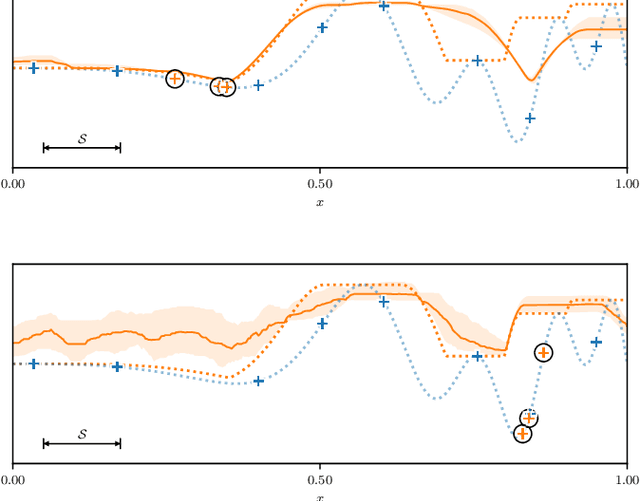
Many expensive black-box optimisation problems are sensitive to their inputs. In these problems it makes more sense to locate a region of good designs, than a single, possible fragile, optimal design. Expensive black-box functions can be optimised effectively with Bayesian optimisation, where a Gaussian process is a popular choice as a prior over the expensive function. We propose a method for robust optimisation using Bayesian optimisation to find a region of design space in which the expensive function's performance is insensitive to the inputs whilst retaining a good quality. This is achieved by sampling realisations from a Gaussian process modelling the expensive function and evaluating the improvement for each realisation. The expectation of these improvements can be optimised cheaply with an evolutionary algorithm to determine the next location at which to evaluate the expensive function. We describe an efficient process to locate the optimum expected improvement. We show empirically that evaluating the expensive function at the location in the candidate sweet spot about which the model is most uncertain or at random yield the best convergence in contrast to exploitative schemes. We illustrate our method on six test functions in two, five, and ten dimensions, and demonstrate that it is able to outperform a state-of-the-art approach from the literature.