A Bayesian Approach for the Robust Optimisation of Expensive-To-Evaluate Functions

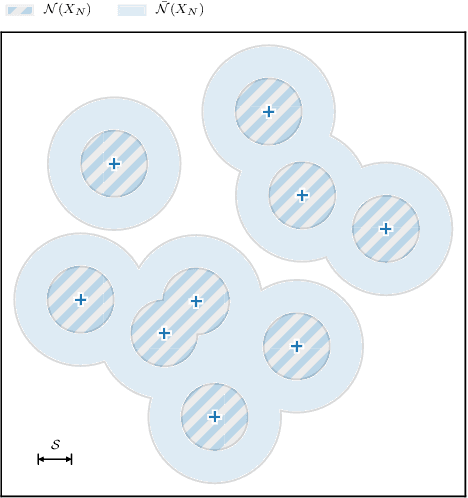
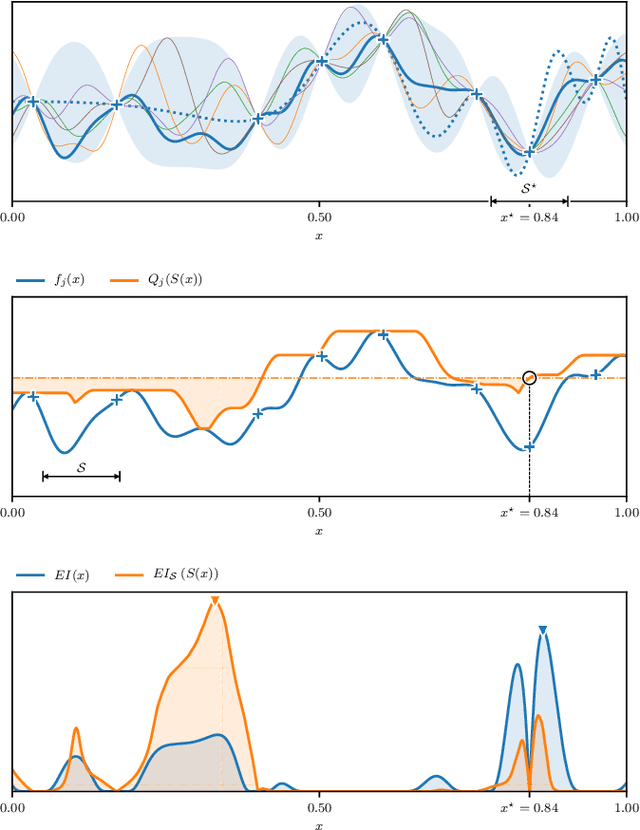
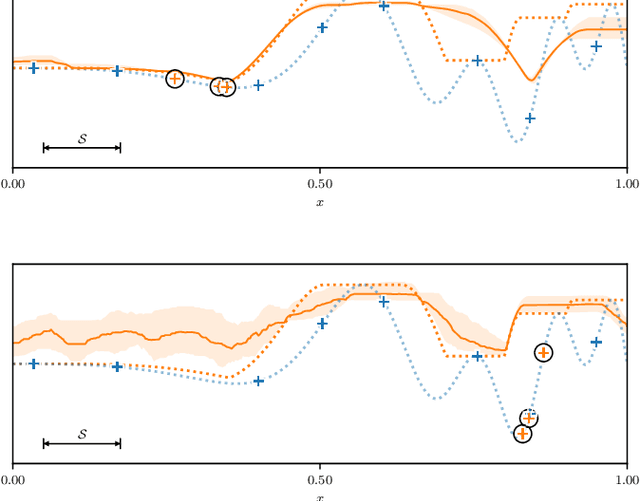
Many expensive black-box optimisation problems are sensitive to their inputs. In these problems it makes more sense to locate a region of good designs, than a single, possible fragile, optimal design. Expensive black-box functions can be optimised effectively with Bayesian optimisation, where a Gaussian process is a popular choice as a prior over the expensive function. We propose a method for robust optimisation using Bayesian optimisation to find a region of design space in which the expensive function's performance is insensitive to the inputs whilst retaining a good quality. This is achieved by sampling realisations from a Gaussian process modelling the expensive function and evaluating the improvement for each realisation. The expectation of these improvements can be optimised cheaply with an evolutionary algorithm to determine the next location at which to evaluate the expensive function. We describe an efficient process to locate the optimum expected improvement. We show empirically that evaluating the expensive function at the location in the candidate sweet spot about which the model is most uncertain or at random yield the best convergence in contrast to exploitative schemes. We illustrate our method on six test functions in two, five, and ten dimensions, and demonstrate that it is able to outperform a state-of-the-art approach from the literature.