Asynchronous ε-Greedy Bayesian Optimisation

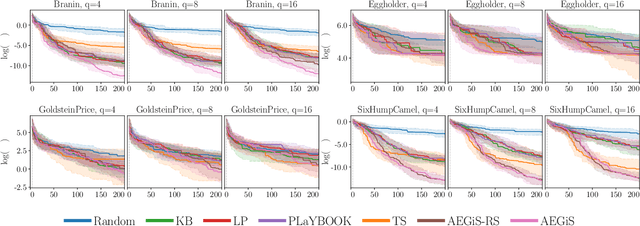
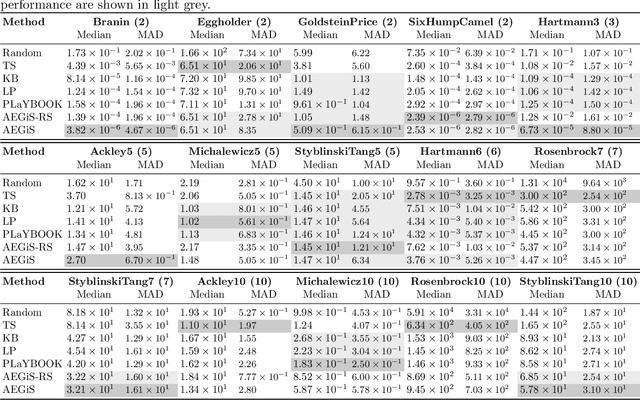
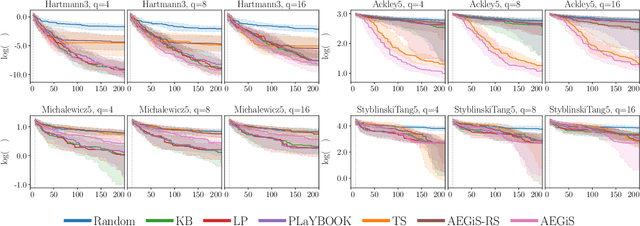
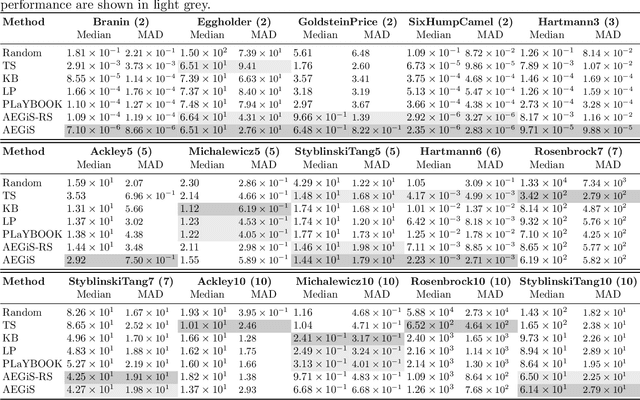
Bayesian Optimisation (BO) is a popular surrogate model-based approach for optimising expensive black-box functions. In order to reduce optimisation wallclock time, parallel evaluation of the black-box function has been proposed. Asynchronous BO allows for a new evaluation to be started as soon as another finishes, thus maximising utilisation of evaluation workers. We present AEGiS (Asynchronous $\epsilon$-Greedy Global Search), an asynchronous BO method that, with probability $2\epsilon$, performs either Thompson sampling or random selection from the approximate Pareto set trading-off between exploitation (surrogate mean prediction) and exploration (surrogate posterior variance). The remaining $1-2\epsilon$ of moves exploit the surrogate's mean prediction. Results on fifteen synthetic benchmark problems, three meta-surrogate hyperparameter tuning problems and two robot pushing problems show that AEGiS generally outperforms existing methods for asynchronous BO. When a single worker is available performance is no worse than BO using expected improvement. We also verify the importance of each of the three components in an ablation study, as well as comparing Pareto set selection to selection from the entire feasible problem domain, finding that the former is vastly superior.

What do you Mean? The Role of the Mean Function in Bayesian Optimisation

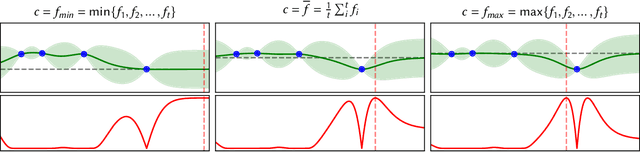
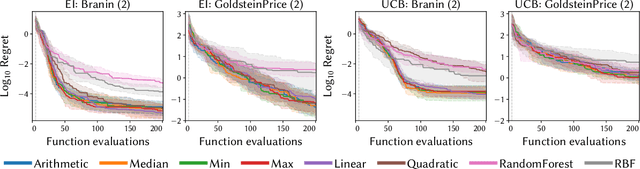
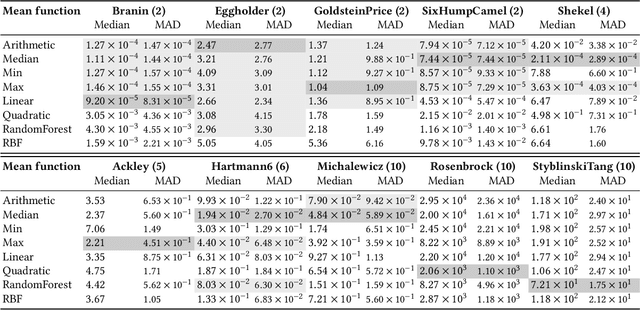
Bayesian optimisation is a popular approach for optimising expensive black-box functions. The next location to be evaluated is selected via maximising an acquisition function that balances exploitation and exploration. Gaussian processes, the surrogate models of choice in Bayesian optimisation, are often used with a constant prior mean function equal to the arithmetic mean of the observed function values. We show that the rate of convergence can depend sensitively on the choice of mean function. We empirically investigate 8 mean functions (constant functions equal to the arithmetic mean, minimum, median and maximum of the observed function evaluations, linear, quadratic polynomials, random forests and RBF networks), using 10 synthetic test problems and two real-world problems, and using the Expected Improvement and Upper Confidence Bound acquisition functions. We find that for design dimensions $\ge5$ using a constant mean function equal to the worst observed quality value is consistently the best choice on the synthetic problems considered. We argue that this worst-observed-quality function promotes exploitation leading to more rapid convergence. However, for the real-world tasks the more complex mean functions capable of modelling the fitness landscape may be effective, although there is no clearly optimum choice.

$ε$-shotgun: $ε$-greedy Batch Bayesian Optimisation

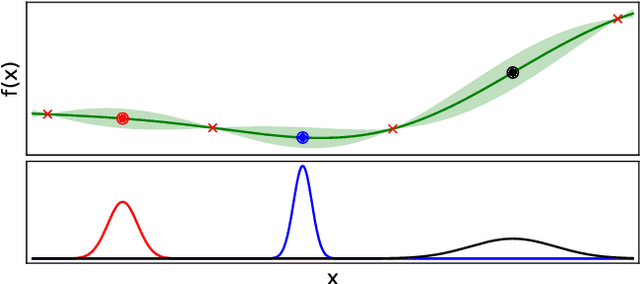
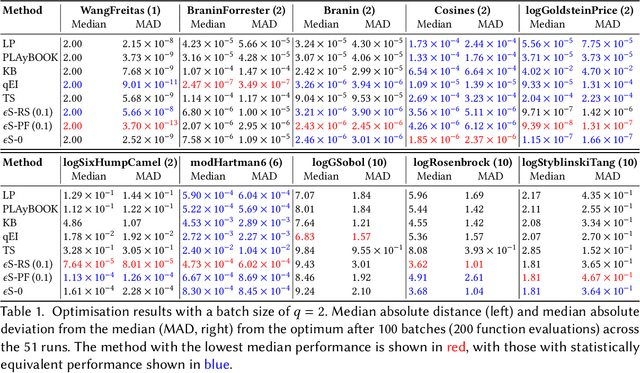
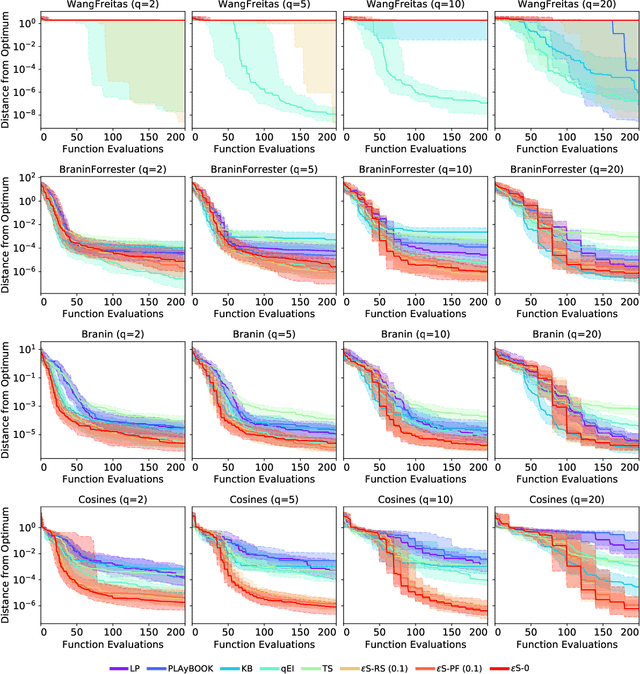
Bayesian optimisation is a popular, surrogate model-based approach for optimising expensive black-box functions. Given a surrogate model, the next location to expensively evaluate is chosen via maximisation of a cheap-to-query acquisition function. We present an $\epsilon$-greedy procedure for Bayesian optimisation in batch settings in which the black-box function can be evaluated multiple times in parallel. Our $\epsilon$-shotgun algorithm leverages the model's prediction, uncertainty, and the approximated rate of change of the landscape to determine the spread of batch solutions to be distributed around a putative location. The initial target location is selected either in an exploitative fashion on the mean prediction, or -- with probability $\epsilon$ -- from elsewhere in the design space. This results in locations that are more densely sampled in regions where the function is changing rapidly and in locations predicted to be good (i.e close to predicted optima), with more scattered samples in regions where the function is flatter and/or of poorer quality. We empirically evaluate the $\epsilon$-shotgun methods on a range of synthetic functions and two real-world problems, finding that they perform at least as well as state-of-the-art batch methods and in many cases exceed their performance.

Greed is Good: Exploration and Exploitation Trade-offs in Bayesian Optimisation

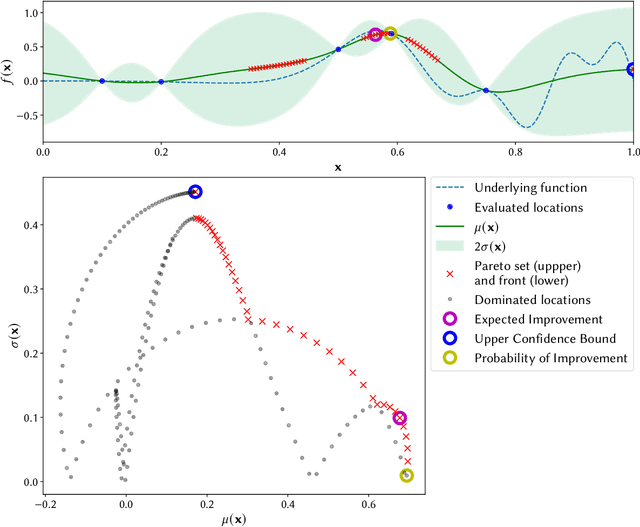
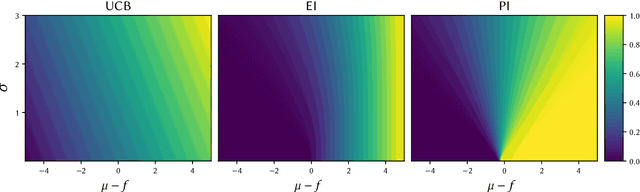
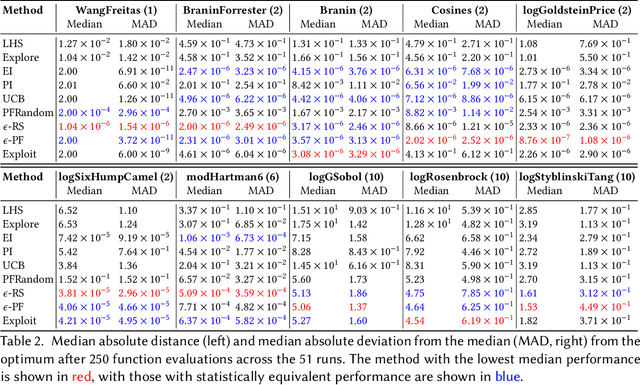
The performance of acquisition functions for Bayesian optimisation is investigated in terms of the Pareto front between exploration and exploitation. We show that Expected Improvement and the Upper Confidence Bound always select solutions to be expensively evaluated on the Pareto front, but Probability of Improvement is never guaranteed to do so and Weighted Expected Improvement does only for a restricted range of weights. We introduce two novel $\epsilon$-greedy acquisition functions. Extensive empirical evaluation of these together with random search, purely exploratory and purely exploitative search on 10 benchmark problems in 1 to 10 dimensions shows that $\epsilon$-greedy algorithms are generally at least as effective as conventional acquisition functions, particularly with a limited budget. In higher dimensions $\epsilon$-greedy approaches are shown to have improved performance over conventional approaches. These results are borne out on a real world computational fluid dynamics optimisation problem and a robotics active learning problem.

A Bayesian Approach for the Robust Optimisation of Expensive-To-Evaluate Functions

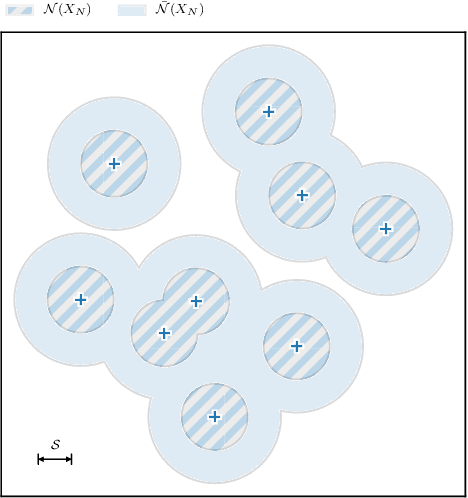
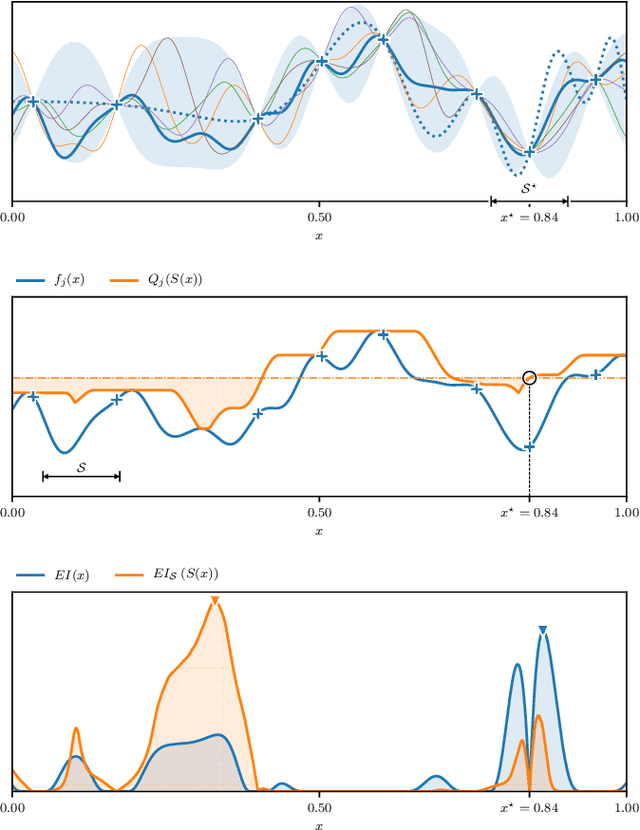
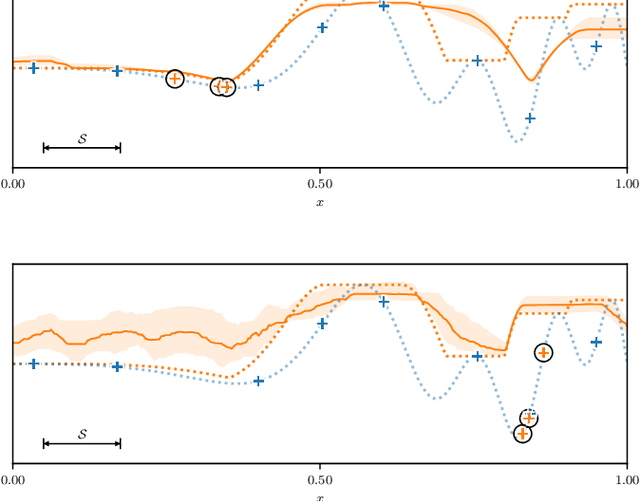
Many expensive black-box optimisation problems are sensitive to their inputs. In these problems it makes more sense to locate a region of good designs, than a single, possible fragile, optimal design. Expensive black-box functions can be optimised effectively with Bayesian optimisation, where a Gaussian process is a popular choice as a prior over the expensive function. We propose a method for robust optimisation using Bayesian optimisation to find a region of design space in which the expensive function's performance is insensitive to the inputs whilst retaining a good quality. This is achieved by sampling realisations from a Gaussian process modelling the expensive function and evaluating the improvement for each realisation. The expectation of these improvements can be optimised cheaply with an evolutionary algorithm to determine the next location at which to evaluate the expensive function. We describe an efficient process to locate the optimum expected improvement. We show empirically that evaluating the expensive function at the location in the candidate sweet spot about which the model is most uncertain or at random yield the best convergence in contrast to exploitative schemes. We illustrate our method on six test functions in two, five, and ten dimensions, and demonstrate that it is able to outperform a state-of-the-art approach from the literature.

Comparison of the Bayesian and Randomised Decision Tree Ensembles within an Uncertainty Envelope Technique

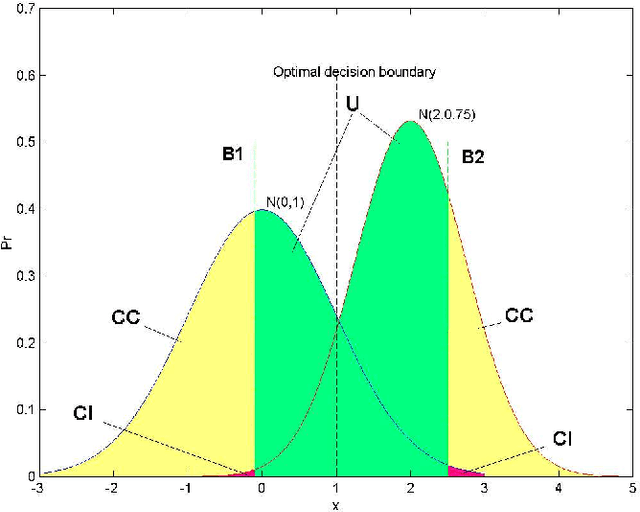
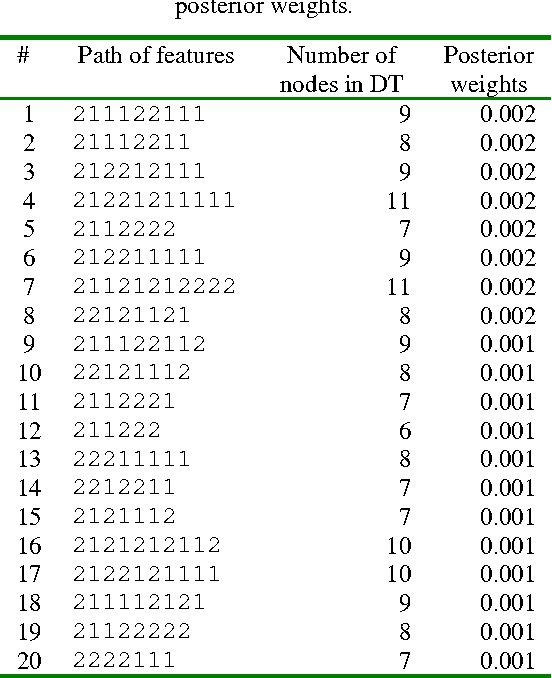
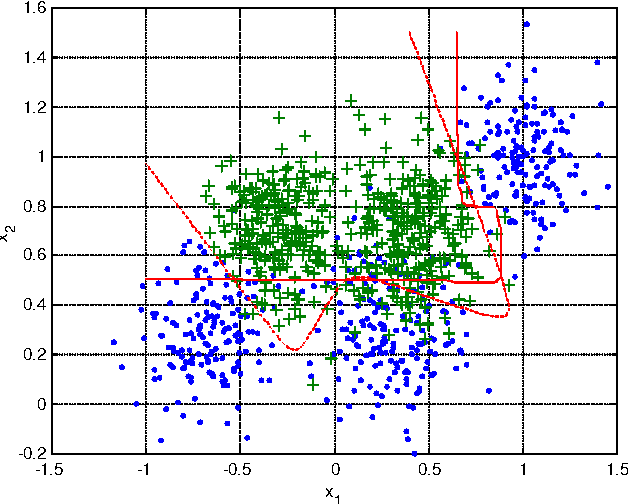
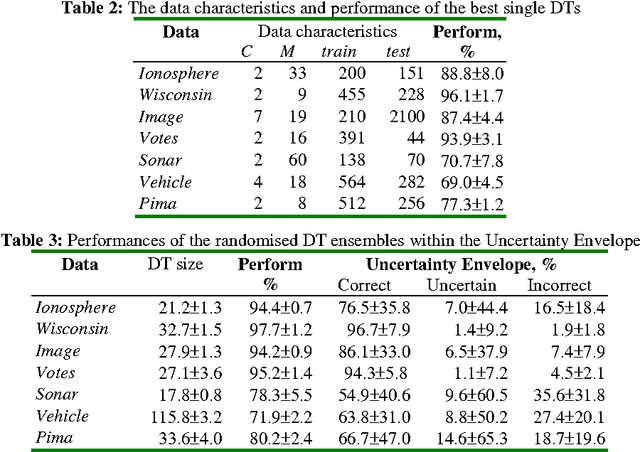
Multiple Classifier Systems (MCSs) allow evaluation of the uncertainty of classification outcomes that is of crucial importance for safety critical applications. The uncertainty of classification is determined by a trade-off between the amount of data available for training, the classifier diversity and the required performance. The interpretability of MCSs can also give useful information for experts responsible for making reliable classifications. For this reason Decision Trees (DTs) seem to be attractive classification models for experts. The required diversity of MCSs exploiting such classification models can be achieved by using two techniques, the Bayesian model averaging and the randomised DT ensemble. Both techniques have revealed promising results when applied to real-world problems. In this paper we experimentally compare the classification uncertainty of the Bayesian model averaging with a restarting strategy and the randomised DT ensemble on a synthetic dataset and some domain problems commonly used in the machine learning community. To make the Bayesian DT averaging feasible, we use a Markov Chain Monte Carlo technique. The classification uncertainty is evaluated within an Uncertainty Envelope technique dealing with the class posterior distribution and a given confidence probability. Exploring a full posterior distribution, this technique produces realistic estimates which can be easily interpreted in statistical terms. In our experiments we found out that the Bayesian DTs are superior to the randomised DT ensembles within the Uncertainty Envelope technique.

Estimating Classification Uncertainty of Bayesian Decision Tree Technique on Financial Data

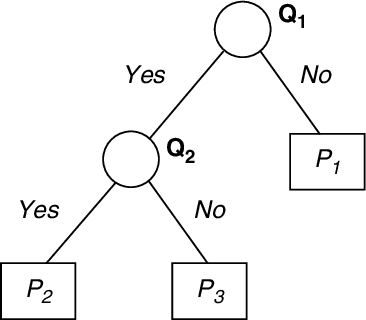
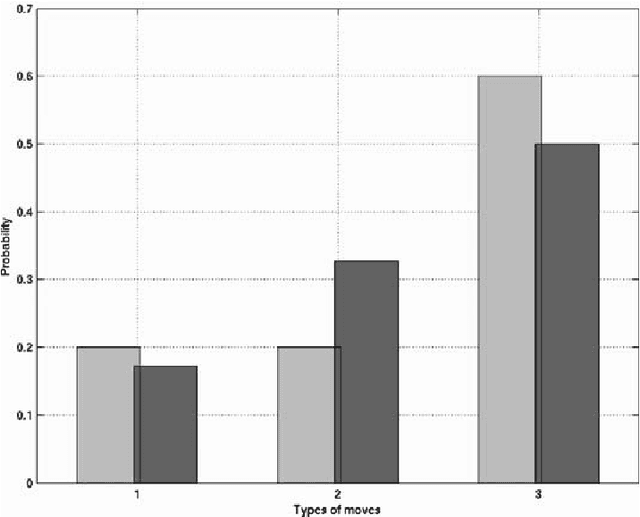
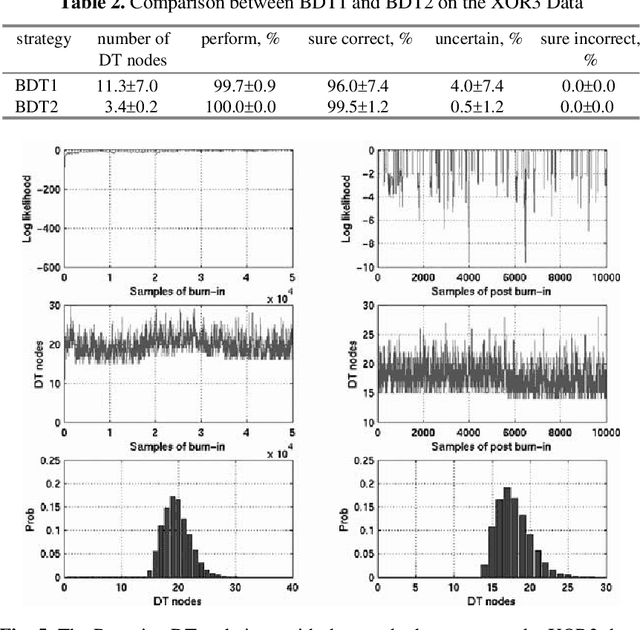
Bayesian averaging over classification models allows the uncertainty of classification outcomes to be evaluated, which is of crucial importance for making reliable decisions in applications such as financial in which risks have to be estimated. The uncertainty of classification is determined by a trade-off between the amount of data available for training, the diversity of a classifier ensemble and the required performance. The interpretability of classification models can also give useful information for experts responsible for making reliable classifications. For this reason Decision Trees (DTs) seem to be attractive classification models. The required diversity of the DT ensemble can be achieved by using the Bayesian model averaging all possible DTs. In practice, the Bayesian approach can be implemented on the base of a Markov Chain Monte Carlo (MCMC) technique of random sampling from the posterior distribution. For sampling large DTs, the MCMC method is extended by Reversible Jump technique which allows inducing DTs under given priors. For the case when the prior information on the DT size is unavailable, the sweeping technique defining the prior implicitly reveals a better performance. Within this Chapter we explore the classification uncertainty of the Bayesian MCMC techniques on some datasets from the StatLog Repository and real financial data. The classification uncertainty is compared within an Uncertainty Envelope technique dealing with the class posterior distribution and a given confidence probability. This technique provides realistic estimates of the classification uncertainty which can be easily interpreted in statistical terms with the aim of risk evaluation.