Estimating Classification Uncertainty of Bayesian Decision Tree Technique on Financial Data
Paper and Code
Apr 14, 2005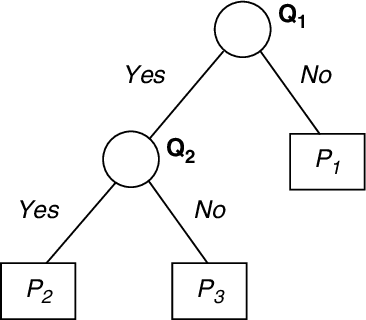

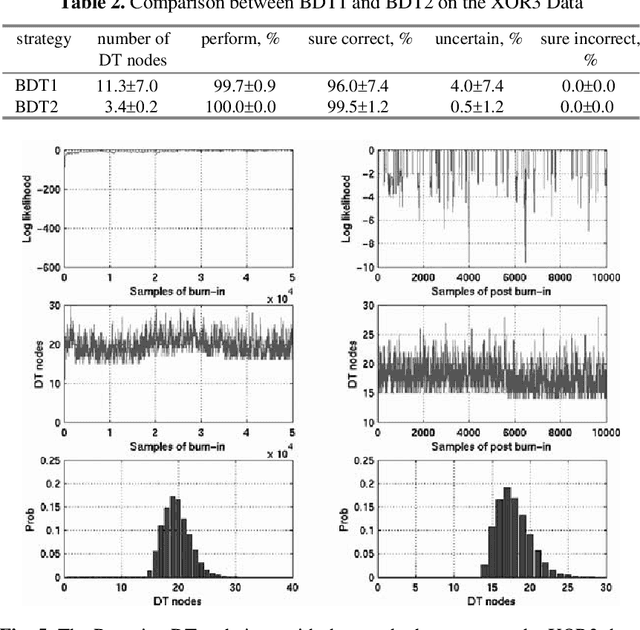
Bayesian averaging over classification models allows the uncertainty of classification outcomes to be evaluated, which is of crucial importance for making reliable decisions in applications such as financial in which risks have to be estimated. The uncertainty of classification is determined by a trade-off between the amount of data available for training, the diversity of a classifier ensemble and the required performance. The interpretability of classification models can also give useful information for experts responsible for making reliable classifications. For this reason Decision Trees (DTs) seem to be attractive classification models. The required diversity of the DT ensemble can be achieved by using the Bayesian model averaging all possible DTs. In practice, the Bayesian approach can be implemented on the base of a Markov Chain Monte Carlo (MCMC) technique of random sampling from the posterior distribution. For sampling large DTs, the MCMC method is extended by Reversible Jump technique which allows inducing DTs under given priors. For the case when the prior information on the DT size is unavailable, the sweeping technique defining the prior implicitly reveals a better performance. Within this Chapter we explore the classification uncertainty of the Bayesian MCMC techniques on some datasets from the StatLog Repository and real financial data. The classification uncertainty is compared within an Uncertainty Envelope technique dealing with the class posterior distribution and a given confidence probability. This technique provides realistic estimates of the classification uncertainty which can be easily interpreted in statistical terms with the aim of risk evaluation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge