A Bayesian Active Learning Approach to Comparative Judgement

Assessment is a crucial part of education. Traditional marking is a source of inconsistencies and unconscious bias, placing a high cognitive load on the assessors. An approach to address these issues is comparative judgement (CJ). In CJ, the assessor is presented with a pair of items and is asked to select the better one. Following a series of comparisons, a rank is derived using a ranking model, for example, the BTM, based on the results. While CJ is considered a reliable method for marking, there are concerns around transparency, and the ideal number of pairwise comparisons to generate a reliable estimation of the rank order is not known. Additionally, there have been attempts to generate a method of selecting pairs that should be compared next in an informative manner, but some existing methods are known to have created their own bias within results inflating the reliability metric used. As a result, a random selection approach is usually deployed. We propose a novel Bayesian approach to CJ (BCJ) for determining the ranks of compared items alongside a new way to select the pairs to present to the marker(s) using active learning (AL), addressing the key shortcomings of traditional CJ. Furthermore, we demonstrate how the entire approach may provide transparency by providing the user insights into how it is making its decisions and, at the same time, being more efficient. Results from our experiments confirm that the proposed BCJ combined with entropy-driven AL pair-selection method is superior to other alternatives. We also find that the more comparisons done, the more accurate BCJ becomes, which solves the issue the current method has of the model deteriorating if too many comparisons are performed. As our approach can generate the complete predicted rank distribution for an item, we also show how this can be utilised in devising a predicted grade, guided by the assessor.

Efficient Approximation of Expected Hypervolume Improvement using Gauss-Hermite Quadrature

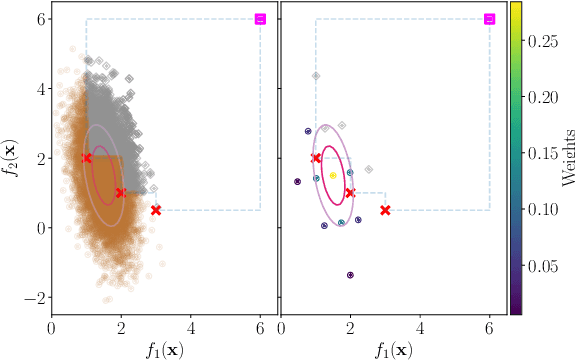
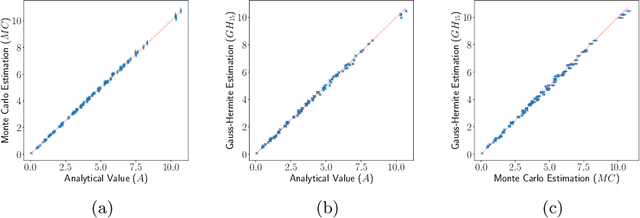
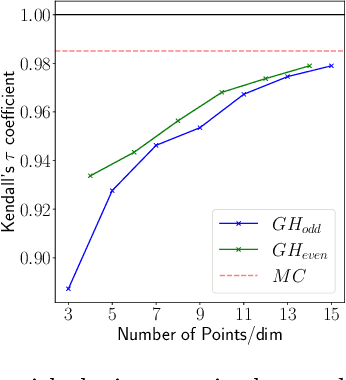
Many methods for performing multi-objective optimisation of computationally expensive problems have been proposed recently. Typically, a probabilistic surrogate for each objective is constructed from an initial dataset. The surrogates can then be used to produce predictive densities in the objective space for any solution. Using the predictive densities, we can compute the expected hypervolume improvement (EHVI) due to a solution. Maximising the EHVI, we can locate the most promising solution that may be expensively evaluated next. There are closed-form expressions for computing the EHVI, integrating over the multivariate predictive densities. However, they require partitioning the objective space, which can be prohibitively expensive for more than three objectives. Furthermore, there are no closed-form expressions for a problem where the predictive densities are dependent, capturing the correlations between objectives. Monte Carlo approximation is used instead in such cases, which is not cheap. Hence, the need to develop new accurate but cheaper approximation methods remains. Here we investigate an alternative approach toward approximating the EHVI using Gauss-Hermite quadrature. We show that it can be an accurate alternative to Monte Carlo for both independent and correlated predictive densities with statistically significant rank correlations for a range of popular test problems.

What Makes an Effective Scalarising Function for Multi-Objective Bayesian Optimisation?

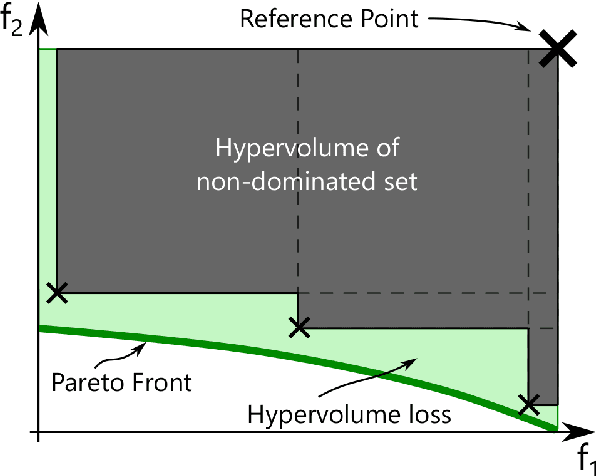
Performing multi-objective Bayesian optimisation by scalarising the objectives avoids the computation of expensive multi-dimensional integral-based acquisition functions, instead of allowing one-dimensional standard acquisition functions\textemdash such as Expected Improvement\textemdash to be applied. Here, two infill criteria based on hypervolume improvement\textemdash one recently introduced and one novel\textemdash are compared with the multi-surrogate Expected Hypervolume Improvement. The reasons for the disparities in these methods' effectiveness in maximising the hypervolume of the acquired Pareto Front are investigated. In addition, the effect of the surrogate model mean function on exploration and exploitation is examined: careful choice of data normalisation is shown to be preferable to the exploration parameter commonly used with the Expected Improvement acquisition function. Finally, the effectiveness of all the methodological improvements defined here is demonstrated on a real-world problem: the optimisation of a wind turbine blade aerofoil for both aerodynamic performance and structural stiffness. With effective scalarisation, Bayesian optimisation finds a large number of new aerofoil shapes that strongly dominate standard designs.

On Bayesian Search for the Feasible Space Under Computationally Expensive Constraints

We are often interested in identifying the feasible subset of a decision space under multiple constraints. However, in cases where the constraints cannot be represented by analytical formulae, the cost of solving these problems can be prohibitive, since the only way to determine feasibility is to run computationally or financially expensive simulations. We propose a novel approach for this problem: we learn a surrogate classifier that can rapidly and accurately identify feasible solutions using only a very limited number of samples ($11n$, where $n$ is the dimension of the decision space) obviating the need for full simulations. This is a data-efficient active-learning approach using Gaussian processes (GPs), a form of Bayesian regression models, and we refer to this method as Bayesian search. Using a small training set to begin with, we train a GP model for each constraint. The algorithm then identifies the next decision vector to expensively evaluate using an acquisition function. We subsequently augment the training data set with each newly evaluated solution, improving the accuracy of the estimated feasibility on each step. This iterative process continues until the limit on the number of expensive evaluations is reached. Initially, we adapted acquisition functions from the reliability engineering literature for this purpose. However, these acquisition functions do not appropriately consider the uncertainty in predictions offered by the GP models. We, therefore, introduce a new acquisition function to account for this. The new acquisition function combines the probability that a solution lies at the boundary between feasible and infeasible spaces representing exploitation) as well as the entropy in predictions (representing exploration). In our experiments, the best classifier has a median informedness of at least $97.95\%$ across five of the G problems.