What Makes an Effective Scalarising Function for Multi-Objective Bayesian Optimisation?
Paper and Code
Apr 10, 2021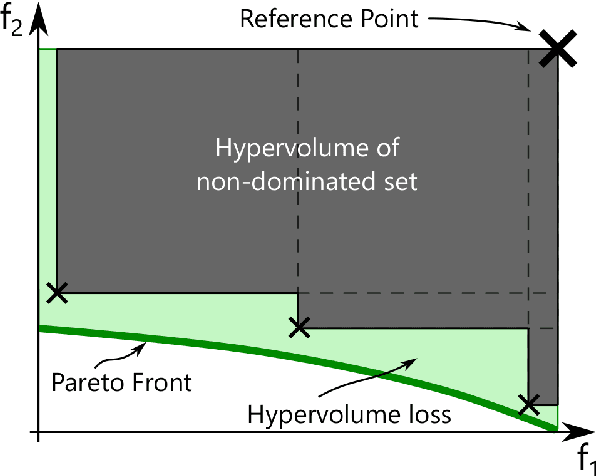


Performing multi-objective Bayesian optimisation by scalarising the objectives avoids the computation of expensive multi-dimensional integral-based acquisition functions, instead of allowing one-dimensional standard acquisition functions\textemdash such as Expected Improvement\textemdash to be applied. Here, two infill criteria based on hypervolume improvement\textemdash one recently introduced and one novel\textemdash are compared with the multi-surrogate Expected Hypervolume Improvement. The reasons for the disparities in these methods' effectiveness in maximising the hypervolume of the acquired Pareto Front are investigated. In addition, the effect of the surrogate model mean function on exploration and exploitation is examined: careful choice of data normalisation is shown to be preferable to the exploration parameter commonly used with the Expected Improvement acquisition function. Finally, the effectiveness of all the methodological improvements defined here is demonstrated on a real-world problem: the optimisation of a wind turbine blade aerofoil for both aerodynamic performance and structural stiffness. With effective scalarisation, Bayesian optimisation finds a large number of new aerofoil shapes that strongly dominate standard designs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge