Regret Analysis of Policy Optimization over Submanifolds for Linearly Constrained Online LQG

Recent advancement in online optimization and control has provided novel tools to study online linear quadratic regulator (LQR) problems, where cost matrices are varying adversarially over time. However, the controller parameterization of existing works may not satisfy practical conditions like sparsity due to physical connections. In this work, we study online linear quadratic Gaussian problems with a given linear constraint imposed on the controller. Inspired by the recent work of [1] which proposed, for a linearly constrained policy optimization of an offline LQR, a second order method equipped with a Riemannian metric that emerges naturally in the context of optimal control problems, we propose online optimistic Newton on manifold (OONM) which provides an online controller based on the prediction on the first and second order information of the function sequence. To quantify the proposed algorithm, we leverage the notion of regret defined as the sub-optimality of its cumulative cost to that of a (locally) minimizing controller sequence and provide the regret bound in terms of the path-length of the minimizer sequence. Simulation results are also provided to verify the property of OONM.

Regret Analysis of Distributed Online Control for LTI Systems with Adversarial Disturbances

This paper addresses the distributed online control problem over a network of linear time-invariant (LTI) systems (with possibly unknown dynamics) in the presence of adversarial perturbations. There exists a global network cost that is characterized by a time-varying convex function, which evolves in an adversarial manner and is sequentially and partially observed by local agents. The goal of each agent is to generate a control sequence that can compete with the best centralized control policy in hindsight, which has access to the global cost. This problem is formulated as a regret minimization. For the case of known dynamics, we propose a fully distributed disturbance feedback controller that guarantees a regret bound of $O(\sqrt{T}\log T)$, where $T$ is the time horizon. For the unknown dynamics case, we design a distributed explore-then-commit approach, where in the exploration phase all agents jointly learn the system dynamics, and in the learning phase our proposed control algorithm is applied using each agent system estimate. We establish a regret bound of $O(T^{2/3} \text{poly}(\log T))$ for this setting.

Dynamic Regret Analysis of Safe Distributed Online Optimization for Convex and Non-convex Problems

This paper addresses safe distributed online optimization over an unknown set of linear safety constraints. A network of agents aims at jointly minimizing a global, time-varying function, which is only partially observable to each individual agent. Therefore, agents must engage in local communications to generate a safe sequence of actions competitive with the best minimizer sequence in hindsight, and the gap between the two sequences is quantified via dynamic regret. We propose distributed safe online gradient descent (D-Safe-OGD) with an exploration phase, where all agents estimate the constraint parameters collaboratively to build estimated feasible sets, ensuring the action selection safety during the optimization phase. We prove that for convex functions, D-Safe-OGD achieves a dynamic regret bound of $O(T^{2/3} \sqrt{\log T} + T^{1/3}C_T^*)$, where $C_T^*$ denotes the path-length of the best minimizer sequence. We further prove a dynamic regret bound of $O(T^{2/3} \sqrt{\log T} + T^{2/3}C_T^*)$ for certain non-convex problems, which establishes the first dynamic regret bound for a safe distributed algorithm in the non-convex setting.

Distributed Online System Identification for LTI Systems Using Reverse Experience Replay

Identification of linear time-invariant (LTI) systems plays an important role in control and reinforcement learning. Both asymptotic and finite-time offline system identification are well-studied in the literature. For online system identification, the idea of stochastic-gradient descent with reverse experience replay (SGD-RER) was recently proposed, where the data sequence is stored in several buffers and the stochastic-gradient descent (SGD) update performs backward in each buffer to break the time dependency between data points. Inspired by this work, we study distributed online system identification of LTI systems over a multi-agent network. We consider agents as identical LTI systems, and the network goal is to jointly estimate the system parameters by leveraging the communication between agents. We propose DSGD-RER, a distributed variant of the SGD-RER algorithm, and theoretically characterize the improvement of the estimation error with respect to the network size. Our numerical experiments certify the reduction of estimation error as the network size grows.

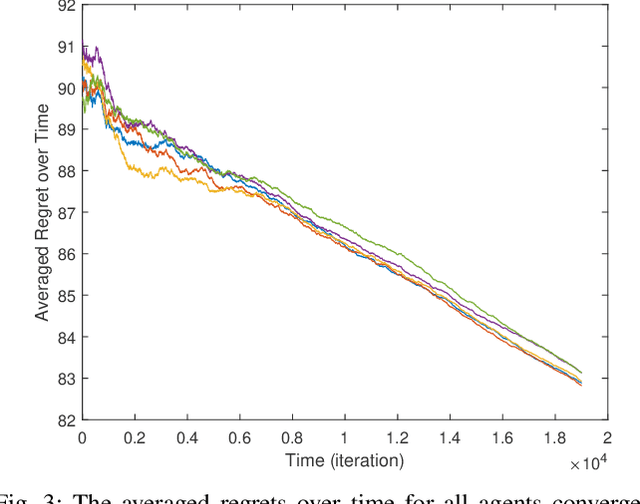
Regret Analysis of Distributed Online LQR Control for Unknown LTI Systems

Online learning has recently opened avenues for rethinking classical optimal control beyond time-invariant cost metrics, and online controllers are designed when the performance criteria changes adversarially over time. Inspired by this line of research, we study the distributed online linear quadratic regulator (LQR) problem for linear time-invariant (LTI) systems with unknown dynamics. Consider a multi-agent network where each agent is modeled as a LTI system. The LTI systems are associated with time-varying quadratic costs that are revealed sequentially. The goal of the network is to collectively (i) estimate the unknown dynamics and (ii) compute local control sequences competitive to that of the best centralized policy in hindsight that minimizes the sum of costs for all agents. This problem is formulated as a {\it regret} minimization. We propose a distributed variant of the online LQR algorithm where each agent computes its system estimate during an exploration stage. The agent then applies distributed online gradient descent on a semi-definite programming (SDP) whose feasible set is based on the agent's system estimate. We prove that the regret bound of our proposed algorithm scales $\tilde{O}(T^{2/3})$, implying the consensus of the network over time. We also provide simulation results verifying our theoretical guarantee.

Distributed Online Linear Quadratic Control for Linear Time-invariant Systems

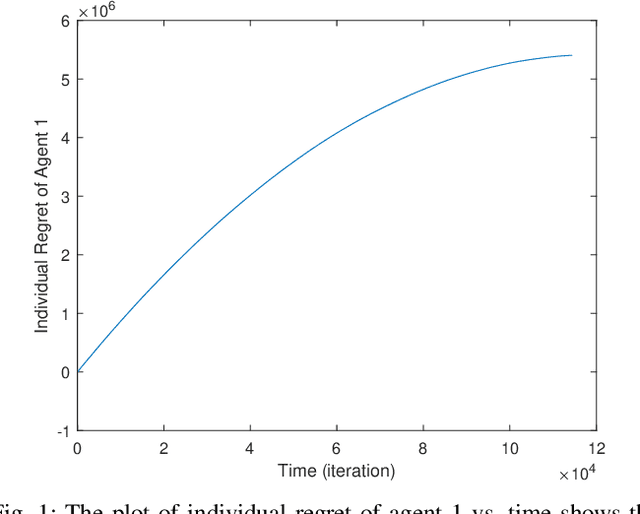
Classical linear quadratic (LQ) control centers around linear time-invariant (LTI) systems, where the control-state pairs introduce a quadratic cost with time-invariant parameters. Recent advancement in online optimization and control has provided novel tools to study LQ problems that are robust to time-varying cost parameters. Inspired by this line of research, we study the distributed online LQ problem for identical LTI systems. Consider a multi-agent network where each agent is modeled as an LTI system. The LTI systems are associated with decoupled, time-varying quadratic costs that are revealed sequentially. The goal of the network is to make the control sequence of all agents competitive to that of the best centralized policy in hindsight, captured by the notion of regret. We develop a distributed variant of the online LQ algorithm, which runs distributed online gradient descent with a projection to a semi-definite programming (SDP) to generate controllers. We establish a regret bound scaling as the square root of the finite time-horizon, implying that agents reach consensus as time grows. We further provide numerical experiments verifying our theoretical result.

Unconstrained Online Optimization: Dynamic Regret Analysis of Strongly Convex and Smooth Problems

The regret bound of dynamic online learning algorithms is often expressed in terms of the variation in the function sequence ($V_T$) and/or the path-length of the minimizer sequence after $T$ rounds. For strongly convex and smooth functions, , Zhang et al. establish the squared path-length of the minimizer sequence ($C^*_{2,T}$) as a lower bound on regret. They also show that online gradient descent (OGD) achieves this lower bound using multiple gradient queries per round. In this paper, we focus on unconstrained online optimization. We first show that a preconditioned variant of OGD achieves $O(C^*_{2,T})$ with one gradient query per round. We then propose online optimistic Newton (OON) method for the case when the first and second order information of the function sequence is predictable. The regret bound of OON is captured via the quartic path-length of the minimizer sequence ($C^*_{4,T}$), which can be much smaller than $C^*_{2,T}$. We finally show that by using multiple gradients for OGD, we can achieve an upper bound of $O(\min\{C^*_{2,T},V_T\})$ on regret.

A Random-Feature Based Newton Method for Empirical Risk Minimization in Reproducing Kernel Hilbert Space

In supervised learning using kernel methods, we encounter a large-scale finite-sum minimization over a reproducing kernel Hilbert space(RKHS). Often times large-scale finite-sum problems can be solved using efficient variants of Newton's method where the Hessian is approximated via sub-samples. In RKHS, however, the dependence of the penalty function to kernel makes standard sub-sampling approaches inapplicable, since the gram matrix is not readily available in a low-rank form. In this paper, we observe that for this class of problems, one can naturally use kernel approximation to speed up the Newton's method. Focusing on randomized features for kernel approximation, we provide a novel second-order algorithm that enjoys local superlinear convergence and global convergence in the high probability sense. The key to our analysis is showing that the approximated Hessian via random features preserves the spectrum of the original Hessian. We provide numerical experiments verifying the efficiency of our approach, compared to variants of sub-sampling methods.

Efficient Two-Step Adversarial Defense for Deep Neural Networks

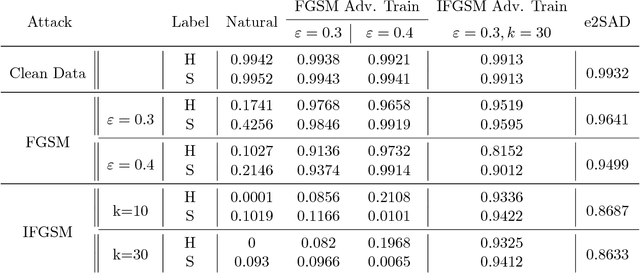
In recent years, deep neural networks have demonstrated outstanding performance in many machine learning tasks. However, researchers have discovered that these state-of-the-art models are vulnerable to adversarial examples: legitimate examples added by small perturbations which are unnoticeable to human eyes. Adversarial training, which augments the training data with adversarial examples during the training process, is a well known defense to improve the robustness of the model against adversarial attacks. However, this robustness is only effective to the same attack method used for adversarial training. Madry et al.(2017) suggest that effectiveness of iterative multi-step adversarial attacks and particularly that projected gradient descent (PGD) may be considered the universal first order adversary and applying the adversarial training with PGD implies resistance against many other first order attacks. However, the computational cost of the adversarial training with PGD and other multi-step adversarial examples is much higher than that of the adversarial training with other simpler attack techniques. In this paper, we show how strong adversarial examples can be generated only at a cost similar to that of two runs of the fast gradient sign method (FGSM), allowing defense against adversarial attacks with a robustness level comparable to that of the adversarial training with multi-step adversarial examples. We empirically demonstrate the effectiveness of the proposed two-step defense approach against different attack methods and its improvements over existing defense strategies.