Timoteo Carletti
Bio-inspired decision making in swarms under biases from stubborn robots, corrupted communication, and independent discovery
Sep 09, 2025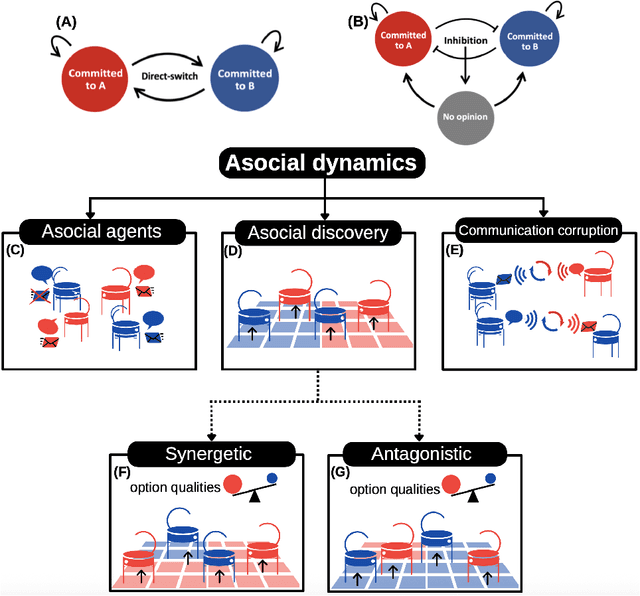
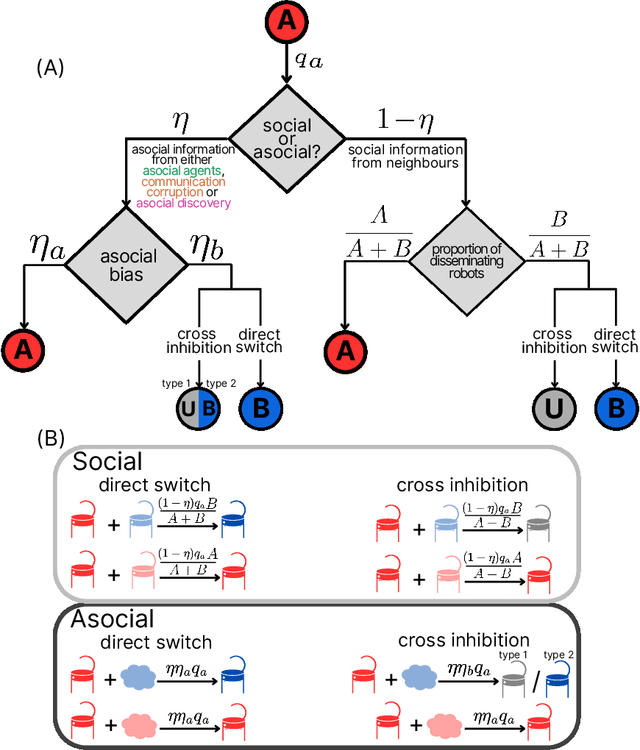
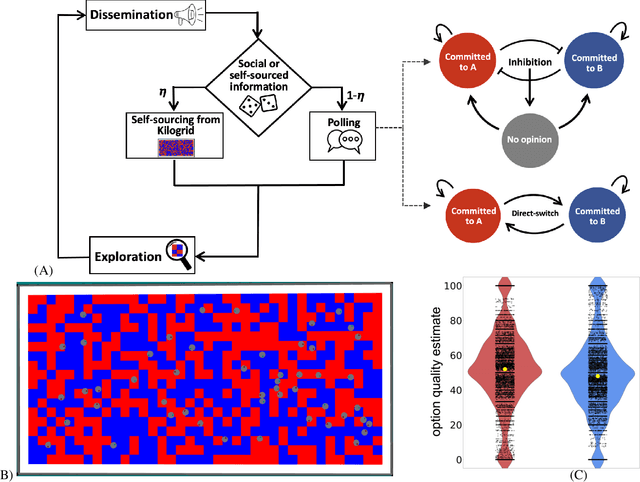
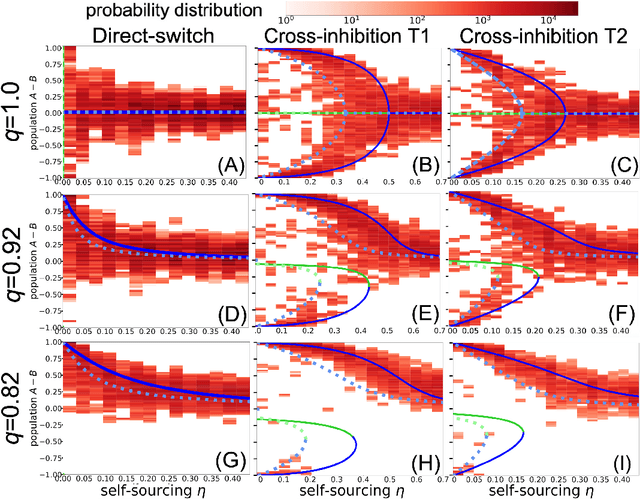
Abstract:Minimalistic robot swarms offer a scalable, robust, and cost-effective approach to performing complex tasks with the potential to transform applications in healthcare, disaster response, and environmental monitoring. However, coordinating such decentralised systems remains a fundamental challenge, particularly when robots are constrained in communication, computation, and memory. In our study, individual robots frequently make errors when sensing the environment, yet the swarm can rapidly and reliably reach consensus on the best among $n$ discrete options. We compare two canonical mechanisms of opinion dynamics -- direct-switch and cross-inhibition -- which are simple yet effective rules for collective information processing observed in biological systems across scales, from neural populations to insect colonies. We generalise the existing mean-field models by considering asocial biases influencing the opinion dynamics. While swarms using direct-switch reliably select the best option in absence of asocial dynamics, their performance deteriorates once such biases are introduced, often resulting in decision deadlocks. In contrast, bio-inspired cross-inhibition enables faster, more cohesive, accurate, robust, and scalable decisions across a wide range of biased conditions. Our findings provide theoretical and practical insights into the coordination of minimal swarms and offer insights that extend to a broad class of decentralised decision-making systems in biology and engineering.
Studying speed-accuracy trade-offs in best-of-n collective decision-making through heterogeneous mean-field modelling
Oct 20, 2023Abstract:To succeed in their objectives, groups of individuals must be able to make quick and accurate collective decisions on the best among alternatives with different qualities. Group-living animals aim to do that all the time. Plants and fungi are thought to do so too. Swarms of autonomous robots can also be programmed to make best-of-n decisions for solving tasks collaboratively. Ultimately, humans critically need it and so many times they should be better at it! Despite their simplicity, mathematical tractability made models like the voter model (VM) and the local majority rule model (MR) useful to describe in simple terms such collective decision-making processes. To reach a consensus, individuals change their opinion by interacting with neighbours in their social network. At least among animals and robots, options with a better quality are exchanged more often and therefore spread faster than lower-quality options, leading to the collective selection of the best option. With our work, we study the impact of individuals making errors in pooling others' opinions caused, for example, to reduce the cognitive load. Our analysis in grounded on the introduction of a model that generalises the two existing VM and MR models, showing a speed-accuracy trade-off regulated by the cognitive effort of individuals. We also investigate the impact of the interaction network topology on the collective dynamics. To do so, we extend our model and, by using the heterogeneous mean-field approach, we show that another speed-accuracy trade-off is regulated by network connectivity. An interesting result is that reduced network connectivity corresponds to an increase in collective decision accuracy
Recurrent Spectral Network (RSN): shaping the basin of attraction of a discrete map to reach automated classification
Feb 09, 2022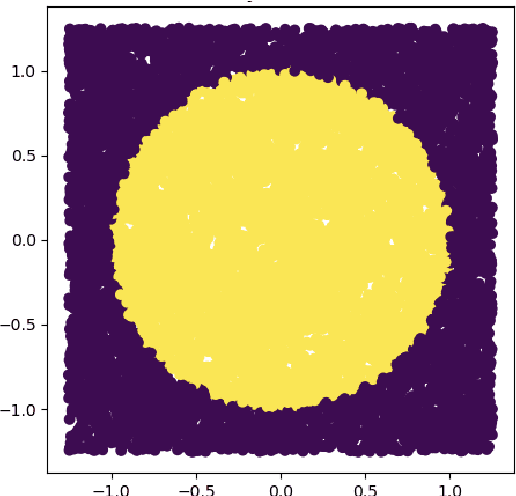
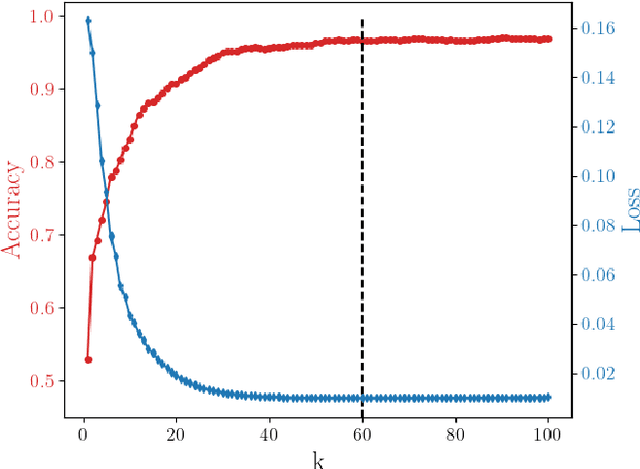
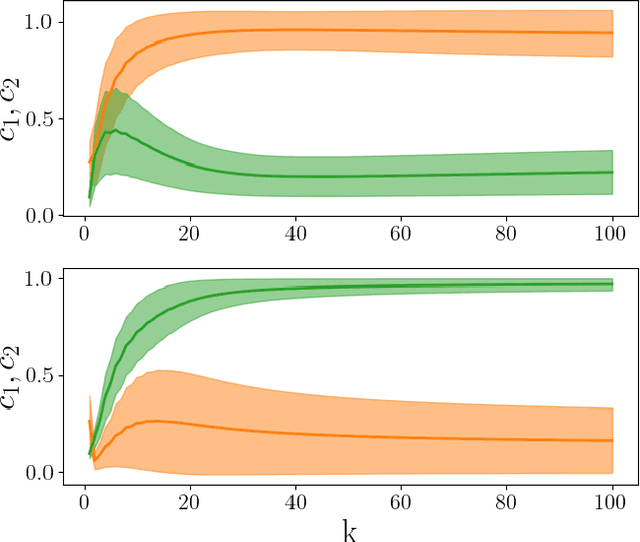
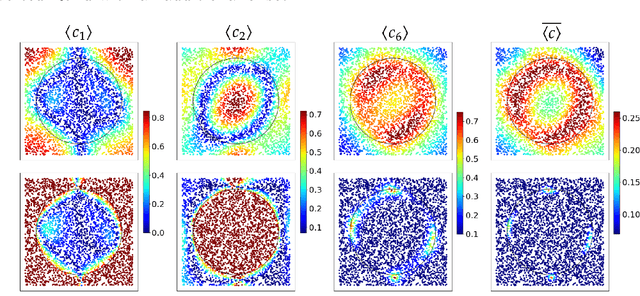
Abstract:A novel strategy to automated classification is introduced which exploits a fully trained dynamical system to steer items belonging to different categories toward distinct asymptotic attractors. These latter are incorporated into the model by taking advantage of the spectral decomposition of the operator that rules the linear evolution across the processing network. Non-linear terms act for a transient and allow to disentangle the data supplied as initial condition to the discrete dynamical system, shaping the boundaries of different attractors. The network can be equipped with several memory kernels which can be sequentially activated for serial datasets handling. Our novel approach to classification, that we here term Recurrent Spectral Network (RSN), is successfully challenged against a simple test-bed model, created for illustrative purposes, as well as a standard dataset for image processing training.
On the training of sparse and dense deep neural networks: less parameters, same performance
Jun 17, 2021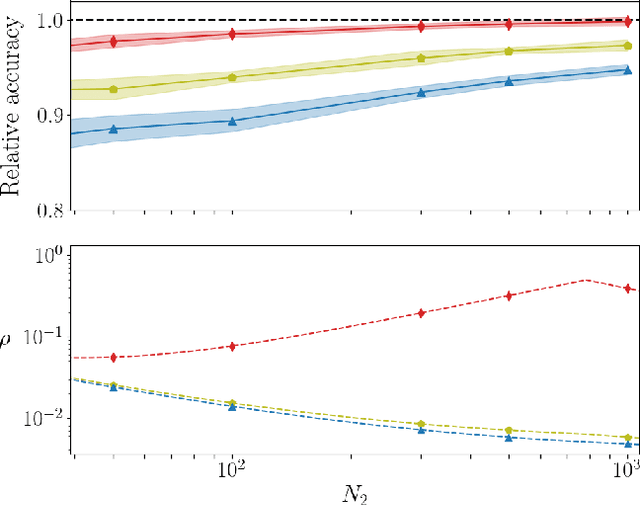
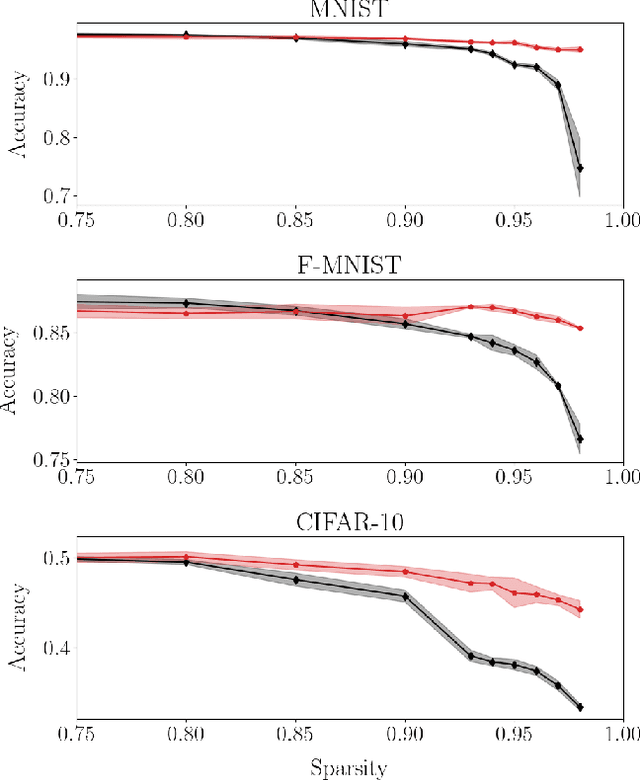
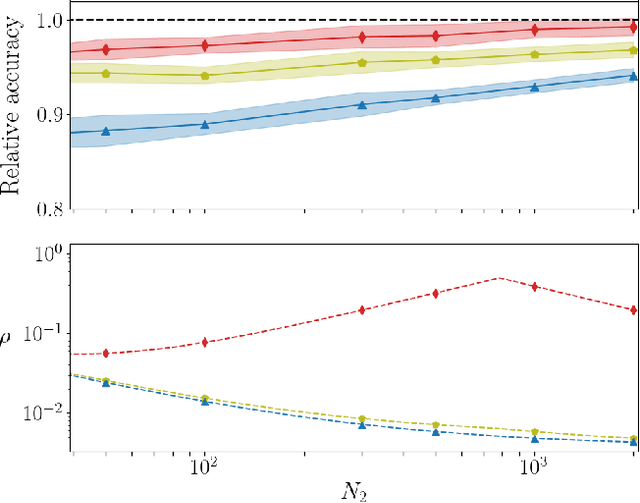
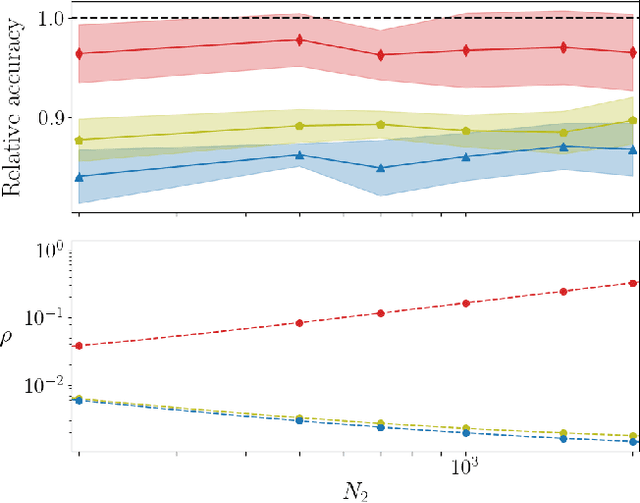
Abstract:Deep neural networks can be trained in reciprocal space, by acting on the eigenvalues and eigenvectors of suitable transfer operators in direct space. Adjusting the eigenvalues, while freezing the eigenvectors, yields a substantial compression of the parameter space. This latter scales by definition with the number of computing neurons. The classification scores, as measured by the displayed accuracy, are however inferior to those attained when the learning is carried in direct space, for an identical architecture and by employing the full set of trainable parameters (with a quadratic dependence on the size of neighbor layers). In this Letter, we propose a variant of the spectral learning method as appeared in Giambagli et al {Nat. Comm.} 2021, which leverages on two sets of eigenvalues, for each mapping between adjacent layers. The eigenvalues act as veritable knobs which can be freely tuned so as to (i) enhance, or alternatively silence, the contribution of the input nodes, (ii) modulate the excitability of the receiving nodes with a mechanism which we interpret as the artificial analogue of the homeostatic plasticity. The number of trainable parameters is still a linear function of the network size, but the performances of the trained device gets much closer to those obtained via conventional algorithms, these latter requiring however a considerably heavier computational cost. The residual gap between conventional and spectral trainings can be eventually filled by employing a suitable decomposition for the non trivial block of the eigenvectors matrix. Each spectral parameter reflects back on the whole set of inter-nodes weights, an attribute which we shall effectively exploit to yield sparse networks with stunning classification abilities, as compared to their homologues trained with conventional means.
Machine learning in spectral domain
May 29, 2020
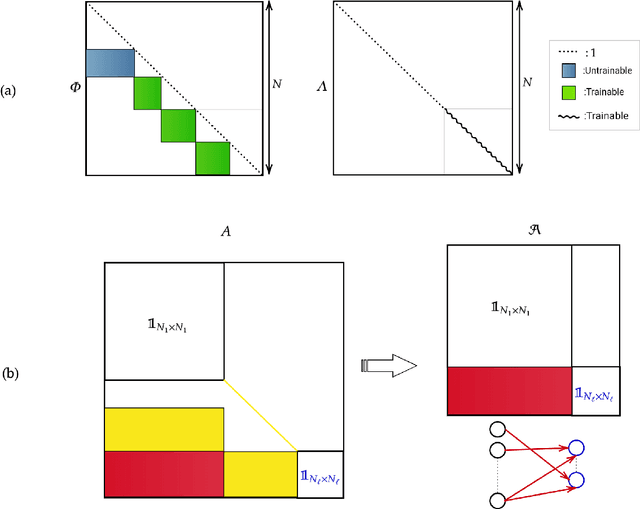
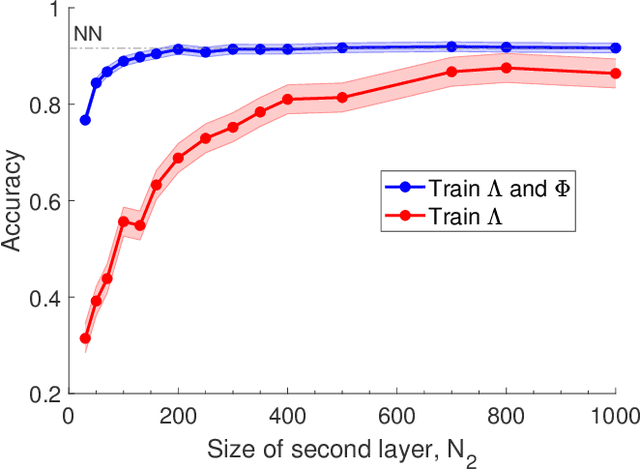
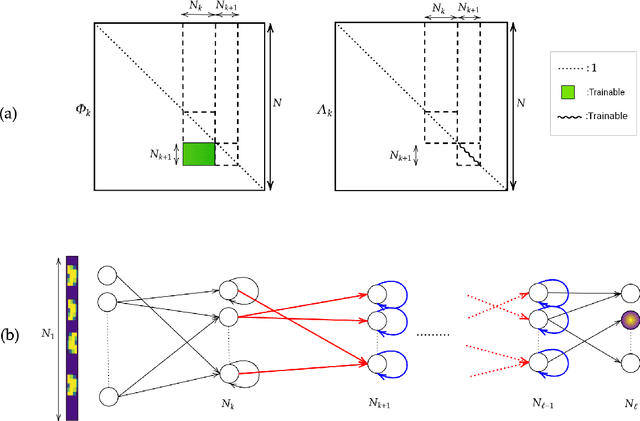
Abstract:Deep neural networks are usually trained in the space of the nodes, by adjusting the weights of existing links via suitable optimization protocols. We here propose a radically new approach which anchors the learning process to reciprocal space. Specifically, the training acts on the spectral domain and seeks to modify the eigenvectors and eigenvalues of transfer operators in direct space. The proposed method is ductile and can be tailored to return either linear or non linear classifiers. The performance are competitive with standard schemes, while allowing for a significant reduction of the learning parameter space. Spectral learning restricted to eigenvalues could be also employed for pre-training of the deep neural network, in conjunction with conventional machine-learning schemes. Further, it is surmised that the nested indentation of eigenvectors that defines the core idea of spectral learning could help understanding why deep networks work as well as they do.
Comparison of Discrete Choice Models and Artificial Neural Networks in Presence of Missing Variables
Nov 06, 2018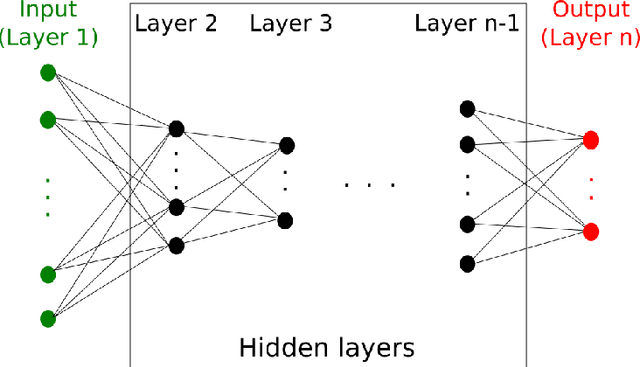

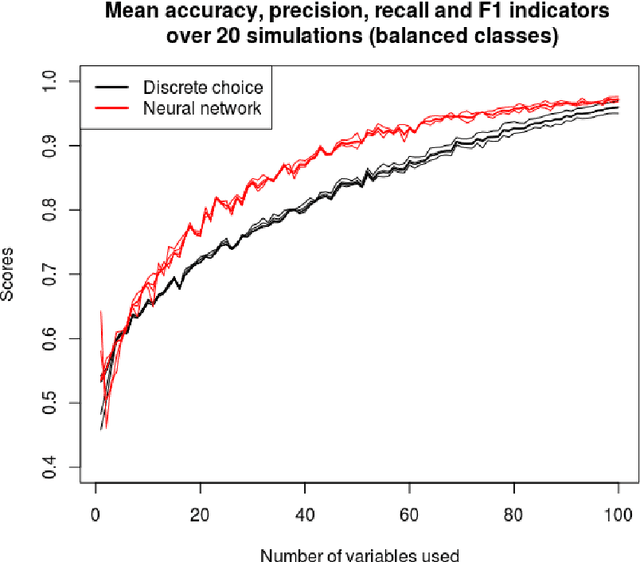
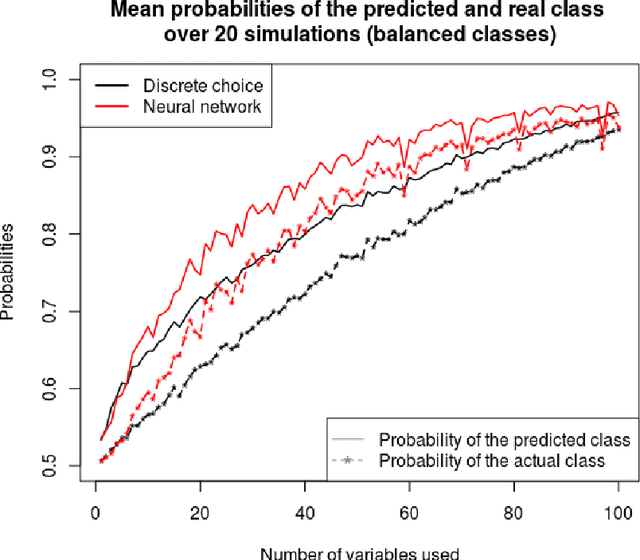
Abstract:Classification, the process of assigning a label (or class) to an observation given its features, is a common task in many applications. Nonetheless in most real-life applications, the labels can not be fully explained by the observed features. Indeed there can be many factors hidden to the modellers. The unexplained variation is then treated as some random noise which is handled differently depending on the method retained by the practitioner. This work focuses on two simple and widely used supervised classification algorithms: discrete choice models and artificial neural networks in the context of binary classification. Through various numerical experiments involving continuous or discrete explanatory features, we present a comparison of the retained methods' performance in presence of missing variables. The impact of the distribution of the two classes in the training data is also investigated. The outcomes of those experiments highlight the fact that artificial neural networks outperforms the discrete choice models, except when the distribution of the classes in the training data is highly unbalanced. Finally, this work provides some guidelines for choosing the right classifier with respect to the training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge