Lorenzo Giambagli
Spectral Architecture Search for Neural Networks
Apr 01, 2025Abstract:Architecture design and optimization are challenging problems in the field of artificial neural networks. Working in this context, we here present SPARCS (SPectral ARchiteCture Search), a novel architecture search protocol which exploits the spectral attributes of the inter-layer transfer matrices. SPARCS allows one to explore the space of possible architectures by spanning continuous and differentiable manifolds, thus enabling for gradient-based optimization algorithms to be eventually employed. With reference to simple benchmark models, we show that the newly proposed method yields a self-emerging architecture with a minimal degree of expressivity to handle the task under investigation and with a reduced parameter count as compared to other viable alternatives.
Learning in Wilson-Cowan model for metapopulation
Jun 24, 2024Abstract:The Wilson-Cowan model for metapopulation, a Neural Mass Network Model, treats different subcortical regions of the brain as connected nodes, with connections representing various types of structural, functional, or effective neuronal connectivity between these regions. Each region comprises interacting populations of excitatory and inhibitory cells, consistent with the standard Wilson-Cowan model. By incorporating stable attractors into such a metapopulation model's dynamics, we transform it into a learning algorithm capable of achieving high image and text classification accuracy. We test it on MNIST and Fashion MNIST, in combination with convolutional neural networks, on CIFAR-10 and TF-FLOWERS, and, in combination with a transformer architecture (BERT), on IMDB, always showing high classification accuracy. These numerical evaluations illustrate that minimal modifications to the Wilson-Cowan model for metapopulation can reveal unique and previously unobserved dynamics.
Automatic Input Feature Relevance via Spectral Neural Networks
Jun 03, 2024Abstract:Working with high-dimensional data is a common practice, in the field of machine learning. Identifying relevant input features is thus crucial, so as to obtain compact dataset more prone for effective numerical handling. Further, by isolating pivotal elements that form the basis of decision making, one can contribute to elaborate on - ex post - models' interpretability, so far rather elusive. Here, we propose a novel method to estimate the relative importance of the input components for a Deep Neural Network. This is achieved by leveraging on a spectral re-parametrization of the optimization process. Eigenvalues associated to input nodes provide in fact a robust proxy to gauge the relevance of the supplied entry features. Unlike existing techniques, the spectral features ranking is carried out automatically, as a byproduct of the network training. The technique is successfully challenged against both synthetic and real data.
Engineered Ordinary Differential Equations as Classification Algorithm (EODECA): thorough characterization and testing
Dec 22, 2023Abstract:EODECA (Engineered Ordinary Differential Equations as Classification Algorithm) is a novel approach at the intersection of machine learning and dynamical systems theory, presenting a unique framework for classification tasks [1]. This method stands out with its dynamical system structure, utilizing ordinary differential equations (ODEs) to efficiently handle complex classification challenges. The paper delves into EODECA's dynamical properties, emphasizing its resilience against random perturbations and robust performance across various classification scenarios. Notably, EODECA's design incorporates the ability to embed stable attractors in the phase space, enhancing reliability and allowing for reversible dynamics. In this paper, we carry out a comprehensive analysis by expanding on the work [1], and employing a Euler discretization scheme. In particular, we evaluate EODECA's performance across five distinct classification problems, examining its adaptability and efficiency. Significantly, we demonstrate EODECA's effectiveness on the MNIST and Fashion MNIST datasets, achieving impressive accuracies of $98.06\%$ and $88.21\%$, respectively. These results are comparable to those of a multi-layer perceptron (MLP), underscoring EODECA's potential in complex data processing tasks. We further explore the model's learning journey, assessing its evolution in both pre and post training environments and highlighting its ability to navigate towards stable attractors. The study also investigates the invertibility of EODECA, shedding light on its decision-making processes and internal workings. This paper presents a significant step towards a more transparent and robust machine learning paradigm, bridging the gap between machine learning algorithms and dynamical systems methodologies.
Complex Recurrent Spectral Network
Dec 12, 2023Abstract:This paper presents a novel approach to advancing artificial intelligence (AI) through the development of the Complex Recurrent Spectral Network ($\mathbb{C}$-RSN), an innovative variant of the Recurrent Spectral Network (RSN) model. The $\mathbb{C}$-RSN is designed to address a critical limitation in existing neural network models: their inability to emulate the complex processes of biological neural networks dynamically and accurately. By integrating key concepts from dynamical systems theory and leveraging principles from statistical mechanics, the $\mathbb{C}$-RSN model introduces localized non-linearity, complex fixed eigenvalues, and a distinct separation of memory and input processing functionalities. These features collectively enable the $\mathbb{C}$-RSN evolving towards a dynamic, oscillating final state that more closely mirrors biological cognition. Central to this work is the exploration of how the $\mathbb{C}$-RSN manages to capture the rhythmic, oscillatory dynamics intrinsic to biological systems, thanks to its complex eigenvalue structure and the innovative segregation of its linear and non-linear components. The model's ability to classify data through a time-dependent function, and the localization of information processing, is demonstrated with an empirical evaluation using the MNIST dataset. Remarkably, distinct items supplied as a sequential input yield patterns in time which bear the indirect imprint of the insertion order (and of the time of separation between contiguous insertions).
A Bridge between Dynamical Systems and Machine Learning: Engineered Ordinary Differential Equations as Classification Algorithm (EODECA)
Nov 17, 2023Abstract:In a world increasingly reliant on machine learning, the interpretability of these models remains a substantial challenge, with many equating their functionality to an enigmatic black box. This study seeks to bridge machine learning and dynamical systems. Recognizing the deep parallels between dense neural networks and dynamical systems, particularly in the light of non-linearities and successive transformations, this manuscript introduces the Engineered Ordinary Differential Equations as Classification Algorithms (EODECAs). Uniquely designed as neural networks underpinned by continuous ordinary differential equations, EODECAs aim to capitalize on the well-established toolkit of dynamical systems. Unlike traditional deep learning models, which often suffer from opacity, EODECAs promise both high classification performance and intrinsic interpretability. They are naturally invertible, granting them an edge in understanding and transparency over their counterparts. By bridging these domains, we hope to usher in a new era of machine learning models where genuine comprehension of data processes complements predictive prowess.
How a student becomes a teacher: learning and forgetting through Spectral methods
Nov 03, 2023Abstract:In theoretical ML, the teacher-student paradigm is often employed as an effective metaphor for real-life tuition. The above scheme proves particularly relevant when the student network is overparameterized as compared to the teacher network. Under these operating conditions, it is tempting to speculate that the student ability to handle the given task could be eventually stored in a sub-portion of the whole network. This latter should be to some extent reminiscent of the frozen teacher structure, according to suitable metrics, while being approximately invariant across different architectures of the student candidate network. Unfortunately, state-of-the-art conventional learning techniques could not help in identifying the existence of such an invariant subnetwork, due to the inherent degree of non-convexity that characterizes the examined problem. In this work, we take a leap forward by proposing a radically different optimization scheme which builds on a spectral representation of the linear transfer of information between layers. The gradient is hence calculated with respect to both eigenvalues and eigenvectors with negligible increase in terms of computational and complexity load, as compared to standard training algorithms. Working in this framework, we could isolate a stable student substructure, that mirrors the true complexity of the teacher in terms of computing neurons, path distribution and topological attributes. When pruning unimportant nodes of the trained student, as follows a ranking that reflects the optimized eigenvalues, no degradation in the recorded performance is seen above a threshold that corresponds to the effective teacher size. The observed behavior can be pictured as a genuine second-order phase transition that bears universality traits.
* 10 pages + references + supplemental material. Poster presentation at NeurIPS 2023
Recurrent Spectral Network (RSN): shaping the basin of attraction of a discrete map to reach automated classification
Feb 09, 2022
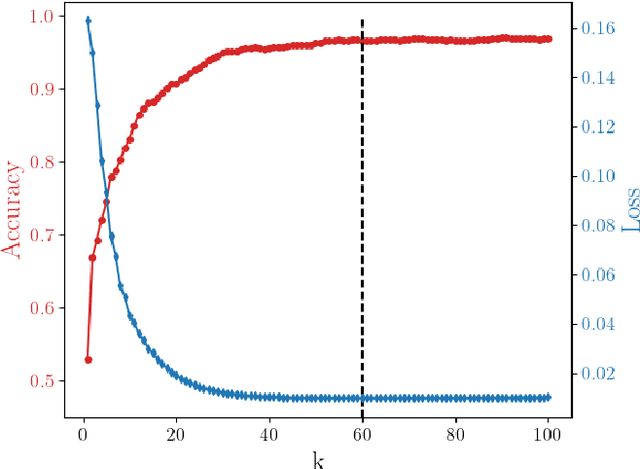
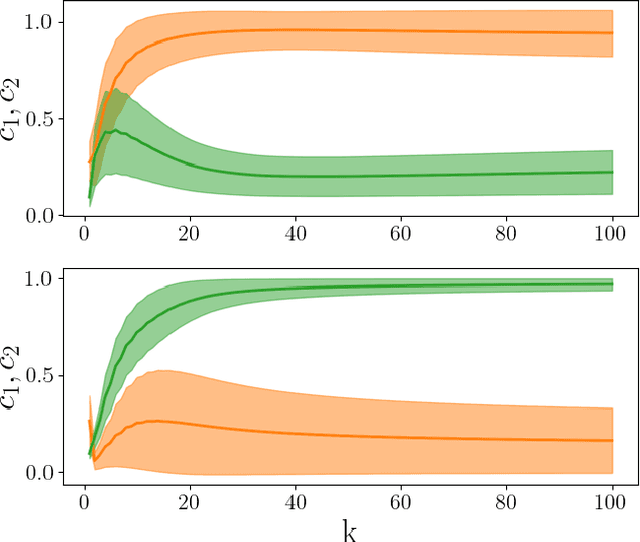
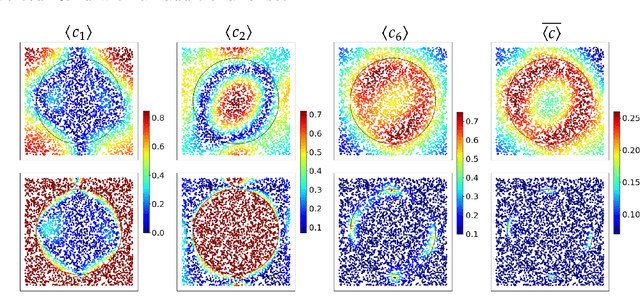
Abstract:A novel strategy to automated classification is introduced which exploits a fully trained dynamical system to steer items belonging to different categories toward distinct asymptotic attractors. These latter are incorporated into the model by taking advantage of the spectral decomposition of the operator that rules the linear evolution across the processing network. Non-linear terms act for a transient and allow to disentangle the data supplied as initial condition to the discrete dynamical system, shaping the boundaries of different attractors. The network can be equipped with several memory kernels which can be sequentially activated for serial datasets handling. Our novel approach to classification, that we here term Recurrent Spectral Network (RSN), is successfully challenged against a simple test-bed model, created for illustrative purposes, as well as a standard dataset for image processing training.
On the training of sparse and dense deep neural networks: less parameters, same performance
Jun 17, 2021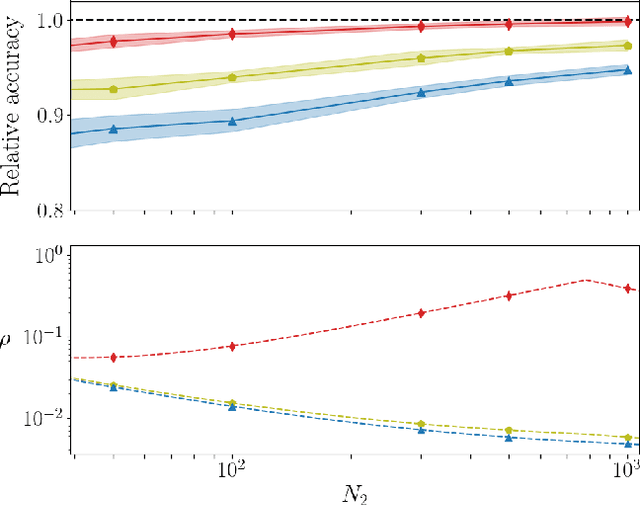
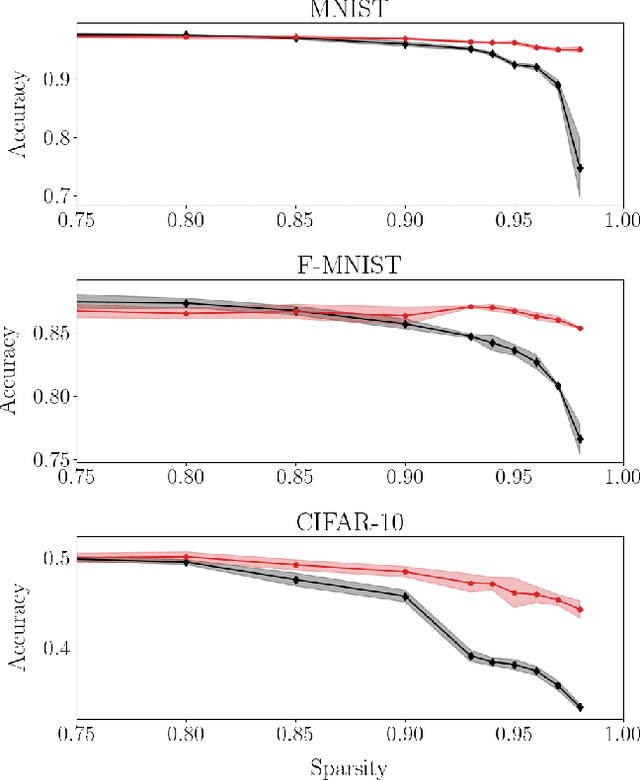
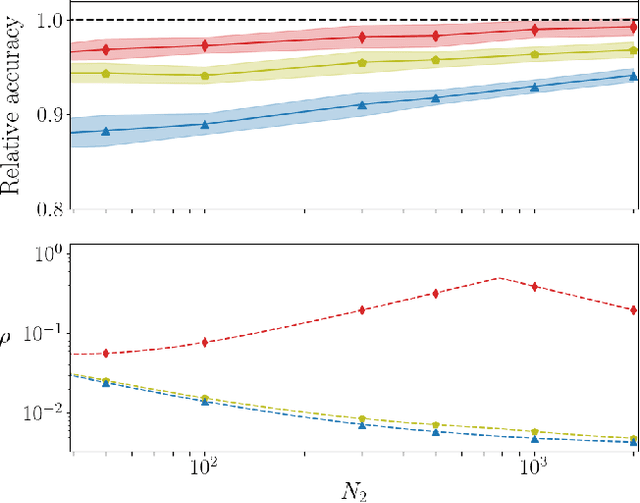
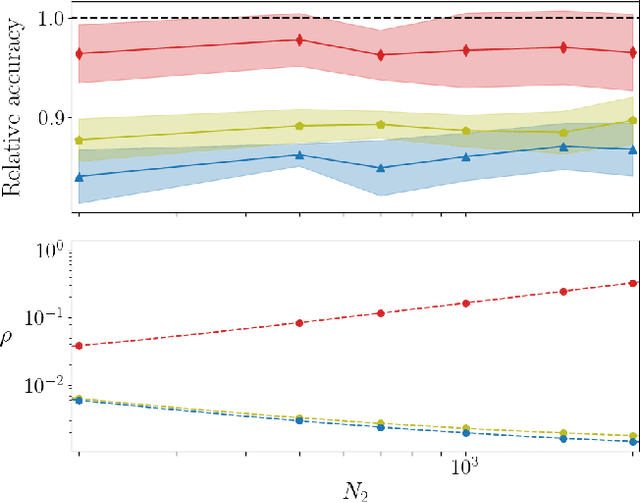
Abstract:Deep neural networks can be trained in reciprocal space, by acting on the eigenvalues and eigenvectors of suitable transfer operators in direct space. Adjusting the eigenvalues, while freezing the eigenvectors, yields a substantial compression of the parameter space. This latter scales by definition with the number of computing neurons. The classification scores, as measured by the displayed accuracy, are however inferior to those attained when the learning is carried in direct space, for an identical architecture and by employing the full set of trainable parameters (with a quadratic dependence on the size of neighbor layers). In this Letter, we propose a variant of the spectral learning method as appeared in Giambagli et al {Nat. Comm.} 2021, which leverages on two sets of eigenvalues, for each mapping between adjacent layers. The eigenvalues act as veritable knobs which can be freely tuned so as to (i) enhance, or alternatively silence, the contribution of the input nodes, (ii) modulate the excitability of the receiving nodes with a mechanism which we interpret as the artificial analogue of the homeostatic plasticity. The number of trainable parameters is still a linear function of the network size, but the performances of the trained device gets much closer to those obtained via conventional algorithms, these latter requiring however a considerably heavier computational cost. The residual gap between conventional and spectral trainings can be eventually filled by employing a suitable decomposition for the non trivial block of the eigenvectors matrix. Each spectral parameter reflects back on the whole set of inter-nodes weights, an attribute which we shall effectively exploit to yield sparse networks with stunning classification abilities, as compared to their homologues trained with conventional means.
Machine learning in spectral domain
May 29, 2020
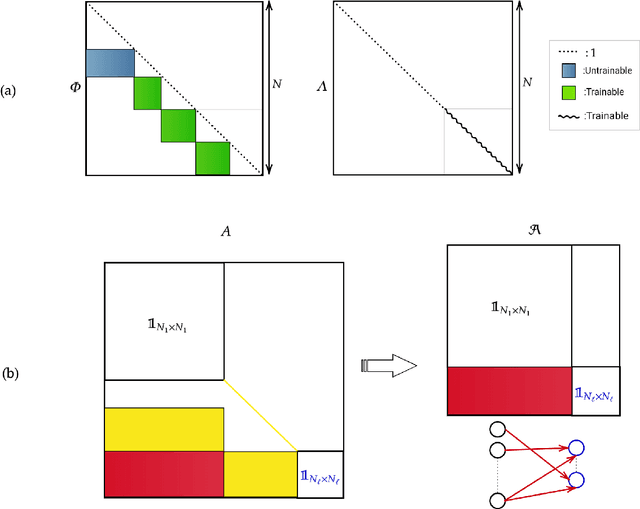
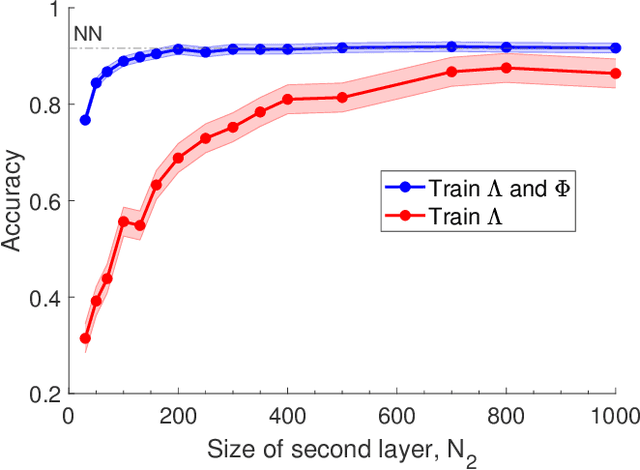
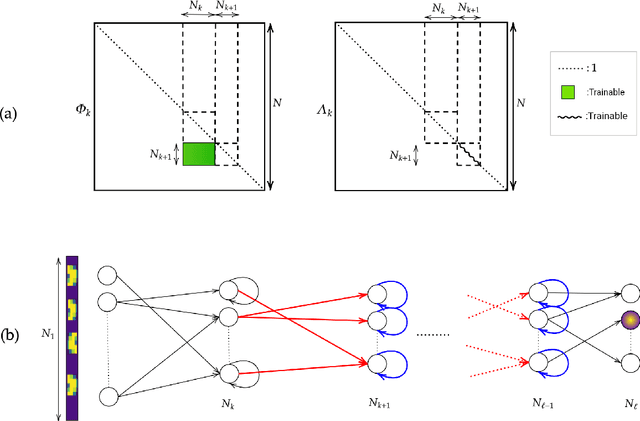
Abstract:Deep neural networks are usually trained in the space of the nodes, by adjusting the weights of existing links via suitable optimization protocols. We here propose a radically new approach which anchors the learning process to reciprocal space. Specifically, the training acts on the spectral domain and seeks to modify the eigenvectors and eigenvalues of transfer operators in direct space. The proposed method is ductile and can be tailored to return either linear or non linear classifiers. The performance are competitive with standard schemes, while allowing for a significant reduction of the learning parameter space. Spectral learning restricted to eigenvalues could be also employed for pre-training of the deep neural network, in conjunction with conventional machine-learning schemes. Further, it is surmised that the nested indentation of eigenvectors that defines the core idea of spectral learning could help understanding why deep networks work as well as they do.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge