Towards an Optimal Control Perspective of ResNet Training

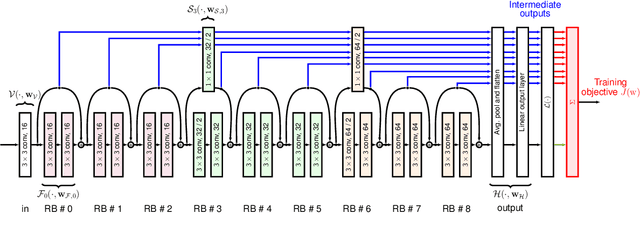
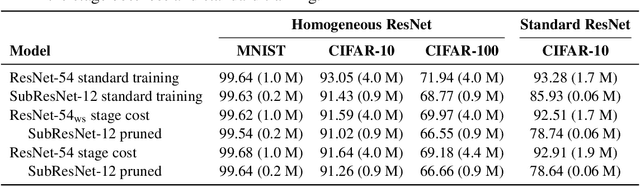
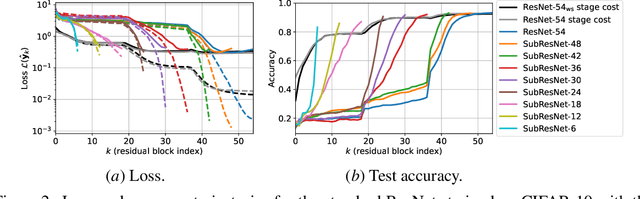
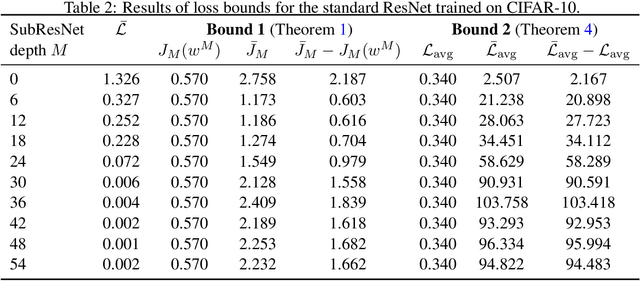
We propose a training formulation for ResNets reflecting an optimal control problem that is applicable for standard architectures and general loss functions. We suggest bridging both worlds via penalizing intermediate outputs of hidden states corresponding to stage cost terms in optimal control. For standard ResNets, we obtain intermediate outputs by propagating the state through the subsequent skip connections and the output layer. We demonstrate that our training dynamic biases the weights of the unnecessary deeper residual layers to vanish. This indicates the potential for a theory-grounded layer pruning strategy.

Towards safe Bayesian optimization with Wiener kernel regression

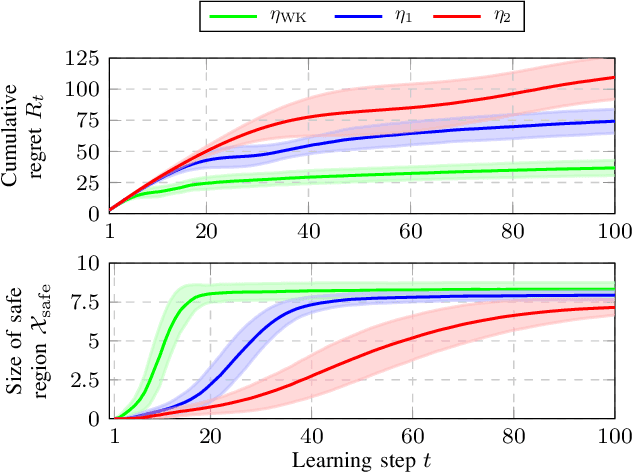
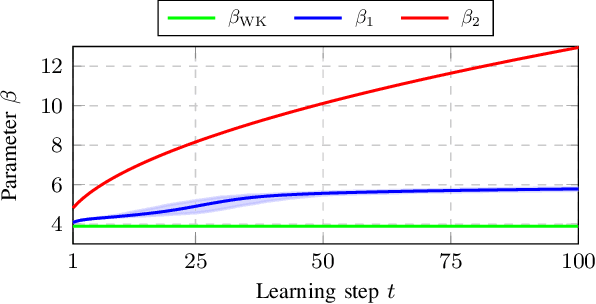
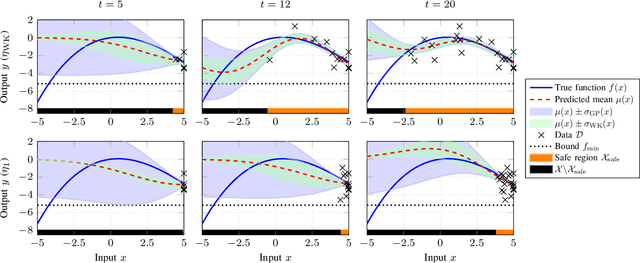
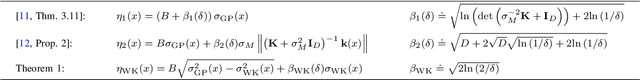
Bayesian Optimization (BO) is a data-driven strategy for minimizing/maximizing black-box functions based on probabilistic surrogate models. In the presence of safety constraints, the performance of BO crucially relies on tight probabilistic error bounds related to the uncertainty surrounding the surrogate model. For the case of Gaussian Process surrogates and Gaussian measurement noise, we present a novel error bound based on the recently proposed Wiener kernel regression. We prove that under rather mild assumptions, the proposed error bound is tighter than bounds previously documented in the literature which leads to enlarged safety regions. We draw upon a numerical example to demonstrate the efficacy of the proposed error bound in safe BO.

On Dissipativity of Cross-Entropy Loss in Training ResNets

The training of ResNets and neural ODEs can be formulated and analyzed from the perspective of optimal control. This paper proposes a dissipative formulation of the training of ResNets and neural ODEs for classification problems by including a variant of the cross-entropy as a regularization in the stage cost. Based on the dissipative formulation of the training, we prove that the trained ResNet exhibit the turnpike phenomenon. We then illustrate that the training exhibits the turnpike phenomenon by training on the two spirals and MNIST datasets. This can be used to find very shallow networks suitable for a given classification task.

Exploring the Links between the Fundamental Lemma and Kernel Regression

Generalizations and variations of the fundamental lemma by Willems et al. are an active topic of recent research. In this note, we explore and formalize the links between kernel regression and known nonlinear extensions of the fundamental lemma. Applying a transformation to the usual linear equation in Hankel matrices, we arrive at an alternative implicit kernel representation of the system trajectories while keeping the requirements on persistency of excitation. We show that this representation is equivalent to the solution of a specific kernel regression problem. We explore the possible structures of the underlying kernel as well as the system classes to which they correspond.

Cooperative Distributed MPC via Decentralized Real-Time Optimization: Implementation Results for Robot Formations

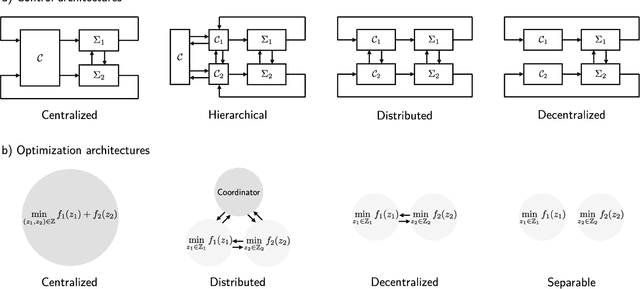
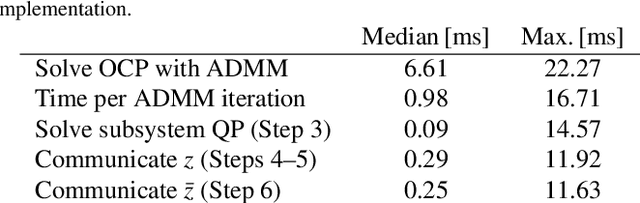
Distributed model predictive control (DMPC) is a flexible and scalable feedback control method applicable to a wide range of systems. While stability analysis of DMPC is quite well understood, there exist only limited implementation results for realistic applications involving distributed computation and networked communication. This article approaches formation control of mobile robots via a cooperative DMPC scheme. We discuss the implementation via decentralized optimization algorithms. To this end, we combine the alternating direction method of multipliers with decentralized sequential quadratic programming to solve the underlying optimal control problem in a decentralized fashion. Our approach only requires coupled subsystems to communicate and does not rely on a central coordinator. Our experimental results showcase the efficacy of DMPC for formation control and they demonstrate the real-time feasibility of the considered algorithms.

On the Turnpike to Design of Deep Neural Nets: Explicit Depth Bounds

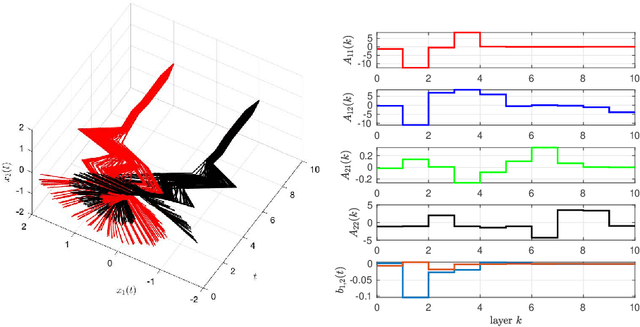
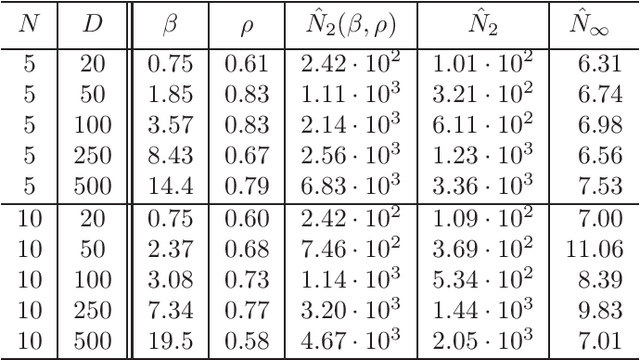
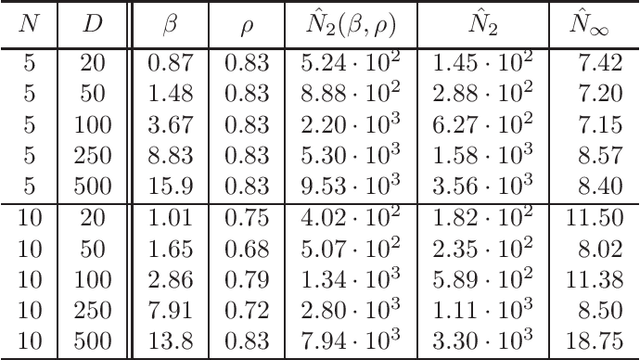
It is well-known that the training of Deep Neural Networks (DNN) can be formalized in the language of optimal control. In this context, this paper leverages classical turnpike properties of optimal control problems to attempt a quantifiable answer to the question of how many layers should be considered in a DNN. The underlying assumption is that the number of neurons per layer -- i.e., the width of the DNN -- is kept constant. Pursuing a different route than the classical analysis of approximation properties of sigmoidal functions, we prove explicit bounds on the required depths of DNNs based on asymptotic reachability assumptions and a dissipativity-inducing choice of the regularization terms in the training problem. Numerical results obtained for the two spiral task data set for classification indicate that the proposed estimates can provide non-conservative depth bounds.