On Uniform Error Bounds for Kernel Regression under Non-Gaussian Noise

Providing non-conservative uncertainty quantification for function estimates derived from noisy observations remains a fundamental challenge in statistical machine learning, particularly for applications in safety-critical domains. In this work, we propose novel non-asymptotic probabilistic uniform error bounds for kernel-based regression. Compared to related bounds in the literature that are restricted to (conditionally) independent sub-Gaussian noise, our bounds allow to consider a broad class of non-Gaussian distributions, such as sub-Gaussian, bounded, sub-exponential, and variance/moment-bounded noise. Moreover, our results apply to correlated and uncorrelated noise. We compare our proposed error bounds with existing results in terms of the induced uncertainty region and their performance in safe control, demonstrating the tightness of the proposed bounds.

Towards safe Bayesian optimization with Wiener kernel regression

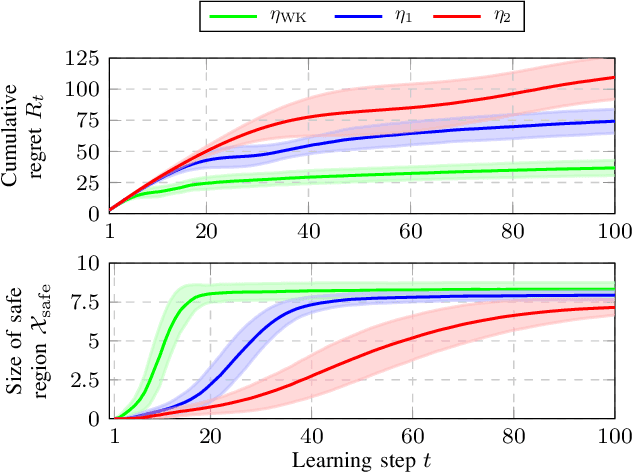
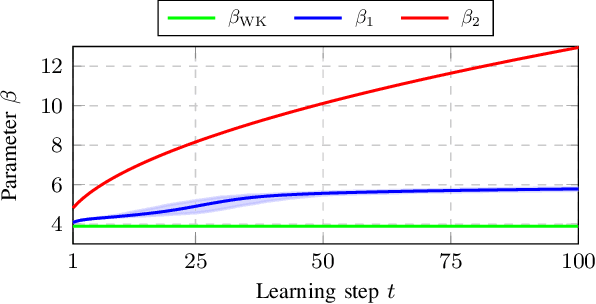
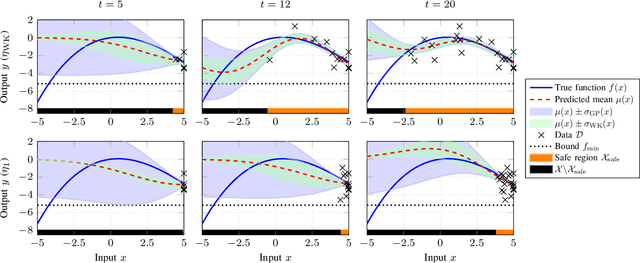
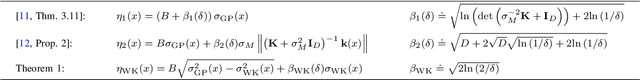
Bayesian Optimization (BO) is a data-driven strategy for minimizing/maximizing black-box functions based on probabilistic surrogate models. In the presence of safety constraints, the performance of BO crucially relies on tight probabilistic error bounds related to the uncertainty surrounding the surrogate model. For the case of Gaussian Process surrogates and Gaussian measurement noise, we present a novel error bound based on the recently proposed Wiener kernel regression. We prove that under rather mild assumptions, the proposed error bound is tighter than bounds previously documented in the literature which leads to enlarged safety regions. We draw upon a numerical example to demonstrate the efficacy of the proposed error bound in safe BO.

Exploring the Links between the Fundamental Lemma and Kernel Regression

Generalizations and variations of the fundamental lemma by Willems et al. are an active topic of recent research. In this note, we explore and formalize the links between kernel regression and known nonlinear extensions of the fundamental lemma. Applying a transformation to the usual linear equation in Hankel matrices, we arrive at an alternative implicit kernel representation of the system trajectories while keeping the requirements on persistency of excitation. We show that this representation is equivalent to the solution of a specific kernel regression problem. We explore the possible structures of the underlying kernel as well as the system classes to which they correspond.