Experimental verification of an online traction parameter identification method

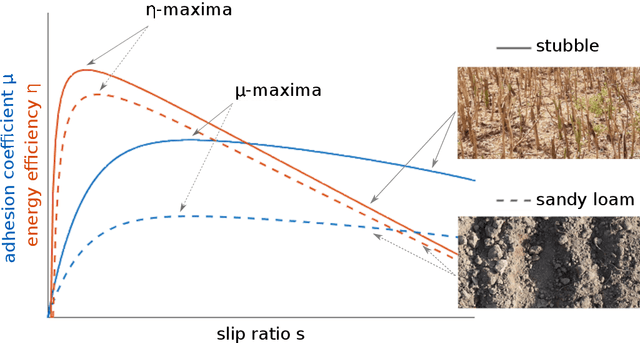
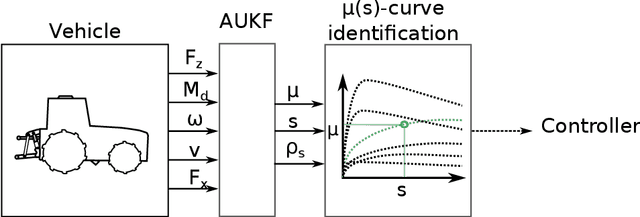
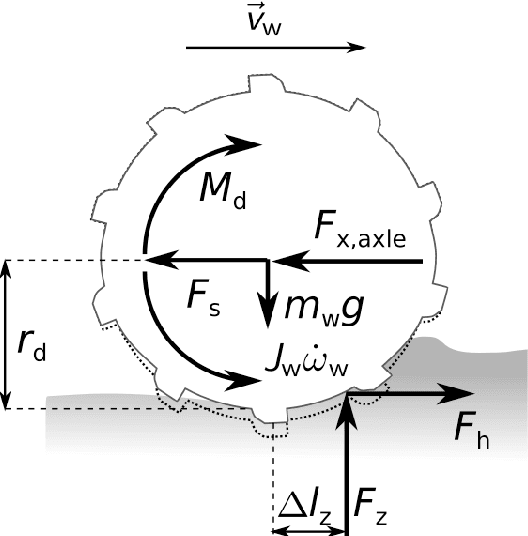
Traction parameters, that characterize the ground-wheel contact dynamics, are the central factor in the energy efficiency of vehicles. To optimize fuel consumption, reduce wear of tires, increase productivity etc., knowledge of current traction parameters is unavoidable. Unfortunately, these parameters are difficult to measure and require expensive force and torque sensors. An alternative way is to use system identification to determine them. In this work, we validate such a method in field experiments with a mobile robot. The method is based on an adaptive Kalman filter. We show how it estimates the traction parameters online, during the motion on the field, and compare them to their values determined via a 6-directional force-torque sensor installed for verification. Data of adhesion slip ratio curves is recorded and compared to curves from literature for additional validation of the method. The results can establish a foundation for a number of optimal traction methods.

A stabilizing reinforcement learning approach for sampled systems with partially unknown models

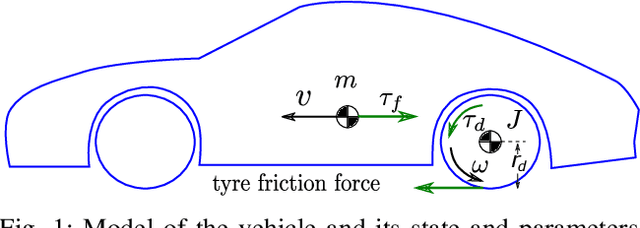
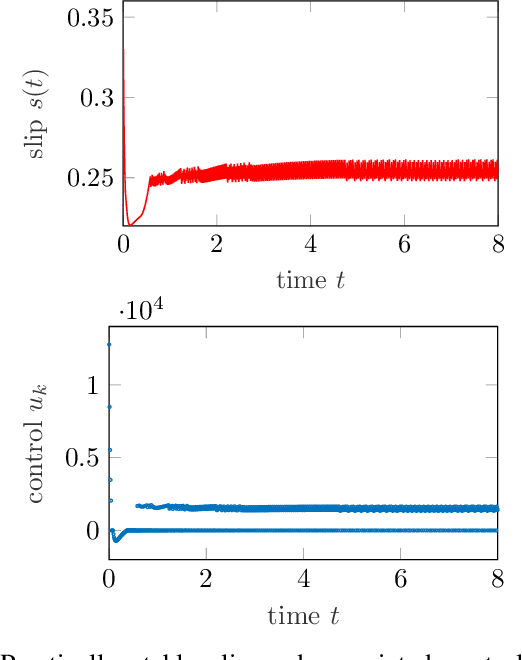
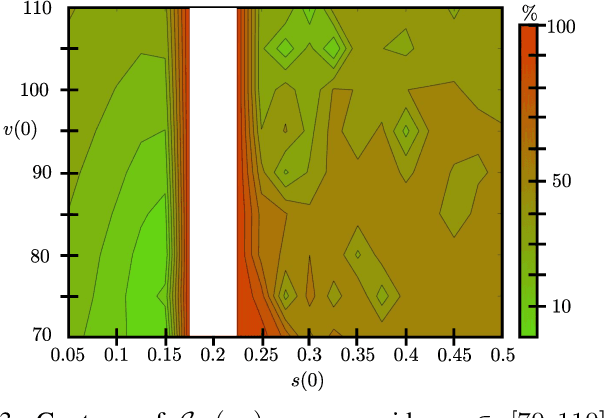
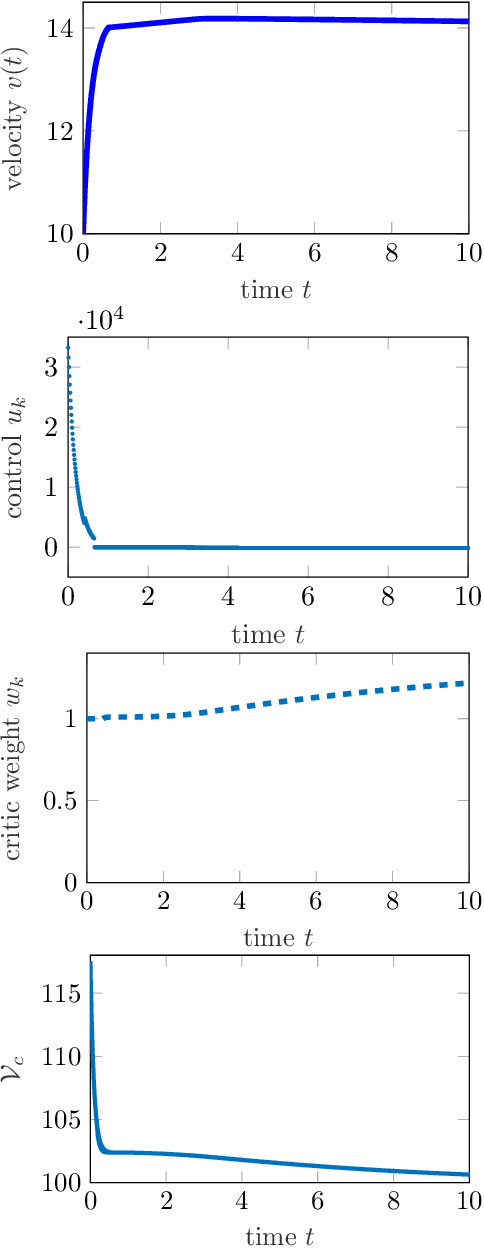
Reinforcement learning is commonly associated with training of reward-maximizing (or cost-minimizing) agents, in other words, controllers. It can be applied in model-free or model-based fashion, using a priori or online collected system data to train involved parametric architectures. In general, online reinforcement learning does not guarantee closed loop stability unless special measures are taken, for instance, through learning constraints or tailored training rules. Particularly promising are hybrids of reinforcement learning with "classical" control approaches. In this work, we suggest a method to guarantee practical stability of the system-controller closed loop in a purely online learning setting, i.e., without offline training. Moreover, we assume only partial knowledge of the system model. To achieve the claimed results, we employ techniques of classical adaptive control. The implementation of the overall control scheme is provided explicitly in a digital, sampled setting. That is, the controller receives the state of the system and computes the control action at discrete, specifically, equidistant moments in time. The method is tested in adaptive traction control and cruise control where it proved to significantly reduce the cost.

On the Turnpike to Design of Deep Neural Nets: Explicit Depth Bounds

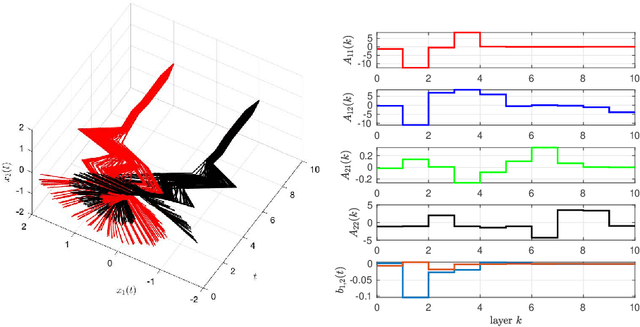
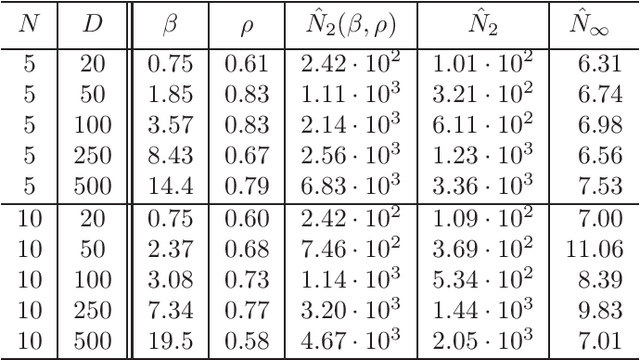
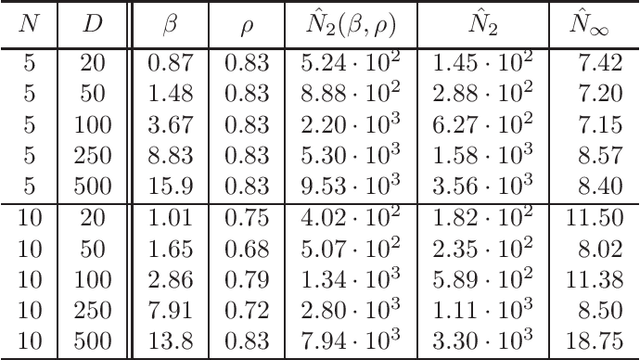
It is well-known that the training of Deep Neural Networks (DNN) can be formalized in the language of optimal control. In this context, this paper leverages classical turnpike properties of optimal control problems to attempt a quantifiable answer to the question of how many layers should be considered in a DNN. The underlying assumption is that the number of neurons per layer -- i.e., the width of the DNN -- is kept constant. Pursuing a different route than the classical analysis of approximation properties of sigmoidal functions, we prove explicit bounds on the required depths of DNNs based on asymptotic reachability assumptions and a dissipativity-inducing choice of the regularization terms in the training problem. Numerical results obtained for the two spiral task data set for classification indicate that the proposed estimates can provide non-conservative depth bounds.