Tim Pfeifer
A Credible and Robust approach to Ego-Motion Estimation using an Automotive Radar
Apr 19, 2022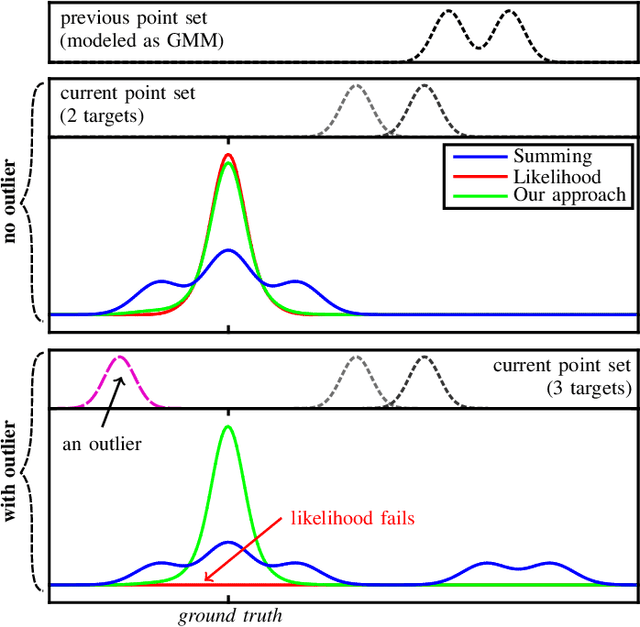
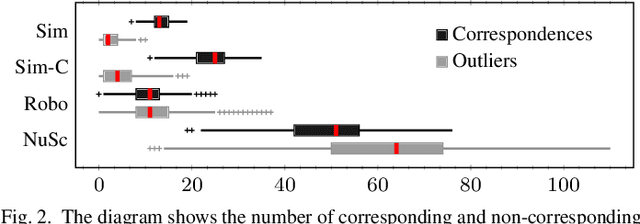
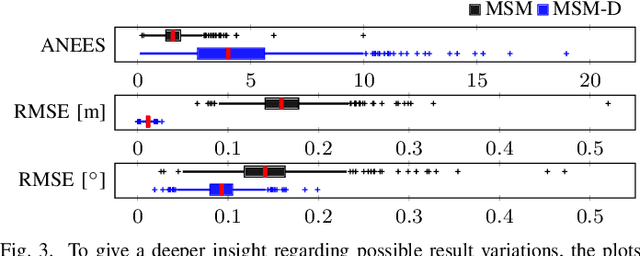
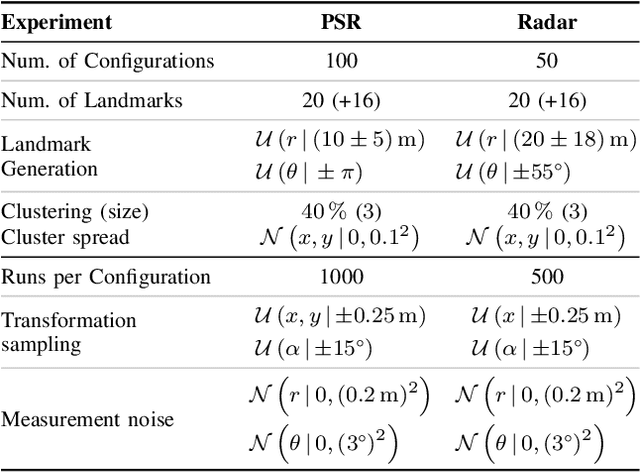
Abstract:Consistent motion estimation is fundamental for all mobile autonomous systems. While this sounds like an easy task, often, it is not the case because of changing environmental conditions affecting odometry obtained from vision, Lidar, or the wheels themselves. Unsusceptible to challenging lighting and weather conditions, radar sensors are an obvious alternative. Usually, automotive radars return a sparse point cloud, representing the surroundings. Utilizing this information to motion estimation is challenging due to unstable and phantom measurements, which result in a high rate of outliers. We introduce a credible and robust probabilistic approach to estimate the ego-motion based on these challenging radar measurements; intended to be used within a loosely-coupled sensor fusion framework. Compared to existing solutions, evaluated on the popular nuScenes dataset and others, we show that our proposed algorithm is more credible while not depending on explicit correspondence calculation.
Advancing Mixture Models for Least Squares Optimization
Apr 01, 2021


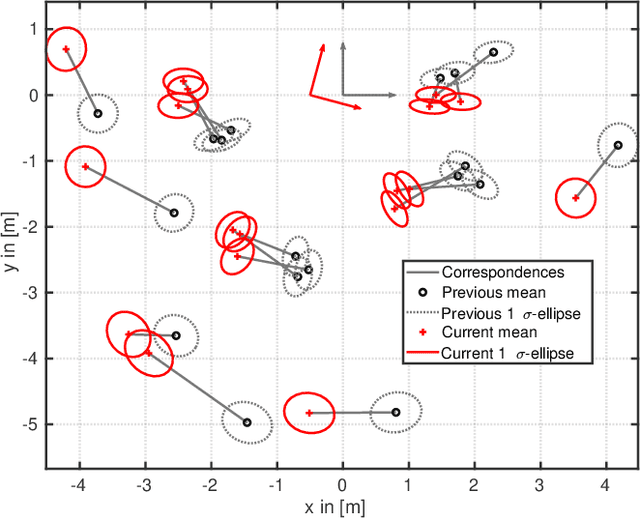
Abstract:Gaussian mixtures are a powerful and widely used tool to model non-Gaussian estimation problems. They are able to describe measurement errors that follow arbitrary distributions and can represent ambiguity in assignment tasks like point set registration or tracking. However, using them with common least squares solvers is still difficult. Existing approaches are either approximations of the true mixture or prone to convergence issues due to their strong nonlinearity. We propose a novel least squares representation of a Gaussian mixture, which is an exact and almost linear model of the corresponding log-likelihood. Our approach provides an efficient, accurate and flexible model for many probabilistic estimation problems and can be used as cost function for least squares solvers. We demonstrate its superior performance in various Monte Carlo experiments, including different kinds of point set registration. Our implementation is available as open source code for the state-of-the-art solvers Ceres and GTSAM.
Factor Graph based 3D Multi-Object Tracking in Point Clouds
Aug 12, 2020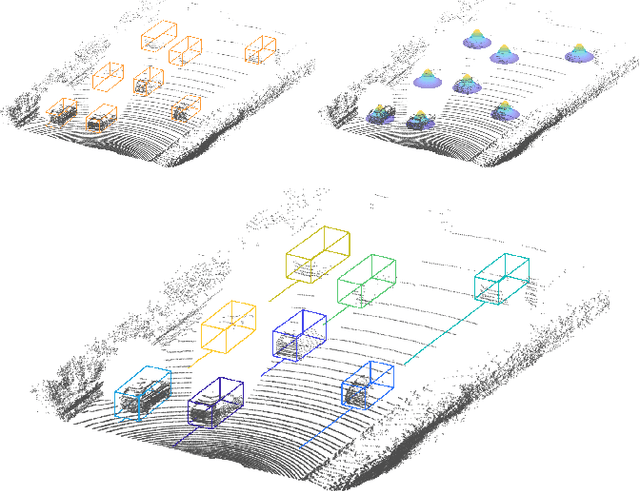
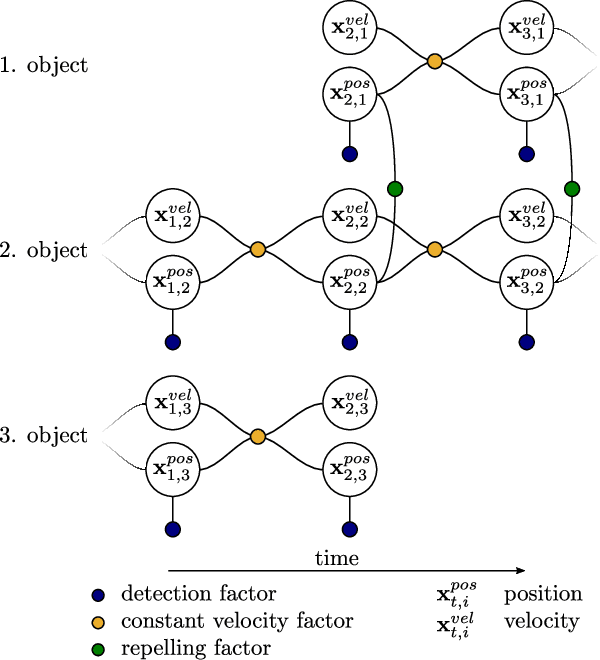
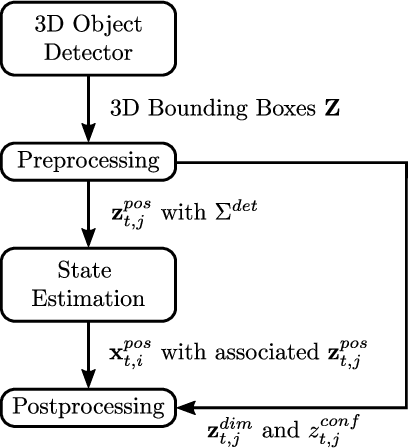

Abstract:Accurate and reliable tracking of multiple moving objects in 3D space is an essential component of urban scene understanding. This is a challenging task because it requires the assignment of detections in the current frame to the predicted objects from the previous one. Existing filter-based approaches tend to struggle if this initial assignment is not correct, which can happen easily. We propose a novel optimization-based approach that does not rely on explicit and fixed assignments. Instead, we represent the result of an off-the-shelf 3D object detector as Gaussian mixture model, which is incorporated in a factor graph framework. This gives us the flexibility to assign all detections to all objects simultaneously. As a result, the assignment problem is solved implicitly and jointly with the 3D spatial multi-object state estimation using non-linear least squares optimization. Despite its simplicity, the proposed algorithm achieves robust and reliable tracking results and can be applied for offline as well as online tracking. We demonstrate its performance on the real world KITTI tracking dataset and achieve better results than many state-of-the-art algorithms. Especially the consistency of the estimated tracks is superior offline as well as online.
It is time for Factor Graph Optimization for GNSS/INS Integration: Comparison between FGO and EKF
Apr 24, 2020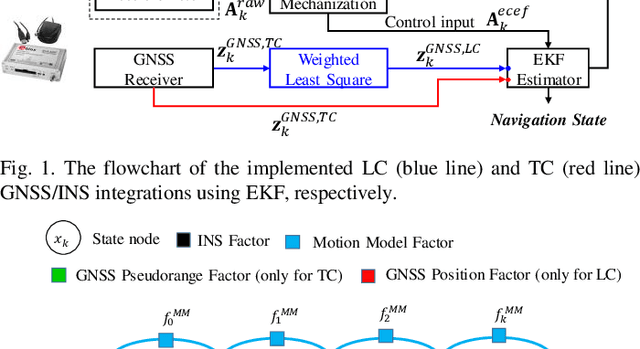
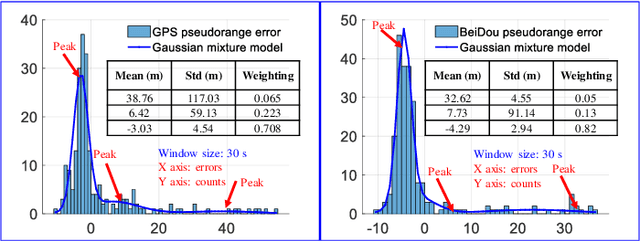
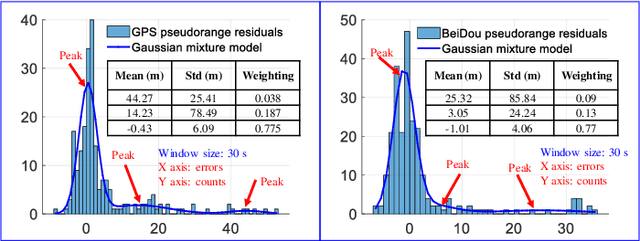
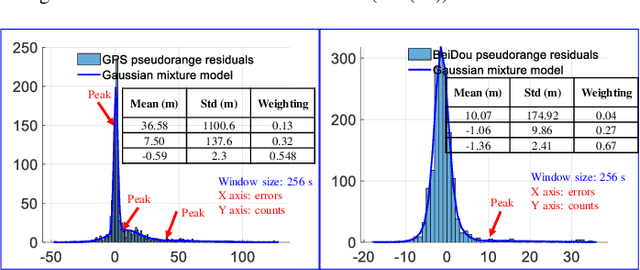
Abstract:The recently proposed factor graph optimization (FGO) is adopted to integrate GNSS/INS attracted lots of attention and improved the performance over the existing EKF-based GNSS/INS integrations. However, a comprehensive comparison of those two GNSS/INS integration schemes in the urban canyon is not available. Moreover, the performance of the FGO-based GNSS/INS integration rely heavily on the size of the window of optimization. Effectively tuning the window size is still an open question. To fill this gap, this paper evaluates both loosely and tightly-coupled integrations using both EKF and FGO via the challenging dataset collected in the urban canyon. The detailed analysis of the results for the advantages of the FGO is also given in this paper by degenerating the FGO-based estimator to an EKF like estimator. More importantly, we analyze the effects of window size against the performance of FGO, by considering both the GNSS pseudorange error distribution and environmental conditions.
Incrementally Learned Mixture Models for GNSS Localization
Apr 30, 2019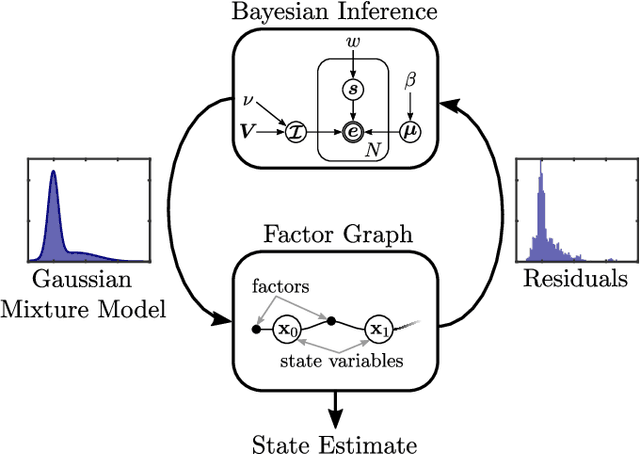
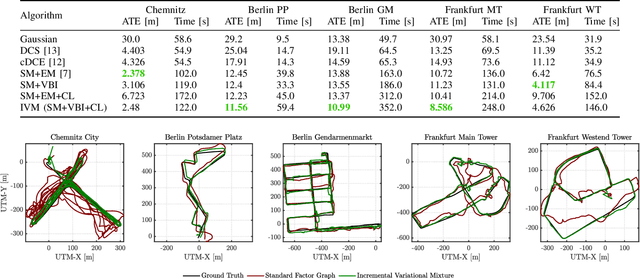

Abstract:GNSS localization is an important part of today's autonomous systems, although it suffers from non-Gaussian errors caused by non-line-of-sight effects. Recent methods are able to mitigate these effects by including the corresponding distributions in the sensor fusion algorithm. However, these approaches require prior knowledge about the sensor's distribution, which is often not available. We introduce a novel sensor fusion algorithm based on variational Bayesian inference, that is able to approximate the true distribution with a Gaussian mixture model and to learn its parametrization online. The proposed Incremental Variational Mixture algorithm automatically adapts the number of mixture components to the complexity of the measurement's error distribution. We compare the proposed algorithm against current state-of-the-art approaches using a collection of open access real world datasets and demonstrate its superior localization accuracy.
Expectation-Maximization for Adaptive Mixture Models in Graph Optimization
Feb 27, 2019
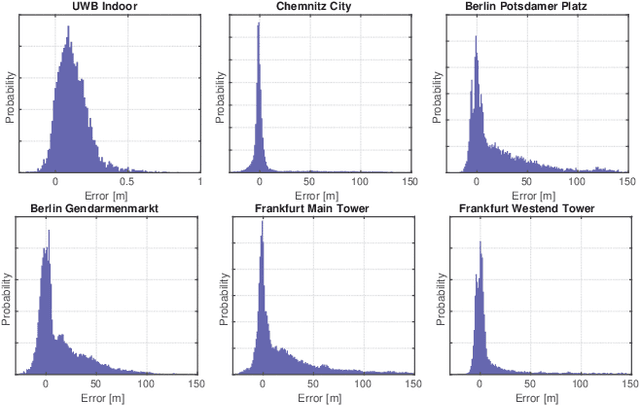

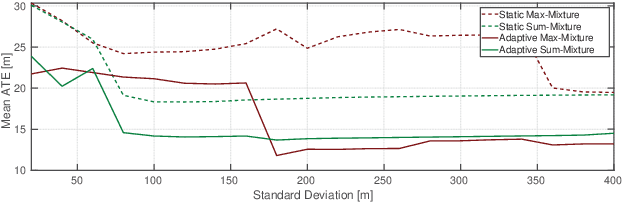
Abstract:Non-Gaussian and multimodal distributions are an important part of many recent robust sensor fusion algorithms. In difference to robust cost functions, they are probabilistically founded and have good convergence properties. Since their robustness depends on a close approximation of the real error distribution, their parametrization is crucial. We propose a novel approach that allows to adapt a multi-modal Gaussian mixture model to the error distribution of a sensor fusion problem. By combining expectation-maximization and non-linear least squares optimization, we are able to provide a computationally efficient solution with well-behaved convergence properties. We demonstrate the performance of these algorithms on several real-world GNSS and indoor localization datasets. The proposed adaptive mixture algorithm outperforms state-of-the-art approaches with static parametrization. Source code and datasets are available under https://mytuc.org/libRSF.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge