A Credible and Robust approach to Ego-Motion Estimation using an Automotive Radar

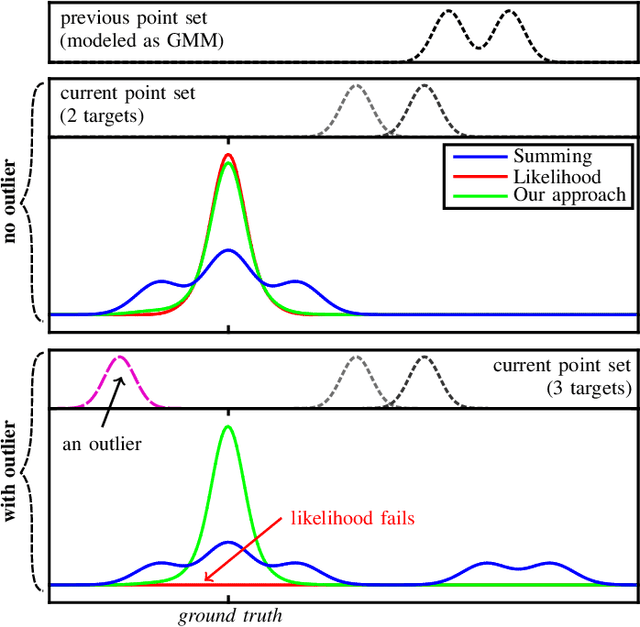
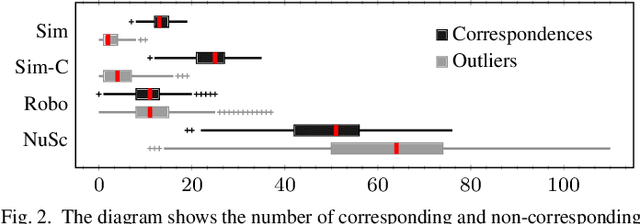
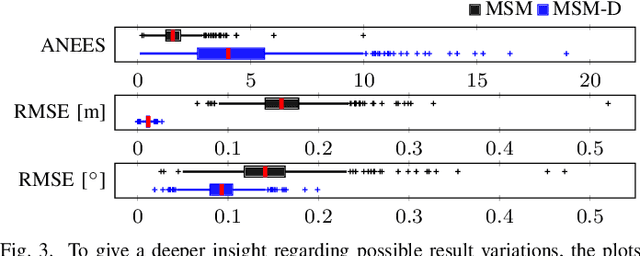
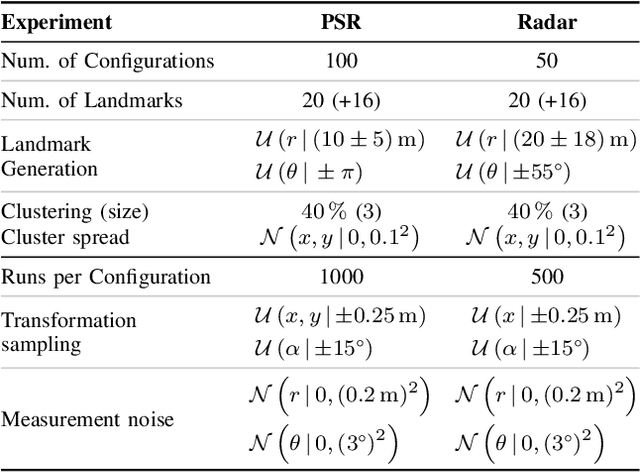
Consistent motion estimation is fundamental for all mobile autonomous systems. While this sounds like an easy task, often, it is not the case because of changing environmental conditions affecting odometry obtained from vision, Lidar, or the wheels themselves. Unsusceptible to challenging lighting and weather conditions, radar sensors are an obvious alternative. Usually, automotive radars return a sparse point cloud, representing the surroundings. Utilizing this information to motion estimation is challenging due to unstable and phantom measurements, which result in a high rate of outliers. We introduce a credible and robust probabilistic approach to estimate the ego-motion based on these challenging radar measurements; intended to be used within a loosely-coupled sensor fusion framework. Compared to existing solutions, evaluated on the popular nuScenes dataset and others, we show that our proposed algorithm is more credible while not depending on explicit correspondence calculation.

Advancing Mixture Models for Least Squares Optimization

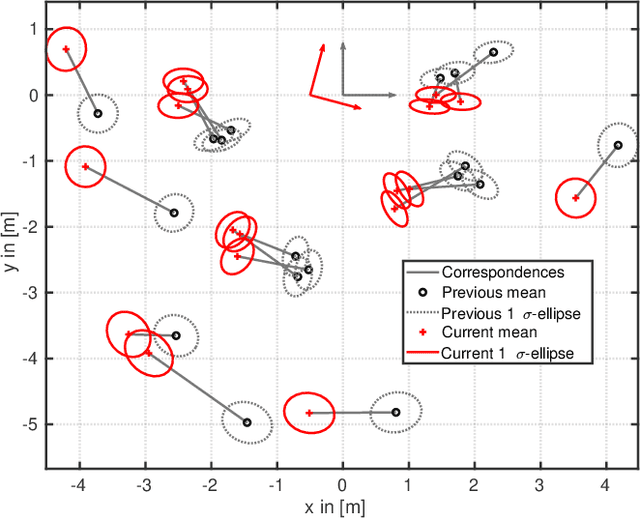
Gaussian mixtures are a powerful and widely used tool to model non-Gaussian estimation problems. They are able to describe measurement errors that follow arbitrary distributions and can represent ambiguity in assignment tasks like point set registration or tracking. However, using them with common least squares solvers is still difficult. Existing approaches are either approximations of the true mixture or prone to convergence issues due to their strong nonlinearity. We propose a novel least squares representation of a Gaussian mixture, which is an exact and almost linear model of the corresponding log-likelihood. Our approach provides an efficient, accurate and flexible model for many probabilistic estimation problems and can be used as cost function for least squares solvers. We demonstrate its superior performance in various Monte Carlo experiments, including different kinds of point set registration. Our implementation is available as open source code for the state-of-the-art solvers Ceres and GTSAM.