Guaranteed Optimal Generative Modeling with Maximum Deviation from the Empirical Distribution

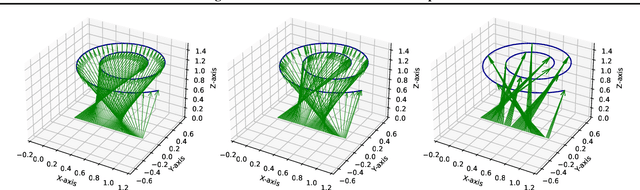
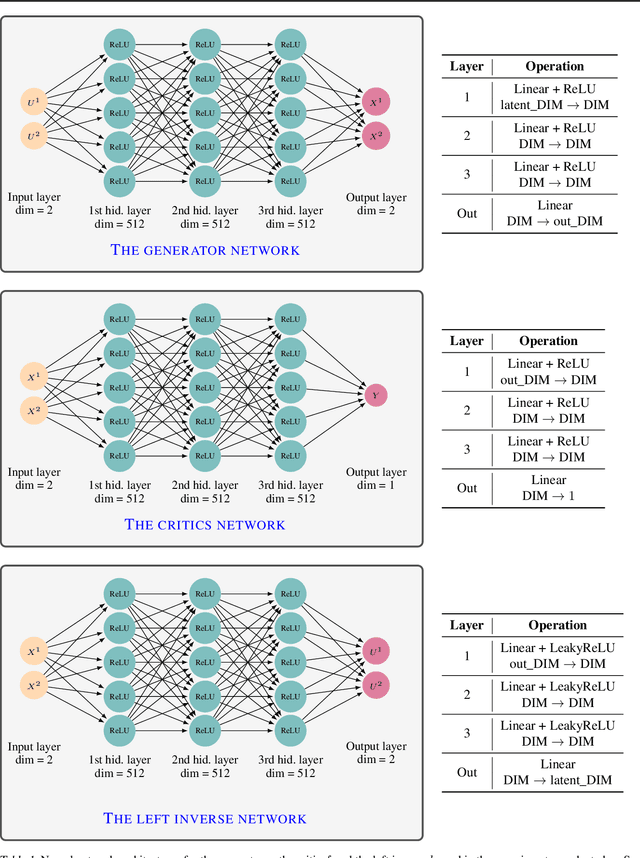
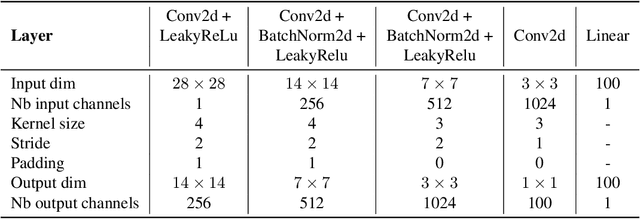
Generative modeling is a widely-used machine learning method with various applications in scientific and industrial fields. Its primary objective is to simulate new examples drawn from an unknown distribution given training data while ensuring diversity and avoiding replication of examples from the training data. This paper presents theoretical insights into training a generative model with two properties: (i) the error of replacing the true data-generating distribution with the trained data-generating distribution should optimally converge to zero as the sample size approaches infinity, and (ii) the trained data-generating distribution should be far enough from any distribution replicating examples in the training data. We provide non-asymptotic results in the form of finite sample risk bounds that quantify these properties and depend on relevant parameters such as sample size, the dimension of the ambient space, and the dimension of the latent space. Our results are applicable to general integral probability metrics used to quantify errors in probability distribution spaces, with the Wasserstein-$1$ distance being the central example. We also include numerical examples to illustrate our theoretical findings.

Matching Map Recovery with an Unknown Number of Outliers

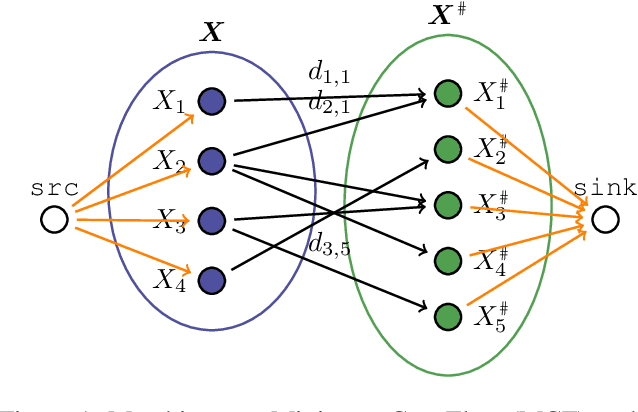
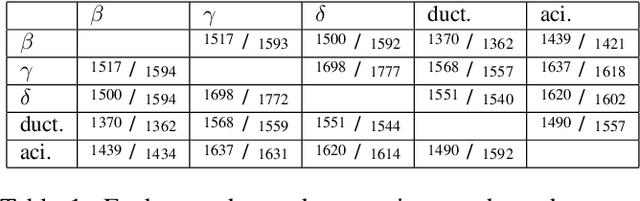
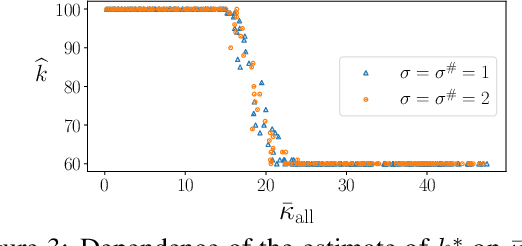
We consider the problem of finding the matching map between two sets of $d$-dimensional noisy feature-vectors. The distinctive feature of our setting is that we do not assume that all the vectors of the first set have their corresponding vector in the second set. If $n$ and $m$ are the sizes of these two sets, we assume that the matching map that should be recovered is defined on a subset of unknown cardinality $k^*\le \min(n,m)$. We show that, in the high-dimensional setting, if the signal-to-noise ratio is larger than $5(d\log(4nm/\alpha))^{1/4}$, then the true matching map can be recovered with probability $1-\alpha$. Interestingly, this threshold does not depend on $k^*$ and is the same as the one obtained in prior work in the case of $k = \min(n,m)$. The procedure for which the aforementioned property is proved is obtained by a data-driven selection among candidate mappings $\{\hat\pi_k:k\in[\min(n,m)]\}$. Each $\hat\pi_k$ minimizes the sum of squares of distances between two sets of size $k$. The resulting optimization problem can be formulated as a minimum-cost flow problem, and thus solved efficiently. Finally, we report the results of numerical experiments on both synthetic and real-world data that illustrate our theoretical results and provide further insight into the properties of the algorithms studied in this work.

Failure Modes of Domain Generalization Algorithms

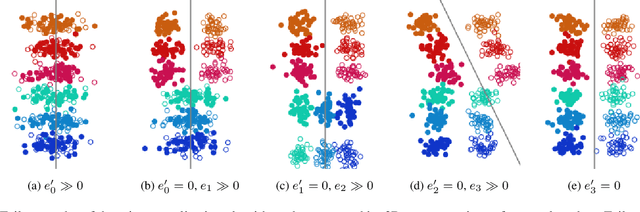
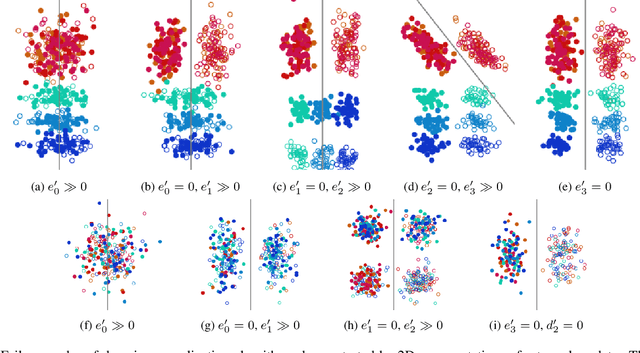
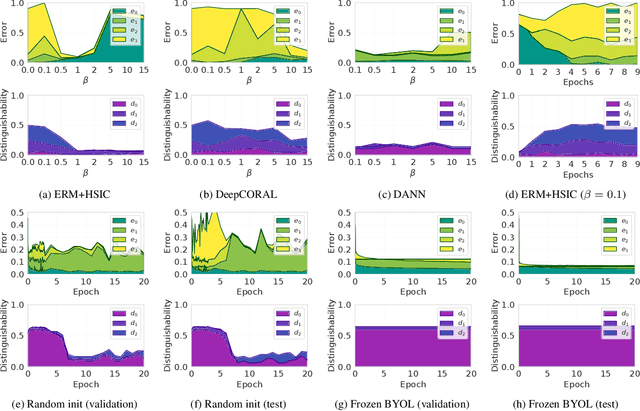
Domain generalization algorithms use training data from multiple domains to learn models that generalize well to unseen domains. While recently proposed benchmarks demonstrate that most of the existing algorithms do not outperform simple baselines, the established evaluation methods fail to expose the impact of various factors that contribute to the poor performance. In this paper we propose an evaluation framework for domain generalization algorithms that allows decomposition of the error into components capturing distinct aspects of generalization. Inspired by the prevalence of algorithms based on the idea of domain-invariant representation learning, we extend the evaluation framework to capture various types of failures in achieving invariance. We show that the largest contributor to the generalization error varies across methods, datasets, regularization strengths and even training lengths. We observe two problems associated with the strategy of learning domain-invariant representations. On Colored MNIST, most domain generalization algorithms fail because they reach domain-invariance only on the training domains. On Camelyon-17, domain-invariance degrades the quality of representations on unseen domains. We hypothesize that focusing instead on tuning the classifier on top of a rich representation can be a promising direction.

Optimal detection of the feature matching map in presence of noise and outliers

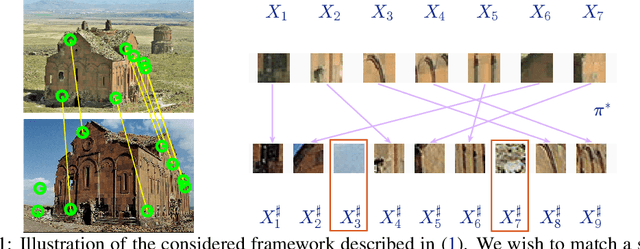
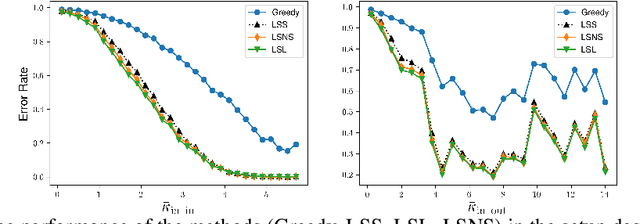
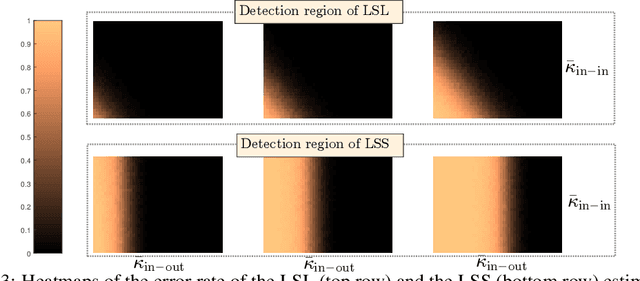
We consider the problem of finding the matching map between two sets of $d$ dimensional vectors from noisy observations, where the second set contains outliers. The matching map is then an injection, which can be consistently estimated only if the vectors of the second set are well separated. The main result shows that, in the high-dimensional setting, a detection region of unknown injection can be characterized by the sets of vectors for which the inlier-inlier distance is of order at least $d^{1/4}$ and the inlier-outlier distance is of order at least $d^{1/2}$. These rates are achieved using the estimated matching minimizing the sum of logarithms of distances between matched pairs of points. We also prove lower bounds establishing optimality of these rates. Finally, we report results of numerical experiments on both synthetic and real world data that illustrate our theoretical results and provide further insight into the properties of the estimators studied in this work.

Robust Classification under Class-Dependent Domain Shift

Investigation of machine learning algorithms robust to changes between the training and test distributions is an active area of research. In this paper we explore a special type of dataset shift which we call class-dependent domain shift. It is characterized by the following features: the input data causally depends on the label, the shift in the data is fully explained by a known variable, the variable which controls the shift can depend on the label, there is no shift in the label distribution. We define a simple optimization problem with an information theoretic constraint and attempt to solve it with neural networks. Experiments on a toy dataset demonstrate the proposed method is able to learn robust classifiers which generalize well to unseen domains.