Arshak Minasyan
Guaranteed Optimal Generative Modeling with Maximum Deviation from the Empirical Distribution
Jul 31, 2023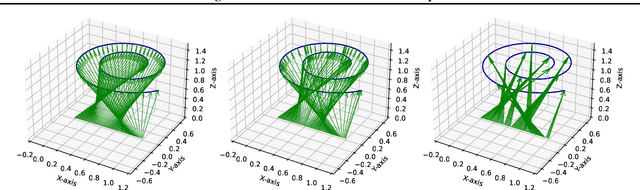
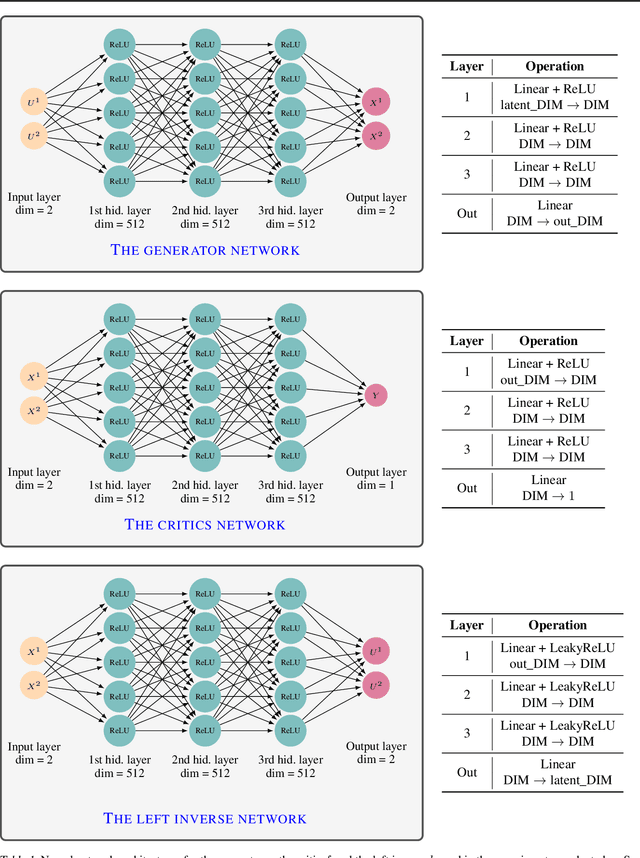

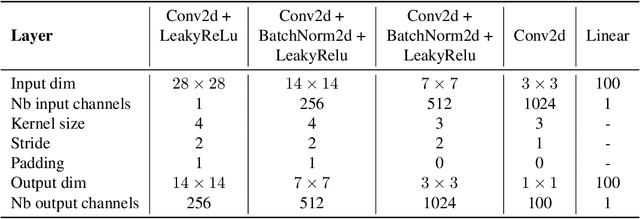
Abstract:Generative modeling is a widely-used machine learning method with various applications in scientific and industrial fields. Its primary objective is to simulate new examples drawn from an unknown distribution given training data while ensuring diversity and avoiding replication of examples from the training data. This paper presents theoretical insights into training a generative model with two properties: (i) the error of replacing the true data-generating distribution with the trained data-generating distribution should optimally converge to zero as the sample size approaches infinity, and (ii) the trained data-generating distribution should be far enough from any distribution replicating examples in the training data. We provide non-asymptotic results in the form of finite sample risk bounds that quantify these properties and depend on relevant parameters such as sample size, the dimension of the ambient space, and the dimension of the latent space. Our results are applicable to general integral probability metrics used to quantify errors in probability distribution spaces, with the Wasserstein-$1$ distance being the central example. We also include numerical examples to illustrate our theoretical findings.
Statistically Optimal Robust Mean and Covariance Estimation for Anisotropic Gaussians
Jan 21, 2023Abstract:Assume that $X_{1}, \ldots, X_{N}$ is an $\varepsilon$-contaminated sample of $N$ independent Gaussian vectors in $\mathbb{R}^d$ with mean $\mu$ and covariance $\Sigma$. In the strong $\varepsilon$-contamination model we assume that the adversary replaced an $\varepsilon$ fraction of vectors in the original Gaussian sample by any other vectors. We show that there is an estimator $\widehat \mu$ of the mean satisfying, with probability at least $1 - \delta$, a bound of the form \[ \|\widehat{\mu} - \mu\|_2 \le c\left(\sqrt{\frac{\operatorname{Tr}(\Sigma)}{N}} + \sqrt{\frac{\|\Sigma\|\log(1/\delta)}{N}} + \varepsilon\sqrt{\|\Sigma\|}\right), \] where $c > 0$ is an absolute constant and $\|\Sigma\|$ denotes the operator norm of $\Sigma$. In the same contaminated Gaussian setup, we construct an estimator $\widehat \Sigma$ of the covariance matrix $\Sigma$ that satisfies, with probability at least $1 - \delta$, \[ \left\|\widehat{\Sigma} - \Sigma\right\| \le c\left(\sqrt{\frac{\|\Sigma\|\operatorname{Tr}(\Sigma)}{N}} + \|\Sigma\|\sqrt{\frac{\log(1/\delta)}{N}} + \varepsilon\|\Sigma\|\right). \] Both results are optimal up to multiplicative constant factors. Despite the recent significant interest in robust statistics, achieving both dimension-free bounds in the canonical Gaussian case remained open. In fact, several previously known results were either dimension-dependent and required $\Sigma$ to be close to identity, or had a sub-optimal dependence on the contamination level $\varepsilon$. As a part of the analysis, we derive sharp concentration inequalities for central order statistics of Gaussian, folded normal, and chi-squared distributions.
Matching Map Recovery with an Unknown Number of Outliers
Oct 24, 2022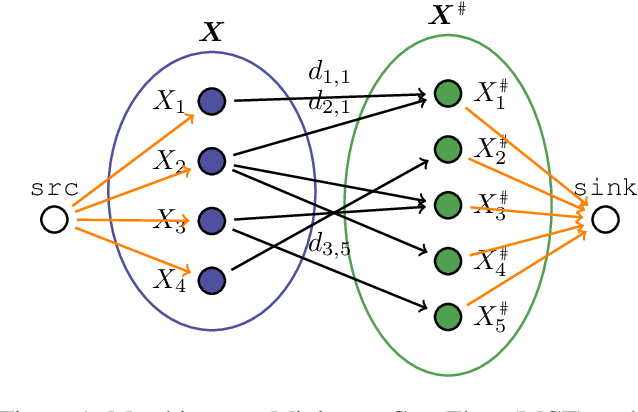
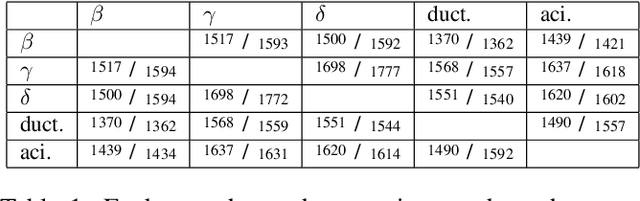

Abstract:We consider the problem of finding the matching map between two sets of $d$-dimensional noisy feature-vectors. The distinctive feature of our setting is that we do not assume that all the vectors of the first set have their corresponding vector in the second set. If $n$ and $m$ are the sizes of these two sets, we assume that the matching map that should be recovered is defined on a subset of unknown cardinality $k^*\le \min(n,m)$. We show that, in the high-dimensional setting, if the signal-to-noise ratio is larger than $5(d\log(4nm/\alpha))^{1/4}$, then the true matching map can be recovered with probability $1-\alpha$. Interestingly, this threshold does not depend on $k^*$ and is the same as the one obtained in prior work in the case of $k = \min(n,m)$. The procedure for which the aforementioned property is proved is obtained by a data-driven selection among candidate mappings $\{\hat\pi_k:k\in[\min(n,m)]\}$. Each $\hat\pi_k$ minimizes the sum of squares of distances between two sets of size $k$. The resulting optimization problem can be formulated as a minimum-cost flow problem, and thus solved efficiently. Finally, we report the results of numerical experiments on both synthetic and real-world data that illustrate our theoretical results and provide further insight into the properties of the algorithms studied in this work.
Nearly minimax robust estimator of the mean vector by iterative spectral dimension reduction
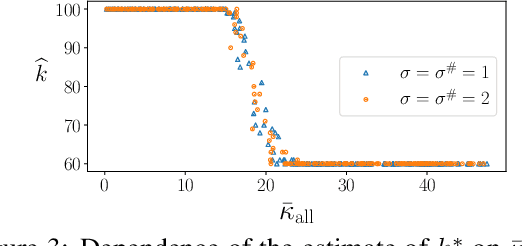
Apr 05, 2022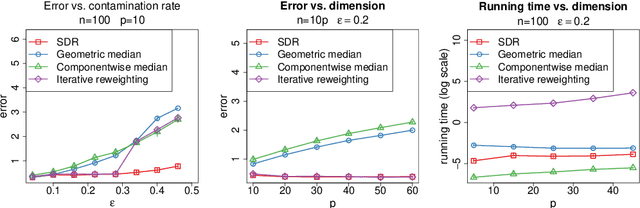
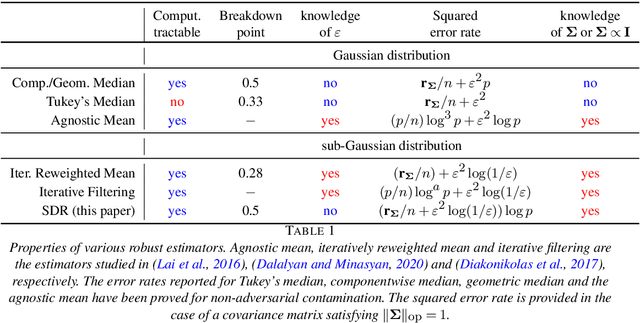
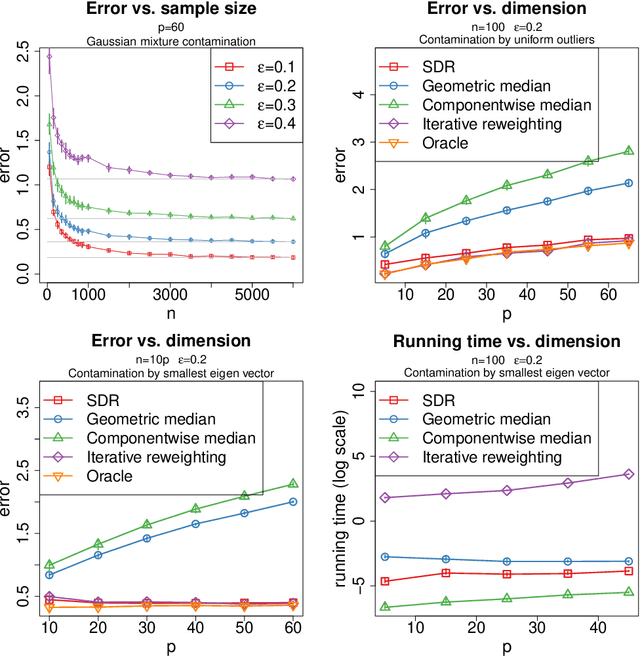
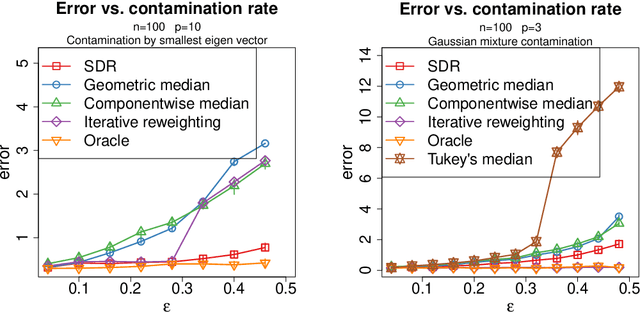
Abstract:We study the problem of robust estimation of the mean vector of a sub-Gaussian distribution. We introduce an estimator based on spectral dimension reduction (SDR) and establish a finite sample upper bound on its error that is minimax-optimal up to a logarithmic factor. Furthermore, we prove that the breakdown point of the SDR estimator is equal to $1/2$, the highest possible value of the breakdown point. In addition, the SDR estimator is equivariant by similarity transforms and has low computational complexity. More precisely, in the case of $n$ vectors of dimension $p$ -- at most $\varepsilon n$ out of which are adversarially corrupted -- the SDR estimator has a squared error of order $\big(\frac{r_\Sigma}{n} + \varepsilon^2\log(1/\varepsilon)\big){\log p}$ and a running time of order $p^3 + n p^2$. Here, $r_\Sigma\le p$ is the effective rank of the covariance matrix of the reference distribution. Another advantage of the SDR estimator is that it does not require knowledge of the contamination rate and does not involve sample splitting. We also investigate extensions of the proposed algorithm and of the obtained results in the case of (partially) unknown covariance matrix.
Optimal detection of the feature matching map in presence of noise and outliers
Jun 13, 2021
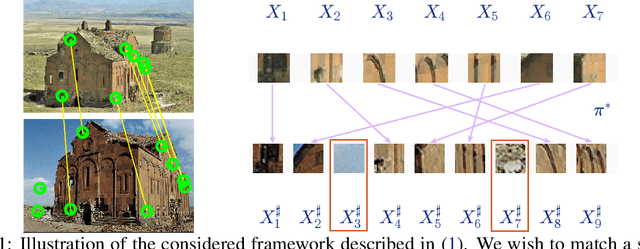
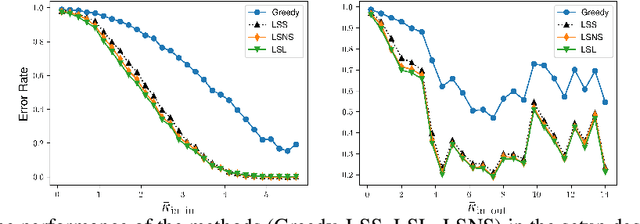
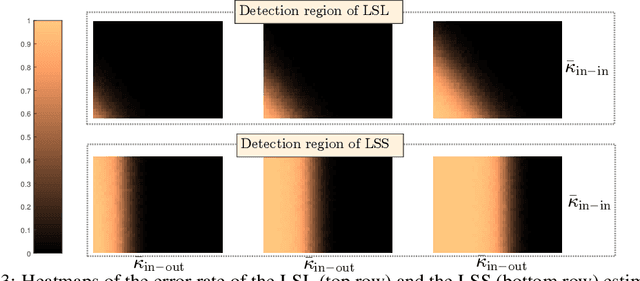
Abstract:We consider the problem of finding the matching map between two sets of $d$ dimensional vectors from noisy observations, where the second set contains outliers. The matching map is then an injection, which can be consistently estimated only if the vectors of the second set are well separated. The main result shows that, in the high-dimensional setting, a detection region of unknown injection can be characterized by the sets of vectors for which the inlier-inlier distance is of order at least $d^{1/4}$ and the inlier-outlier distance is of order at least $d^{1/2}$. These rates are achieved using the estimated matching minimizing the sum of logarithms of distances between matched pairs of points. We also prove lower bounds establishing optimality of these rates. Finally, we report results of numerical experiments on both synthetic and real world data that illustrate our theoretical results and provide further insight into the properties of the estimators studied in this work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge