Nearly minimax robust estimator of the mean vector by iterative spectral dimension reduction

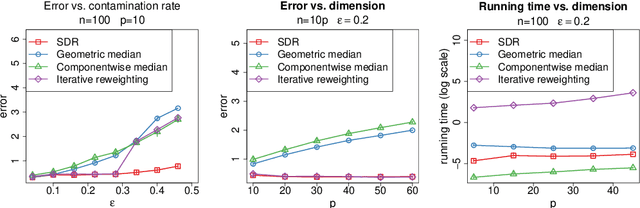
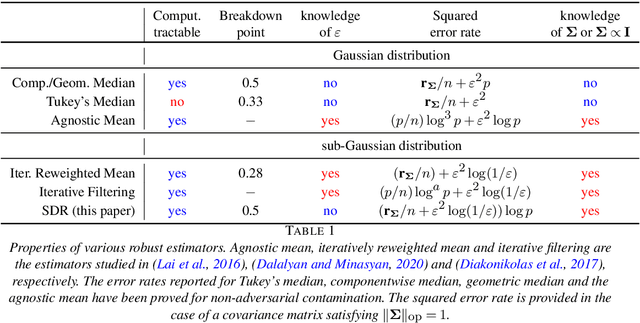
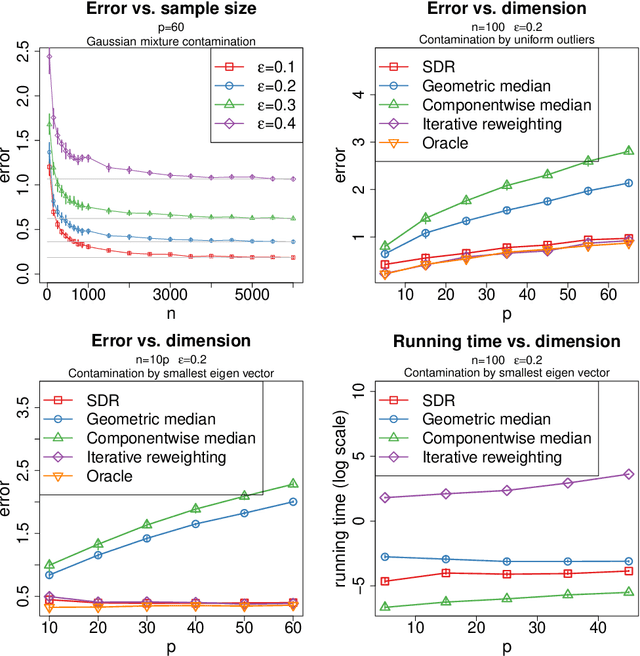
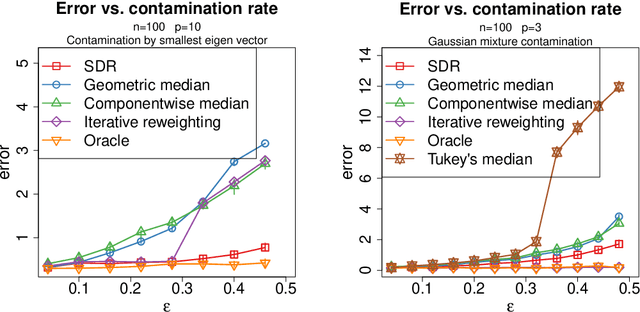
We study the problem of robust estimation of the mean vector of a sub-Gaussian distribution. We introduce an estimator based on spectral dimension reduction (SDR) and establish a finite sample upper bound on its error that is minimax-optimal up to a logarithmic factor. Furthermore, we prove that the breakdown point of the SDR estimator is equal to $1/2$, the highest possible value of the breakdown point. In addition, the SDR estimator is equivariant by similarity transforms and has low computational complexity. More precisely, in the case of $n$ vectors of dimension $p$ -- at most $\varepsilon n$ out of which are adversarially corrupted -- the SDR estimator has a squared error of order $\big(\frac{r_\Sigma}{n} + \varepsilon^2\log(1/\varepsilon)\big){\log p}$ and a running time of order $p^3 + n p^2$. Here, $r_\Sigma\le p$ is the effective rank of the covariance matrix of the reference distribution. Another advantage of the SDR estimator is that it does not require knowledge of the contamination rate and does not involve sample splitting. We also investigate extensions of the proposed algorithm and of the obtained results in the case of (partially) unknown covariance matrix.

Minimax rates in outlier-robust estimation of discrete models

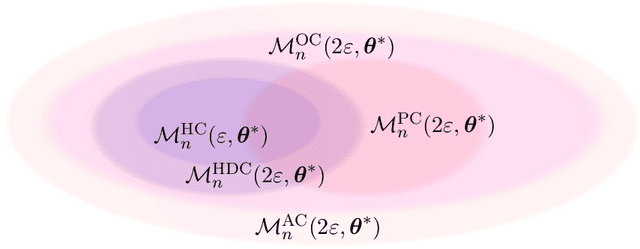
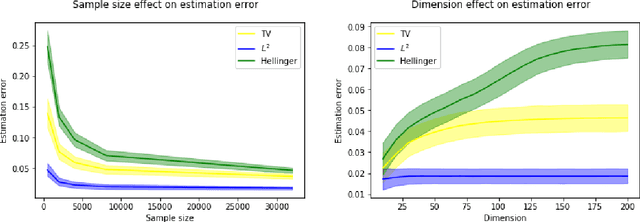
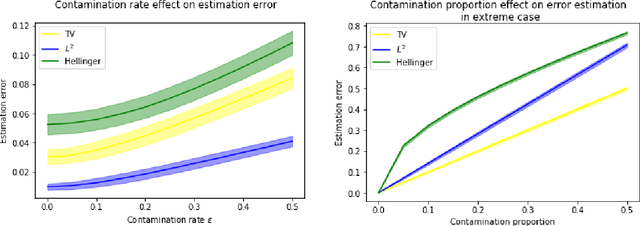
We consider the problem of estimating the probability distribution of a discrete random variable in the setting where the observations are corrupted by outliers. Assuming that the discrete variable takes k values, the unknown parameter p is a k-dimensional vector belonging to the probability simplex. We first describe various settings of contamination and discuss the relation between these settings. We then establish minimax rates when the quality of estimation is measured by the total-variation distance, the Hellinger distance, or the L2-distance between two probability measures. Our analysis reveals that the minimax rates associated to these three distances are all different, but they are all attained by the maximum likelihood estimator. Note that the latter is efficiently computable even when the dimension is large. Some numerical experiments illustrating our theoretical findings are reported.