OCTAL: Graph Representation Learning for LTL Model Checking

Model Checking is widely applied in verifying the correctness of complex and concurrent systems against a specification. Pure symbolic approaches while popular, still suffer from the state space explosion problem that makes them impractical for large scale systems and/or specifications. In this paper, we propose to use graph representation learning (GRL) for solving linear temporal logic (LTL) model checking, where the system and the specification are expressed by a B\"uchi automaton and an LTL formula respectively. A novel GRL-based framework OCTAL, is designed to learn the representation of the graph-structured system and specification, which reduces the model checking problem to binary classification in the latent space. The empirical experiments show that OCTAL achieves comparable accuracy against canonical SOTA model checkers on three different datasets, with up to $5\times$ overall speedup and above $63\times$ for satisfiability checking alone.

Graph Neural Reasoning for 2-Quantified Boolean Formula Solvers

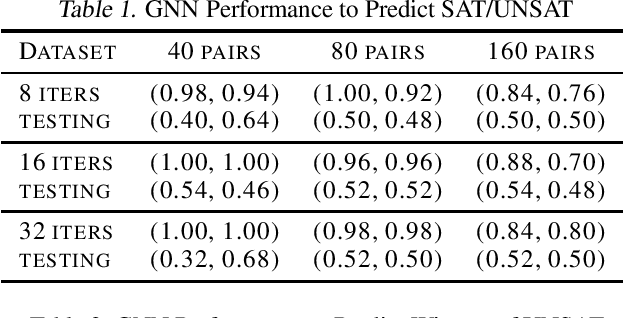
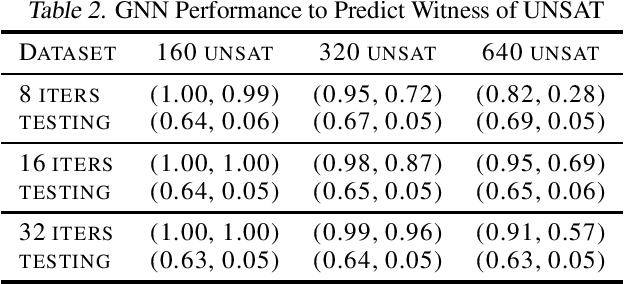
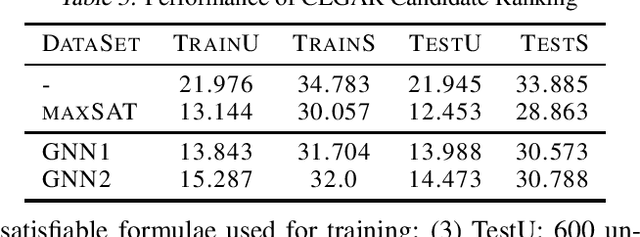
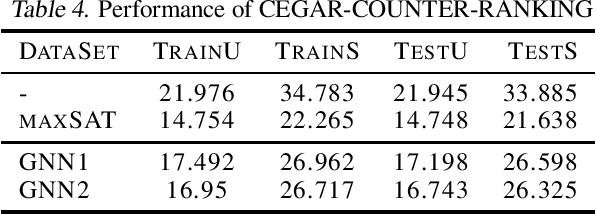
In this paper, we investigate the feasibility of learning GNN (Graph Neural Network) based solvers and GNN-based heuristics for specified QBF (Quantified Boolean Formula) problems. We design and evaluate several GNN architectures for 2QBF formulae, and conjecture that GNN has limitations in learning 2QBF solvers. Then we show how to learn a heuristic CEGAR 2QBF solver. We further explore generalizing GNN-based heuristics to larger unseen instances, and uncover some interesting challenges. In summary, this paper provides a comprehensive surveying view of applying GNN-embeddings to specified QBF solvers, and aims to offer guidance in applying ML to more complicated symbolic reasoning problems.

AutoGraph: Imperative-style Coding with Graph-based Performance

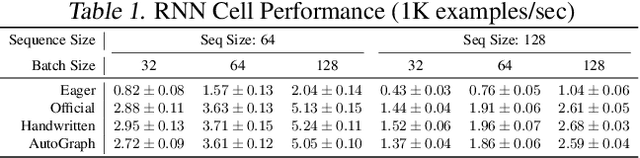
There is a perceived trade-off between machine learning code that is easy to write, and machine learning code that is scalable or fast to execute. In machine learning, imperative style libraries like Autograd and PyTorch are easy to write, but suffer from high interpretive overhead and are not easily deployable in production or mobile settings. Graph-based libraries like TensorFlow and Theano benefit from whole-program optimization and can be deployed broadly, but make expressing complex models more cumbersome. We describe how the use of staged programming in Python, via source code transformation, offers a midpoint between these two library design patterns, capturing the benefits of both. A key insight is to delay all type-dependent decisions until runtime, via dynamic dispatch. We instantiate these principles in AutoGraph, a software system that improves the programming experience of the TensorFlow library, and demonstrate usability improvements with no loss in performance compared to native TensorFlow graphs. We also show that our system is backend agnostic, and demonstrate targeting an alternate IR with characteristics not found in TensorFlow graphs.

Demystifying Differentiable Programming: Shift/Reset the Penultimate Backpropagator

Deep learning has seen tremendous success over the past decade in computer vision, machine translation, and gameplay. This success rests in crucial ways on gradient-descent optimization and the ability to learn parameters of a neural network by backpropagating observed errors. However, neural network architectures are growing increasingly sophisticated and diverse, which motivates an emerging quest for even more general forms of differentiable programming, where arbitrary parameterized computations can be trained by gradient descent. In this paper, we take a fresh look at automatic differentiation (AD) techniques, and especially aim to demystify the reverse-mode form of AD that generalizes backpropagation in neural networks. We uncover a tight connection between reverse-mode AD and delimited continuations, which permits implementing reverse-mode AD purely via operator overloading and without any auxiliary data structures. We further show how this formulation of AD can be fruitfully combined with multi-stage programming (staging), leading to a highly efficient implementation that combines the performance benefits of deep learning frameworks based on explicit reified computation graphs (e.g., TensorFlow) with the expressiveness of pure library approaches (e.g., PyTorch).

From Gameplay to Symbolic Reasoning: Learning SAT Solver Heuristics in the Style of Alpha(Go) Zero

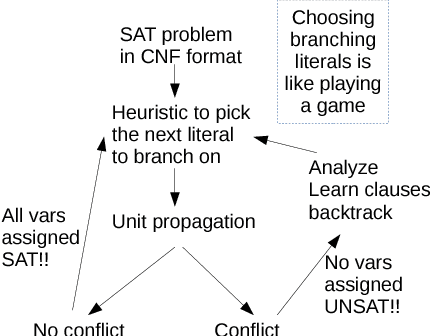
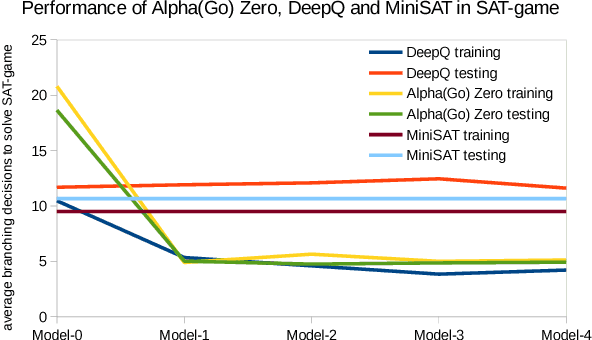
Despite the recent successes of deep neural networks in various fields such as image and speech recognition, natural language processing, and reinforcement learning, we still face big challenges in bringing the power of numeric optimization to symbolic reasoning. Researchers have proposed different avenues such as neural machine translation for proof synthesis, vectorization of symbols and expressions for representing symbolic patterns, and coupling of neural back-ends for dimensionality reduction with symbolic front-ends for decision making. However, these initial explorations are still only point solutions, and bear other shortcomings such as lack of correctness guarantees. In this paper, we present our approach of casting symbolic reasoning as games, and directly harnessing the power of deep reinforcement learning in the style of Alpha(Go) Zero on symbolic problems. Using the Boolean Satisfiability (SAT) problem as showcase, we demonstrate the feasibility of our method, and the advantages of modularity, efficiency, and correctness guarantees.