3D Geometry-aware Deformable Gaussian Splatting for Dynamic View Synthesis

In this paper, we propose a 3D geometry-aware deformable Gaussian Splatting method for dynamic view synthesis. Existing neural radiance fields (NeRF) based solutions learn the deformation in an implicit manner, which cannot incorporate 3D scene geometry. Therefore, the learned deformation is not necessarily geometrically coherent, which results in unsatisfactory dynamic view synthesis and 3D dynamic reconstruction. Recently, 3D Gaussian Splatting provides a new representation of the 3D scene, building upon which the 3D geometry could be exploited in learning the complex 3D deformation. Specifically, the scenes are represented as a collection of 3D Gaussian, where each 3D Gaussian is optimized to move and rotate over time to model the deformation. To enforce the 3D scene geometry constraint during deformation, we explicitly extract 3D geometry features and integrate them in learning the 3D deformation. In this way, our solution achieves 3D geometry-aware deformation modeling, which enables improved dynamic view synthesis and 3D dynamic reconstruction. Extensive experimental results on both synthetic and real datasets prove the superiority of our solution, which achieves new state-of-the-art performance. The project is available at https://npucvr.github.io/GaGS/

Model-free Optimization and Experimental Validation of RIS-assisted Wireless Communications under Rich Multipath Fading

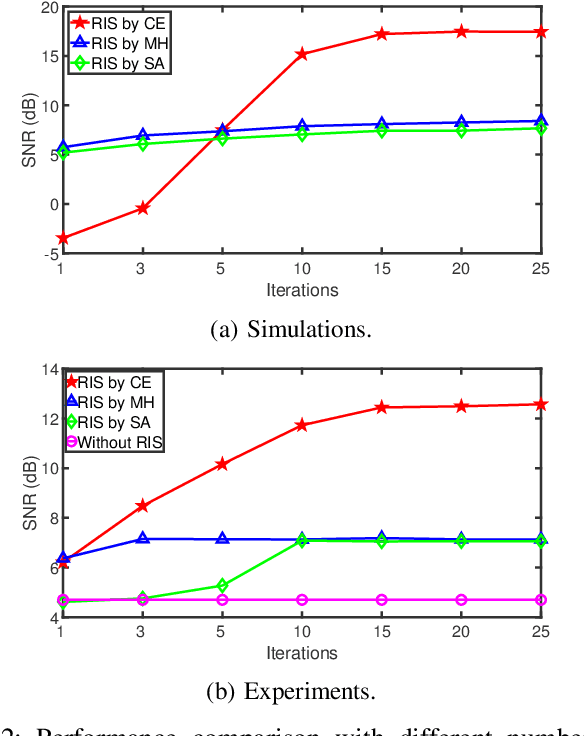
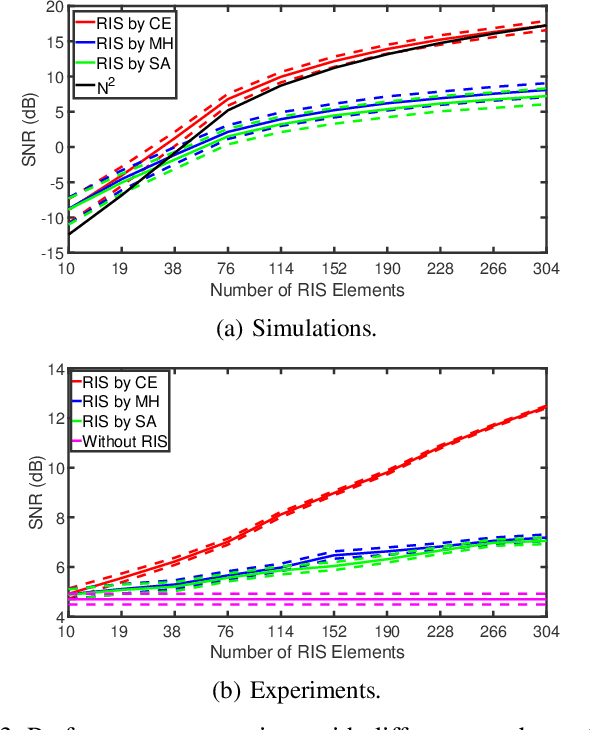
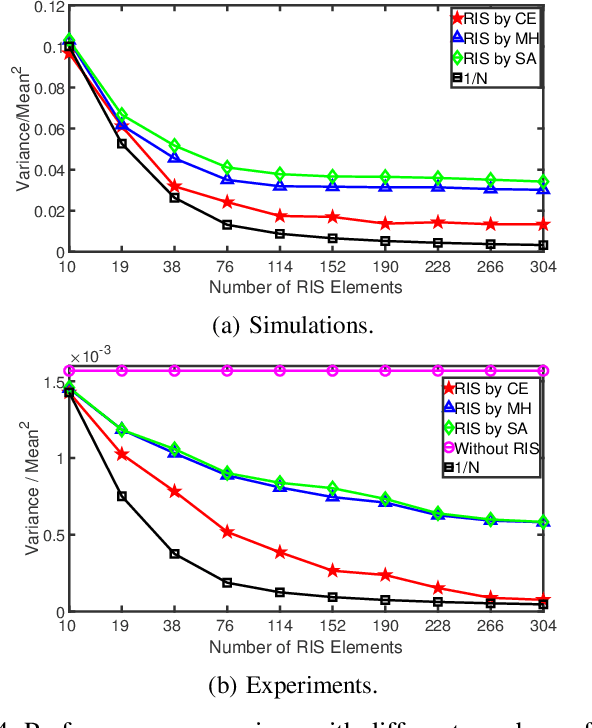
Reconfigurable intelligent surface (RIS) devices have emerged as an effective way to control the propagation channels for enhancing the end users' performance. However, RIS optimization involves configuring the radio frequency (RF) response of a large number of radiating elements, which is challenging in real-world applications due to high computational complexity. In this paper, a model-free cross-entropy (CE) algorithm is proposed to optimize the binary RIS configuration for improving the signal-to-noise ratio (SNR) at the receiver. One key advantage of the proposed method is that it only needs system performance parameters, e.g., the received SNR, without the need for channel models or channel estimation. Both simulations and experiments are conducted to evaluate the performance of the proposed CE algorithm. The results demonstrate that the CE algorithm outperforms benchmark algorithms, and shows stronger channel hardening with increasing numbers of RIS elements.

A Doubly Optimistic Strategy for Safe Linear Bandits

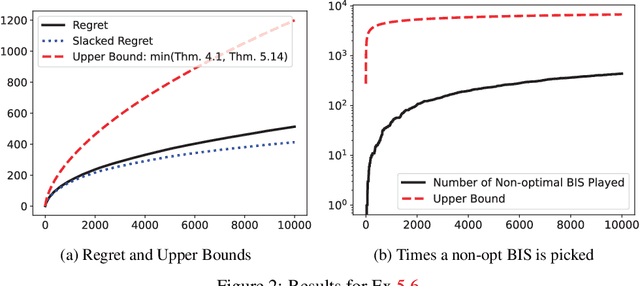
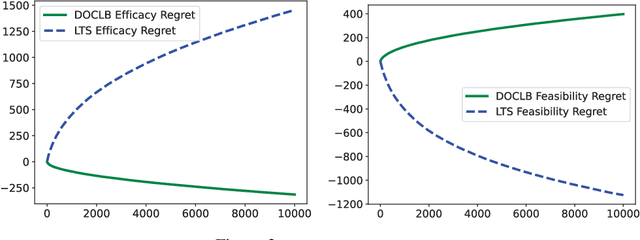
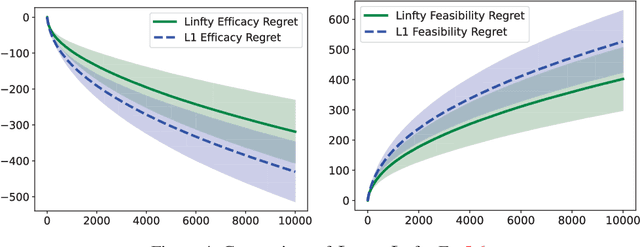
We propose a \underline{d}oubly \underline{o}ptimistic strategy for the \underline{s}afe-\underline{l}inear-\underline{b}andit problem, DOSLB. The safe linear bandit problem is to optimise an unknown linear reward whilst satisfying unknown round-wise safety constraints on actions, using stochastic bandit feedback of reward and safety-risks of actions. In contrast to prior work on aggregated resource constraints, our formulation explicitly demands control on roundwise safety risks. Unlike existing optimistic-pessimistic paradigms for safe bandits, DOSLB exercises supreme optimism, using optimistic estimates of reward and safety scores to select actions. Yet, and surprisingly, we show that DOSLB rarely takes risky actions, and obtains $\tilde{O}(d \sqrt{T})$ regret, where our notion of regret accounts for both inefficiency and lack of safety of actions. Specialising to polytopal domains, we first notably show that the $\sqrt{T}$-regret bound cannot be improved even with large gaps, and then identify a slackened notion of regret for which we show tight instance-dependent $O(\log^2 T)$ bounds. We further argue that in such domains, the number of times an overly risky action is played is also bounded as $O(\log^2T)$.

Strategies for Safe Multi-Armed Bandits with Logarithmic Regret and Risk

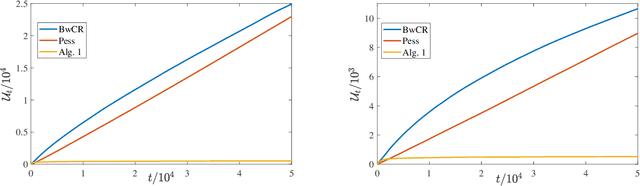
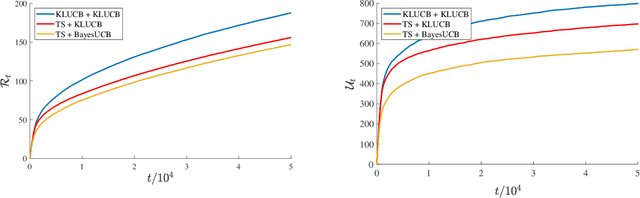
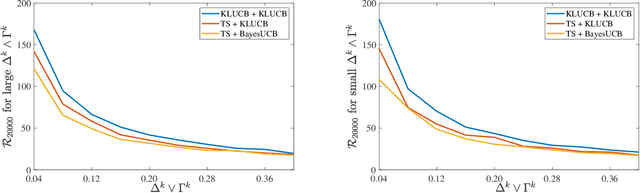
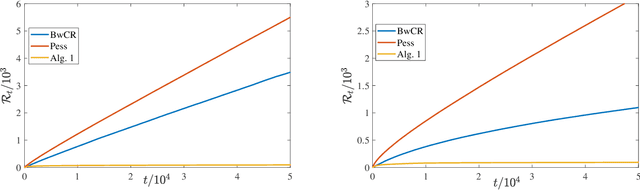
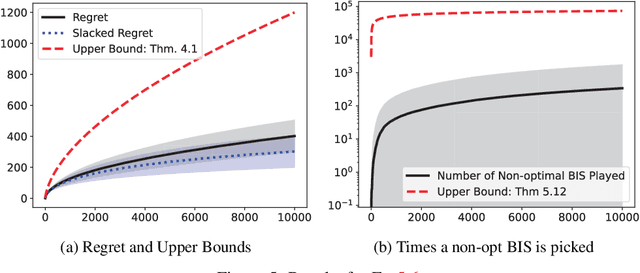
We investigate a natural but surprisingly unstudied approach to the multi-armed bandit problem under safety risk constraints. Each arm is associated with an unknown law on safety risks and rewards, and the learner's goal is to maximise reward whilst not playing unsafe arms, as determined by a given threshold on the mean risk. We formulate a pseudo-regret for this setting that enforces this safety constraint in a per-round way by softly penalising any violation, regardless of the gain in reward due to the same. This has practical relevance to scenarios such as clinical trials, where one must maintain safety for each round rather than in an aggregated sense. We describe doubly optimistic strategies for this scenario, which maintain optimistic indices for both safety risk and reward. We show that schema based on both frequentist and Bayesian indices satisfy tight gap-dependent logarithmic regret bounds, and further that these play unsafe arms only logarithmically many times in total. This theoretical analysis is complemented by simulation studies demonstrating the effectiveness of the proposed schema, and probing the domains in which their use is appropriate.