MeLIME: Meaningful Local Explanation for Machine Learning Models

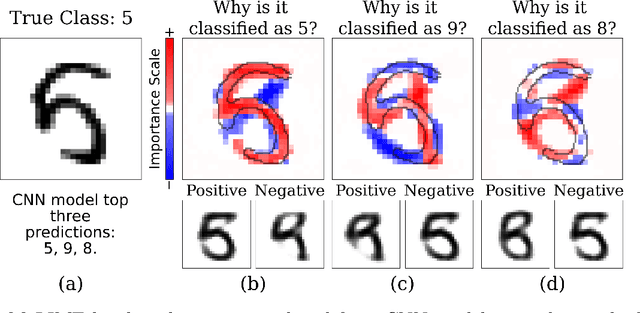
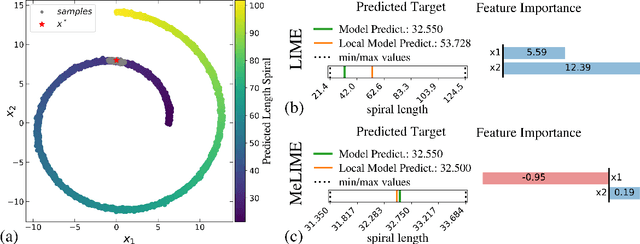
Most state-of-the-art machine learning algorithms induce black-box models, preventing their application in many sensitive domains. Hence, many methodologies for explaining machine learning models have been proposed to address this problem. In this work, we introduce strategies to improve local explanations taking into account the distribution of the data used to train the black-box models. We show that our approach, MeLIME, produces more meaningful explanations compared to other techniques over different ML models, operating on various types of data. MeLIME generalizes the LIME method, allowing more flexible perturbation sampling and the use of different local interpretable models. Additionally, we introduce modifications to standard training algorithms of local interpretable models fostering more robust explanations, even allowing the production of counterfactual examples. To show the strengths of the proposed approach, we include experiments on tabular data, images, and text; all showing improved explanations. In particular, MeLIME generated more meaningful explanations on the MNIST dataset than methods such as GuidedBackprop, SmoothGrad, and Layer-wise Relevance Propagation. MeLIME is available on https://github.com/tiagobotari/melime.

NLS: an accurate and yet easy-to-interpret regression method

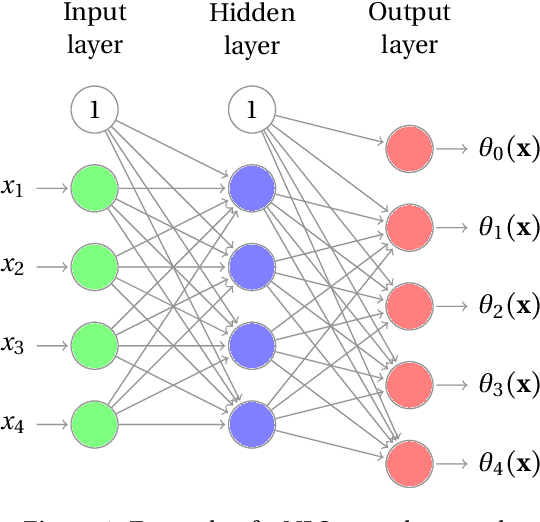
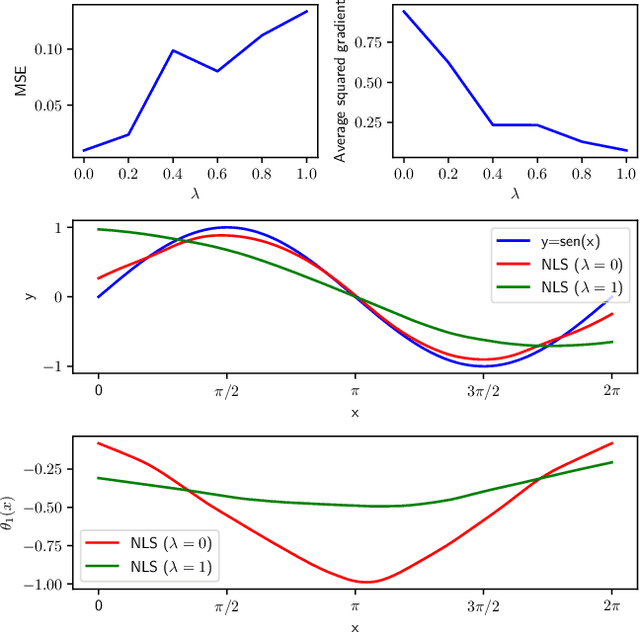
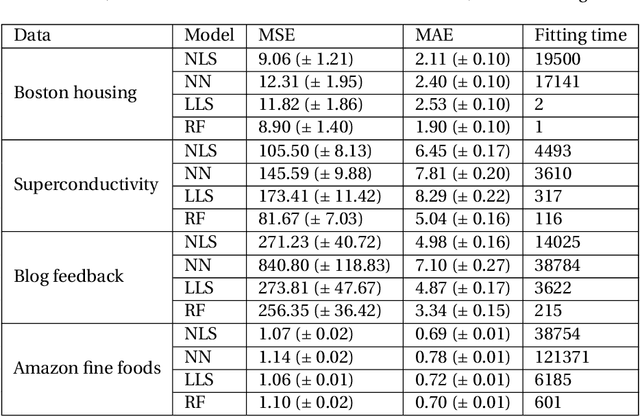
An important feature of successful supervised machine learning applications is to be able to explain the predictions given by the regression or classification model being used. However, most state-of-the-art models that have good predictive power lead to predictions that are hard to interpret. Thus, several model-agnostic interpreters have been developed recently as a way of explaining black-box classifiers. In practice, using these methods is a slow process because a novel fitting is required for each new testing instance, and several non-trivial choices must be made. We develop NLS (neural local smoother), a method that is complex enough to give good predictions, and yet gives solutions that are easy to be interpreted without the need of using a separate interpreter. The key idea is to use a neural network that imposes a local linear shape to the output layer. We show that NLS leads to predictive power that is comparable to state-of-the-art machine learning models, and yet is easier to interpret.

Local Interpretation Methods to Machine Learning Using the Domain of the Feature Space

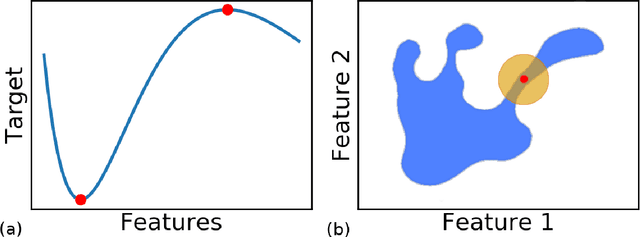
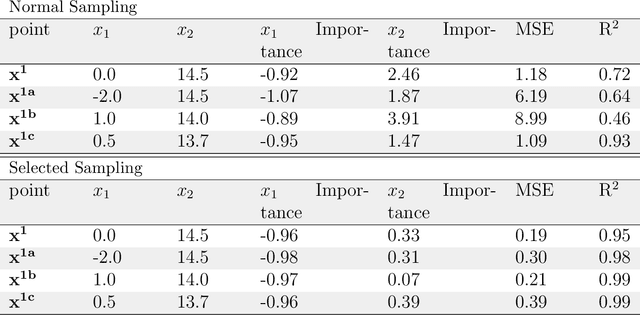
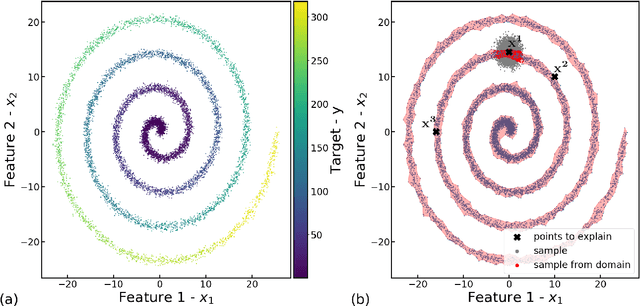
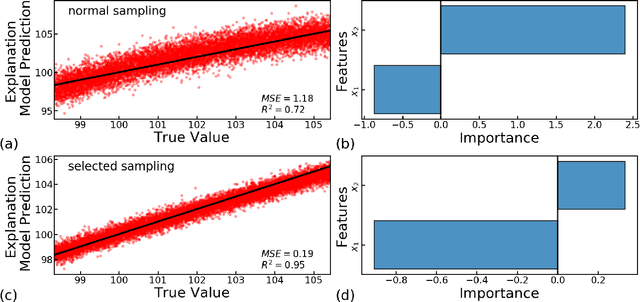
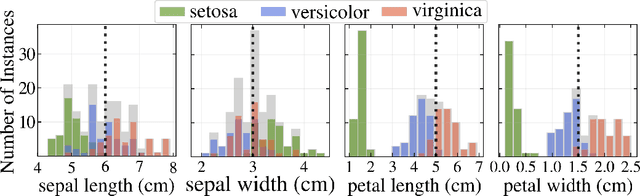
As machine learning becomes an important part of many real world applications affecting human lives, new requirements, besides high predictive accuracy, become important. One important requirement is transparency, which has been associated with model interpretability. Many machine learning algorithms induce models difficult to interpret, named black box. Moreover, people have difficulty to trust models that cannot be explained. In particular for machine learning, many groups are investigating new methods able to explain black box models. These methods usually look inside the black models to explain their inner work. By doing so, they allow the interpretation of the decision making process used by black box models. Among the recently proposed model interpretation methods, there is a group, named local estimators, which are designed to explain how the label of particular instance is predicted. For such, they induce interpretable models on the neighborhood of the instance to be explained. Local estimators have been successfully used to explain specific predictions. Although they provide some degree of model interpretability, it is still not clear what is the best way to implement and apply them. Open questions include: how to best define the neighborhood of an instance? How to control the trade-off between the accuracy of the interpretation method and its interpretability? How to make the obtained solution robust to small variations on the instance to be explained? To answer to these questions, we propose and investigate two strategies: (i) using data instance properties to provide improved explanations, and (ii) making sure that the neighborhood of an instance is properly defined by taking the geometry of the domain of the feature space into account. We evaluate these strategies in a regression task and present experimental results that show that they can improve local explanations.