NLS: an accurate and yet easy-to-interpret regression method

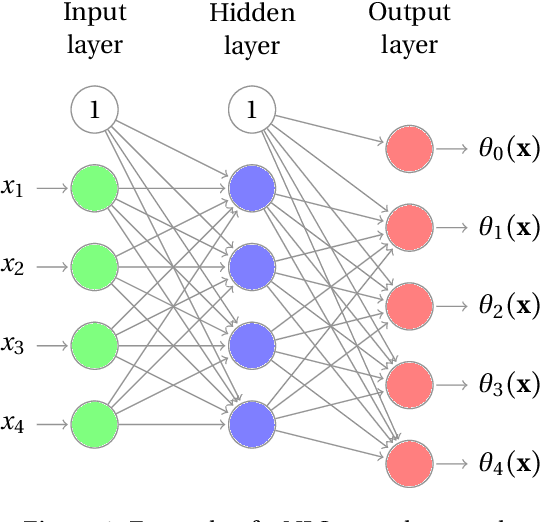
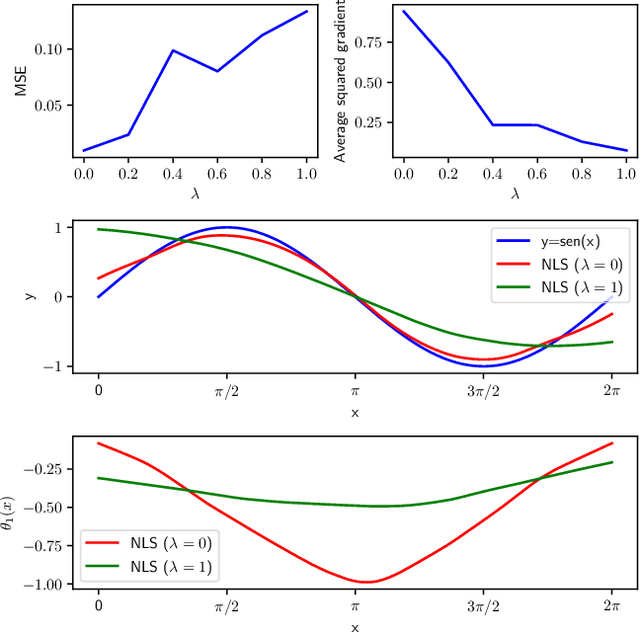
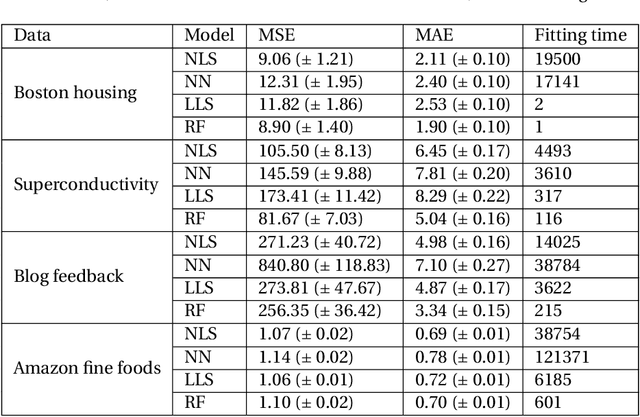
An important feature of successful supervised machine learning applications is to be able to explain the predictions given by the regression or classification model being used. However, most state-of-the-art models that have good predictive power lead to predictions that are hard to interpret. Thus, several model-agnostic interpreters have been developed recently as a way of explaining black-box classifiers. In practice, using these methods is a slow process because a novel fitting is required for each new testing instance, and several non-trivial choices must be made. We develop NLS (neural local smoother), a method that is complex enough to give good predictions, and yet gives solutions that are easy to be interpreted without the need of using a separate interpreter. The key idea is to use a neural network that imposes a local linear shape to the output layer. We show that NLS leads to predictive power that is comparable to state-of-the-art machine learning models, and yet is easier to interpret.

Distance Assessment and Hypothesis Testing of High-Dimensional Samples using Variational Autoencoders

Given two distinct datasets, an important question is if they have arisen from the the same data generating function or alternatively how their data generating functions diverge from one another. In this paper, we introduce an approach for measuring the distance between two datasets with high dimensionality using variational autoencoders. This approach is augmented by a permutation hypothesis test in order to check the hypothesis that the data generating distributions are the same within a significance level. We evaluate both the distance measurement and hypothesis testing approaches on generated and on public datasets. According to the results the proposed approach can be used for data exploration (e.g. by quantifying the discrepancy/separability between categories of images), which can be particularly useful in the early phases of the pipeline of most machine learning projects.

Conditional independence testing: a predictive perspective

Conditional independence testing is a key problem required by many machine learning and statistics tools. In particular, it is one way of evaluating the usefulness of some features on a supervised prediction problem. We propose a novel conditional independence test in a predictive setting, and show that it achieves better power than competing approaches in several settings. Our approach consists in deriving a p-value using a permutation test where the predictive power using the unpermuted dataset is compared with the predictive power of using dataset where the feature(s) of interest are permuted. We conclude that the method achives sensible results on simulated and real datasets.

The NN-Stacking: Feature weighted linear stacking through neural networks

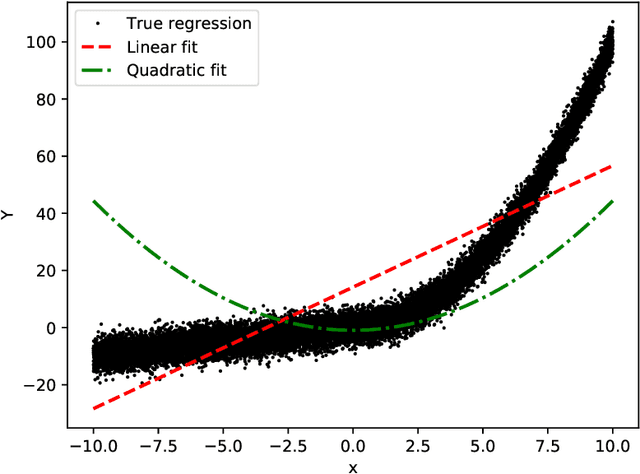
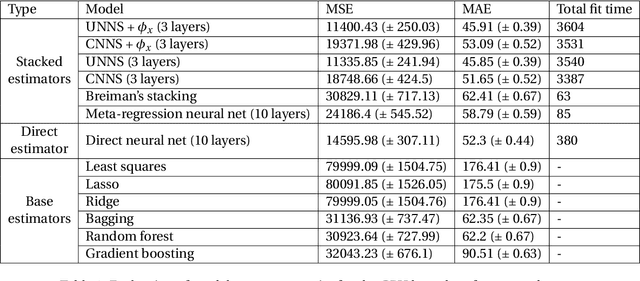
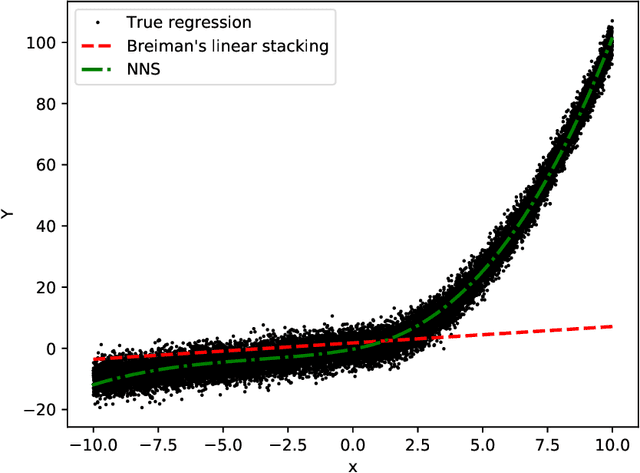
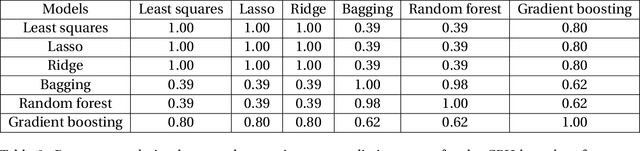
Stacking methods improve the prediction performance of regression models. A simple way to stack base regressions estimators is by combining them linearly, as done by \citet{breiman1996stacked}. Even though this approach is useful from an interpretative perspective, it often does not lead to high predictive power. We propose the NN-Stacking method (NNS), which generalizes Breiman's method by allowing the linear parameters to vary with input features. This improvement enables NNS to take advantage of the fact that distinct base models often perform better at different regions of the feature space. Our method uses neural networks to estimate the stacking coefficients. We show that while our approach keeps the interpretative features of Breiman's method at a local level, it leads to better predictive power, especially in datasets with large sample sizes.