The NN-Stacking: Feature weighted linear stacking through neural networks
Paper and Code
Jun 24, 2019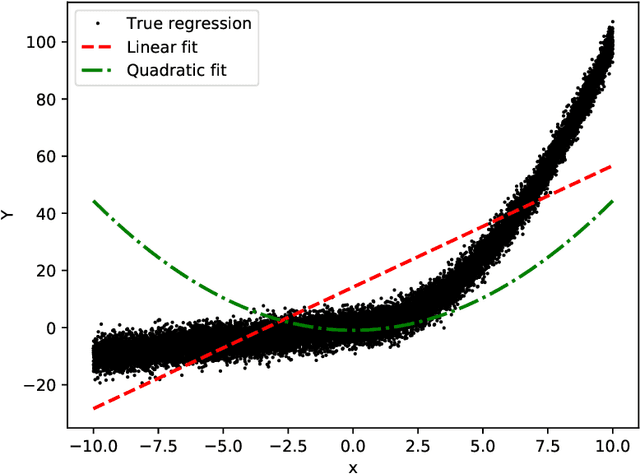
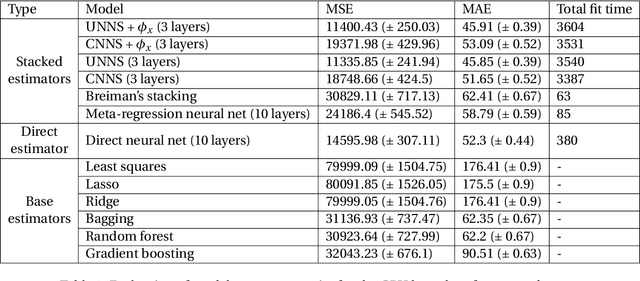
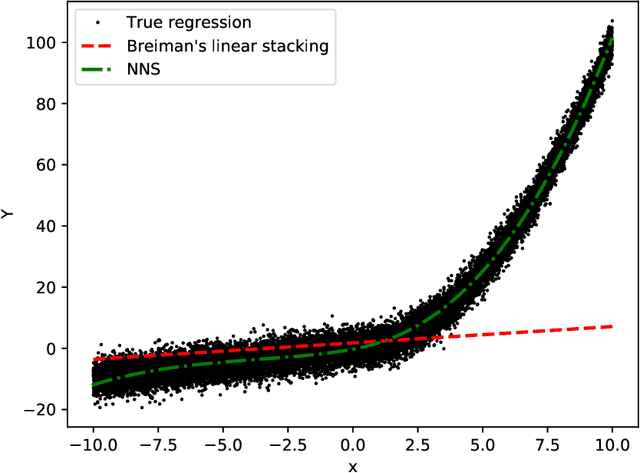
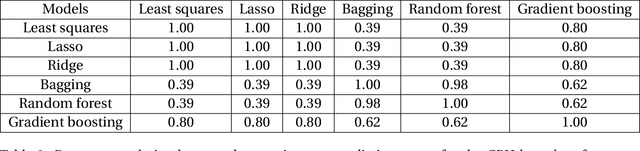
Stacking methods improve the prediction performance of regression models. A simple way to stack base regressions estimators is by combining them linearly, as done by \citet{breiman1996stacked}. Even though this approach is useful from an interpretative perspective, it often does not lead to high predictive power. We propose the NN-Stacking method (NNS), which generalizes Breiman's method by allowing the linear parameters to vary with input features. This improvement enables NNS to take advantage of the fact that distinct base models often perform better at different regions of the feature space. Our method uses neural networks to estimate the stacking coefficients. We show that while our approach keeps the interpretative features of Breiman's method at a local level, it leads to better predictive power, especially in datasets with large sample sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge