Thee Chanyaswad
A compressive multi-kernel method for privacy-preserving machine learning
Jun 20, 2021


Abstract:As the analytic tools become more powerful, and more data are generated on a daily basis, the issue of data privacy arises. This leads to the study of the design of privacy-preserving machine learning algorithms. Given two objectives, namely, utility maximization and privacy-loss minimization, this work is based on two previously non-intersecting regimes -- Compressive Privacy and multi-kernel method. Compressive Privacy is a privacy framework that employs utility-preserving lossy-encoding scheme to protect the privacy of the data, while multi-kernel method is a kernel based machine learning regime that explores the idea of using multiple kernels for building better predictors. The compressive multi-kernel method proposed consists of two stages -- the compression stage and the multi-kernel stage. The compression stage follows the Compressive Privacy paradigm to provide the desired privacy protection. Each kernel matrix is compressed with a lossy projection matrix derived from the Discriminant Component Analysis (DCA). The multi-kernel stage uses the signal-to-noise ratio (SNR) score of each kernel to non-uniformly combine multiple compressive kernels. The proposed method is evaluated on two mobile-sensing datasets -- MHEALTH and HAR -- where activity recognition is defined as utility and person identification is defined as privacy. The results show that the compression regime is successful in privacy preservation as the privacy classification accuracies are almost at the random-guess level in all experiments. On the other hand, the novel SNR-based multi-kernel shows utility classification accuracy improvement upon the state-of-the-art in both datasets. These results indicate a promising direction for research in privacy-preserving machine learning.
MVG Mechanism: Differential Privacy under Matrix-Valued Query
Oct 16, 2018



Abstract:Differential privacy mechanism design has traditionally been tailored for a scalar-valued query function. Although many mechanisms such as the Laplace and Gaussian mechanisms can be extended to a matrix-valued query function by adding i.i.d. noise to each element of the matrix, this method is often suboptimal as it forfeits an opportunity to exploit the structural characteristics typically associated with matrix analysis. To address this challenge, we propose a novel differential privacy mechanism called the Matrix-Variate Gaussian (MVG) mechanism, which adds a matrix-valued noise drawn from a matrix-variate Gaussian distribution, and we rigorously prove that the MVG mechanism preserves $(\epsilon,\delta)$-differential privacy. Furthermore, we introduce the concept of directional noise made possible by the design of the MVG mechanism. Directional noise allows the impact of the noise on the utility of the matrix-valued query function to be moderated. Finally, we experimentally demonstrate the performance of our mechanism using three matrix-valued queries on three privacy-sensitive datasets. We find that the MVG mechanism notably outperforms four previous state-of-the-art approaches, and provides comparable utility to the non-private baseline.
* Appeared in CCS'18
Supervising Nyström Methods via Negative Margin Support Vector Selection
May 18, 2018
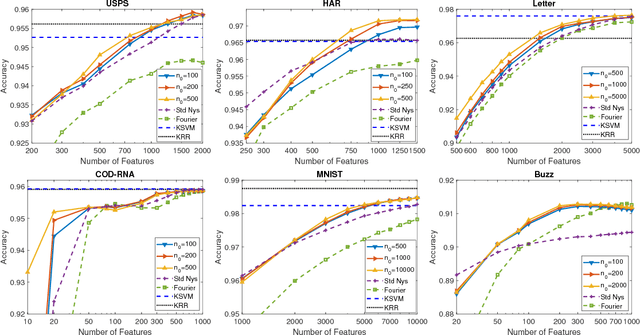
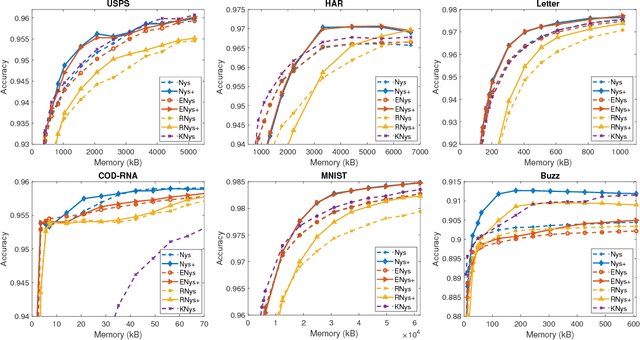
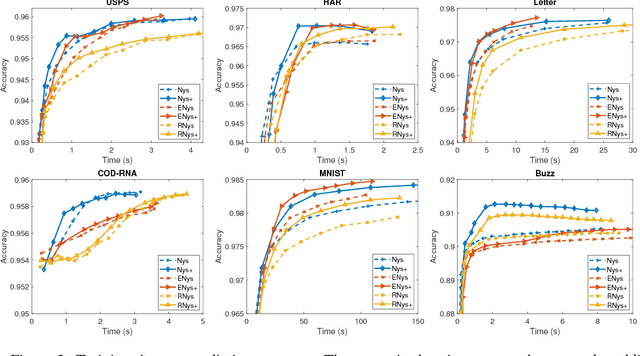
Abstract:The Nystr\"om methods have been popular techniques for scalable kernel based learning. They approximate explicit, low-dimensional feature mappings for kernel functions from the pairwise comparisons with the training data. However, Nystr\"om methods are generally applied without the supervision provided by the training labels in the classification/regression problems. This leads to pairwise comparisons with randomly chosen training samples in the model. Conversely, this work studies a supervised Nystr\"om method that chooses the critical subsets of samples for the success of the Machine Learning model. Particularly, we select the Nystr\"om support vectors via the negative margin criterion, and create explicit feature maps that are more suitable for the classification task on the data. Experimental results on six datasets show that, without increasing the complexity over unsupervised techniques, our method can significantly improve the classification performance achieved via kernel approximation methods and reduce the number of features needed to reach or exceed the performance of the full-dimensional kernel machines.
A Differential Privacy Mechanism Design Under Matrix-Valued Query
Feb 26, 2018



Abstract:Traditionally, differential privacy mechanism design has been tailored for a scalar-valued query function. Although many mechanisms such as the Laplace and Gaussian mechanisms can be extended to a matrix-valued query function by adding i.i.d. noise to each element of the matrix, this method is often sub-optimal as it forfeits an opportunity to exploit the structural characteristics typically associated with matrix analysis. In this work, we consider the design of differential privacy mechanism specifically for a matrix-valued query function. The proposed solution is to utilize a matrix-variate noise, as opposed to the traditional scalar-valued noise. Particularly, we propose a novel differential privacy mechanism called the Matrix-Variate Gaussian (MVG) mechanism, which adds a matrix-valued noise drawn from a matrix-variate Gaussian distribution. We prove that the MVG mechanism preserves $(\epsilon,\delta)$-differential privacy, and show that it allows the structural characteristics of the matrix-valued query function to naturally be exploited. Furthermore, due to the multi-dimensional nature of the MVG mechanism and the matrix-valued query, we introduce the concept of directional noise, which can be utilized to mitigate the impact the noise has on the utility of the query. Finally, we demonstrate the performance of the MVG mechanism and the advantages of directional noise using three matrix-valued queries on three privacy-sensitive datasets. We find that the MVG mechanism notably outperforms four previous state-of-the-art approaches, and provides comparable utility to the non-private baseline. Our work thus presents a promising prospect for both future research and implementation of differential privacy for matrix-valued query functions.
Desensitized RDCA Subspaces for Compressive Privacy in Machine Learning
Jul 24, 2017



Abstract:The quest for better data analysis and artificial intelligence has lead to more and more data being collected and stored. As a consequence, more data are exposed to malicious entities. This paper examines the problem of privacy in machine learning for classification. We utilize the Ridge Discriminant Component Analysis (RDCA) to desensitize data with respect to a privacy label. Based on five experiments, we show that desensitization by RDCA can effectively protect privacy (i.e. low accuracy on the privacy label) with small loss in utility. On HAR and CMU Faces datasets, the use of desensitized data results in random guess level accuracies for privacy at a cost of 5.14% and 0.04%, on average, drop in the utility accuracies. For Semeion Handwritten Digit dataset, accuracies of the privacy-sensitive digits are almost zero, while the accuracies for the utility-relevant digits drop by 7.53% on average. This presents a promising solution to the problem of privacy in machine learning for classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge