GLIDE-RL: Grounded Language Instruction through DEmonstration in RL

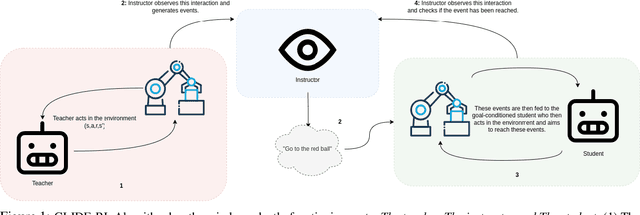
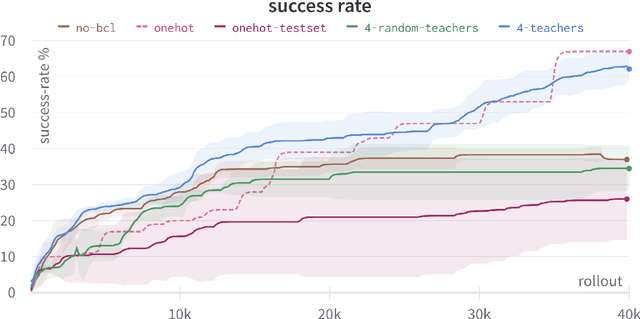
One of the final frontiers in the development of complex human - AI collaborative systems is the ability of AI agents to comprehend the natural language and perform tasks accordingly. However, training efficient Reinforcement Learning (RL) agents grounded in natural language has been a long-standing challenge due to the complexity and ambiguity of the language and sparsity of the rewards, among other factors. Several advances in reinforcement learning, curriculum learning, continual learning, language models have independently contributed to effective training of grounded agents in various environments. Leveraging these developments, we present a novel algorithm, Grounded Language Instruction through DEmonstration in RL (GLIDE-RL) that introduces a teacher-instructor-student curriculum learning framework for training an RL agent capable of following natural language instructions that can generalize to previously unseen language instructions. In this multi-agent framework, the teacher and the student agents learn simultaneously based on the student's current skill level. We further demonstrate the necessity for training the student agent with not just one, but multiple teacher agents. Experiments on a complex sparse reward environment validates the effectiveness of our proposed approach.

Nonnegative Low-Rank Tensor Completion via Dual Formulation with Applications to Image and Video Completion

Recent approaches to the tensor completion problem have often overlooked the nonnegative structure of the data. We consider the problem of learning a nonnegative low-rank tensor, and using duality theory, we propose a novel factorization of such tensors. The factorization decouples the nonnegative constraints from the low-rank constraints. The resulting problem is an optimization problem on manifolds, and we propose a variant of Riemannian conjugate gradients to solve it. We test the proposed algorithm across various tasks such as colour image inpainting, video completion, and hyperspectral image completion. Experimental results show that the proposed method outperforms many state-of-the-art tensor completion algorithms.

Structured Low-Rank Tensor Learning

We consider the problem of learning low-rank tensors from partial observations with structural constraints, and propose a novel factorization of such tensors, which leads to a simpler optimization problem. The resulting problem is an optimization problem on manifolds. We develop first-order and second-order Riemannian optimization algorithms to solve it. The duality gap for the resulting problem is derived, and we experimentally verify the correctness of the proposed algorithm. We demonstrate the algorithm on nonnegative constraints and Hankel constraints.

On Riemannian Approach for Constrained Optimization Model in Extreme Classification Problems

We propose a novel Riemannian method for solving the Extreme multi-label classification problem that exploits the geometric structure of the sparse low-dimensional local embedding models. A constrained optimization problem is formulated as an optimization problem on matrix manifold and solved using a Riemannian optimization method. The proposed approach is tested on several real world large scale multi-label datasets and its usefulness is demonstrated through numerical experiments. The numerical experiments suggest that the proposed method is fastest to train and has least model size among the embedding-based methods. An outline of the proof of convergence for the proposed Riemannian optimization method is also stated.