Scaling Up Graph Neural Networks Via Graph Coarsening

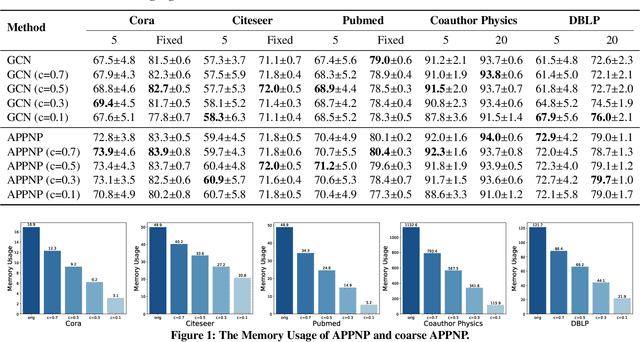
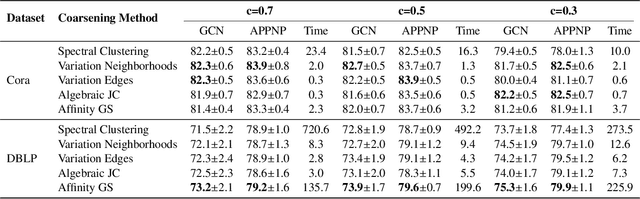
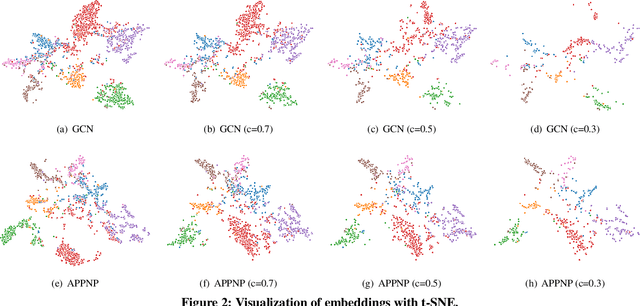
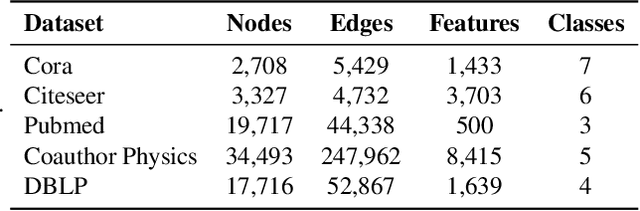
Scalability of graph neural networks remains one of the major challenges in graph machine learning. Since the representation of a node is computed by recursively aggregating and transforming representation vectors of its neighboring nodes from previous layers, the receptive fields grow exponentially, which makes standard stochastic optimization techniques ineffective. Various approaches have been proposed to alleviate this issue, e.g., sampling-based methods and techniques based on pre-computation of graph filters. In this paper, we take a different approach and propose to use graph coarsening for scalable training of GNNs, which is generic, extremely simple and has sublinear memory and time costs during training. We present extensive theoretical analysis on the effect of using coarsening operations and provides useful guidance on the choice of coarsening methods. Interestingly, our theoretical analysis shows that coarsening can also be considered as a type of regularization and may improve the generalization. Finally, empirical results on real world datasets show that, simply applying off-the-shelf coarsening methods, we can reduce the number of nodes by up to a factor of ten without causing a noticeable downgrade in classification accuracy.

Graph Neural Networks Inspired by Classical Iterative Algorithms

Despite the recent success of graph neural networks (GNN), common architectures often exhibit significant limitations, including sensitivity to oversmoothing, long-range dependencies, and spurious edges, e.g., as can occur as a result of graph heterophily or adversarial attacks. To at least partially address these issues within a simple transparent framework, we consider a new family of GNN layers designed to mimic and integrate the update rules of two classical iterative algorithms, namely, proximal gradient descent and iterative reweighted least squares (IRLS). The former defines an extensible base GNN architecture that is immune to oversmoothing while nonetheless capturing long-range dependencies by allowing arbitrary propagation steps. In contrast, the latter produces a novel attention mechanism that is explicitly anchored to an underlying end-toend energy function, contributing stability with respect to edge uncertainty. When combined we obtain an extremely simple yet robust model that we evaluate across disparate scenarios including standardized benchmarks, adversarially-perturbated graphs, graphs with heterophily, and graphs involving long-range dependencies. In doing so, we compare against SOTA GNN approaches that have been explicitly designed for the respective task, achieving competitive or superior node classification accuracy.