Integrated Communication and Computing in Time-Varying mmWave Channels

We propose a novel framework for integrated communication and computing (ICC) transceiver design in time-varying millimeter-wave (mmWave) channels. In particular, in order to cope with the dynamics of time-varying mmWave channels, the detection of communication symbols and the execution of an over-the-air computing (AirComp) operation are performed in parallel with channel tracking, as opposed to existing state-of-the-art (SotA) on ICC where perfect knowledge of the channel at all time instances is typically assumed. For clarity of exposition, we consider a single-input multiple-output (SIMO) uplink scenario where multiple single-antenna user equipment (UE) transmit to a base station (BS) equipped with multiple antennas, such that each UE, or edge device (ED), precodes its own transmit signal, while the BS, or access points (APs), also performs receive beamforming. The proposed transceiver framework then estimates channel state information (CSI) and data symbols in parallel, using a bilinear Gaussian belief propagation (BiGaBP) algorithm for joint channel and data detection (JCDE), aided by a channel prediction (CP) algorithm executed before each estimation window at the BS. The AirComp operation is then executed by means of an optimal combination of the residual signal. Simulation results demonstrate the effectiveness of the proposed scheme in performing ICC in challenging time-varying mmWave channels, with minimal degradation to both communication and computing performance.

Quaternion-Domain Super MDS for Robust 3D Localization

This paper proposes a novel low-complexity three-dimensional (3D) localization algorithm for wireless sensor networks, termed quanternion-domain super multi-dimensional scaling (QD-SMDS). The algorithm is based on a reformulation of the SMDS, originally developed in the real domain, using quaternion algebra. By representing 3D coordinates as quaternions, the method constructs a rank-1 Gram edge kernel (GEK) matrix that integrates both relative distance and angular information between nodes, which enhances the noise reduction effect achieved through low-rank truncation employing singular value decomposition (SVD), thereby improving robustness against information loss. To further reduce computational complexity, we also propose a variant of QD-SMDS that eliminates the need for the computationally expensive SVD by leveraging the inherent structure of the quaternion-domain GEK matrix. This alternative directly estimates node coordinates using only matrix multiplications within the quaternion domain. Simulation results demonstrate that the proposed method significantly improves localization accuracy compared to the original SMDS algorithm, especially in scenarios with substantial measurement errors. The proposed method also achieves comparable localization accuracy without requiring SVD.

A Flexible Design Framework for Integrated Communication and Computing Receivers

We propose a framework to design integrated communication and computing (ICC) receivers capable of simultaneously detecting data symbols and performing over-the-air computing (AirComp) in a manner that: a) is systematically generalizable to any nomographic function, b) scales to a massive number of user equipments (UEs) and edge devices (EDs), c) supports the computation of multiple independent functions (streams), and d) operates in a multi-access fashion whereby each transmitter can choose to transmit either data symbols, computing signals or both. For the sake of illustration, we design the proposed multi-stream and multi-access method under an uplink setting, where multiple single-antenna UEs/EDs simultaneously transmit data and computing signals to a single multiple-antenna base station (BS)/access point (AP). Under the communication functionality, the receiver aims to detect all independent communication symbols while treating the computing streams as aggregate interference which it seeks to mitigate; and conversely, under the computing functionality, to minimize the distortion over the computing streams while minimizing their mutual interference as well as the interference due to data symbols. To that end, the design leverages the Gaussian belief propagation (GaBP) framework relying only on element-wise scalar operations coupled with closed-form combiners purpose-built for the AirComp operation, which allows for its use in massive settings, as demonstrated by simulation results incorporating up to 200 antennas and 300 UEs/EDs. The efficacy of the proposed method under different loading conditions is also evaluated, with the performance of the scheme shown to approach fundamental limiting bounds in the under/fully loaded cases.

Quaternion Domain Super MDS for 3D Localization

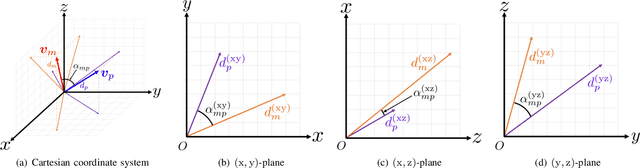
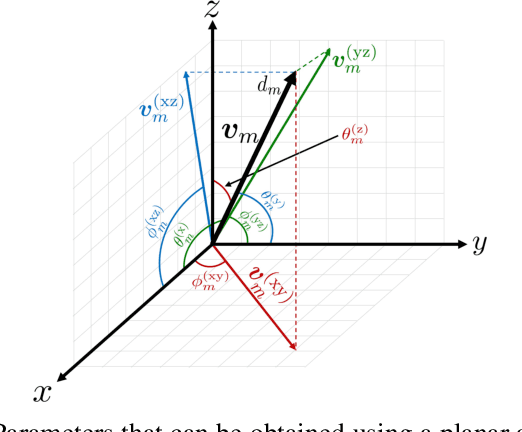
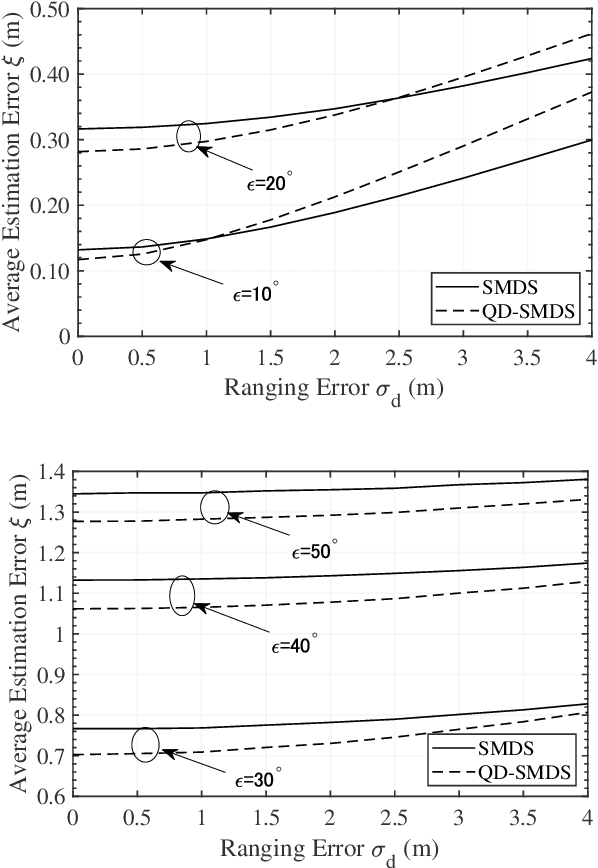
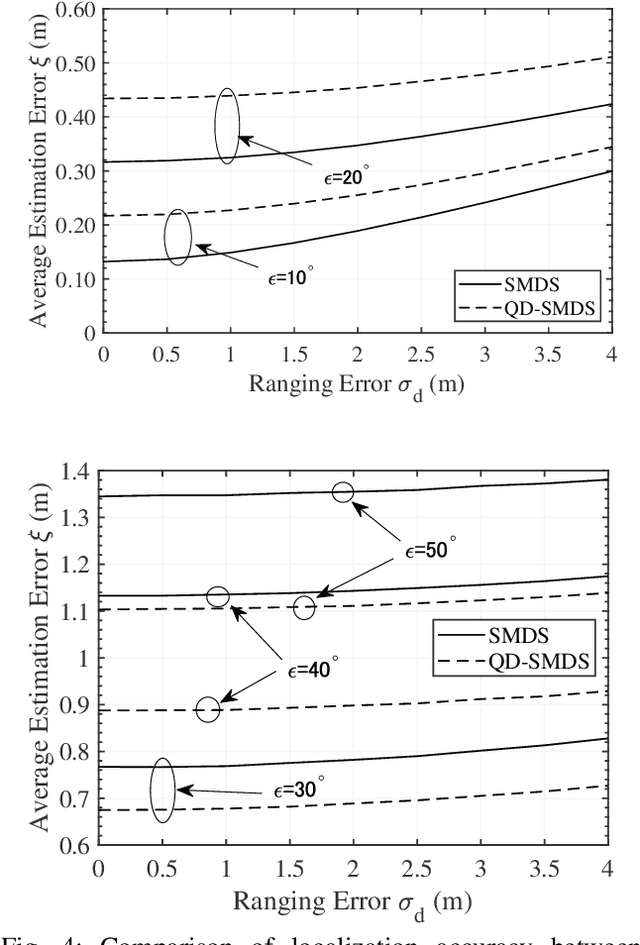
We propose a novel low-complexity three-dimensional (3D) localization algorithm for wireless sensor networks, termed quaternion-domain super multidimensional scaling (QD-SMDS). This algorithm reformulates the conventional SMDS, which was originally developed in the real domain, into the quaternion domain. By representing 3D coordinates as quaternions, the method enables the construction of a rank-1 Gram edge kernel (GEK) matrix that integrates both relative distance and angular (phase) information between nodes, maximizing the noise reduction effect achieved through low-rank truncation via singular value decomposition (SVD). The simulation results indicate that the proposed method demonstrates a notable enhancement in localization accuracy relative to the conventional SMDS algorithm, particularly in scenarios characterized by substantial measurement errors.

Discrete-Valued Signal Estimation via Low-Complexity Message Passing Algorithm for Highly Correlated Measurements

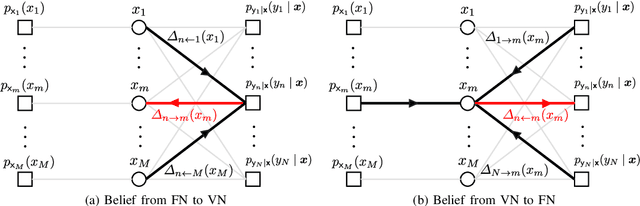
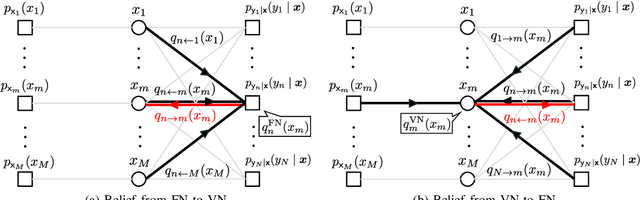
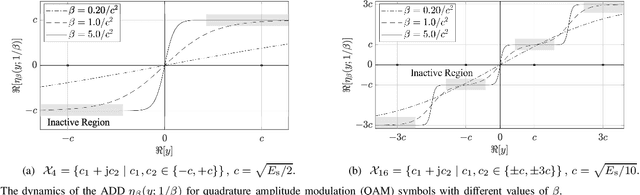
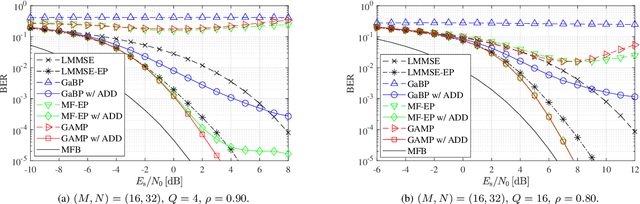
This paper considers a discrete-valued signal estimation scheme based on a low-complexity Bayesian optimal message passing algorithm (MPA) for solving massive linear inverse problems under highly correlated measurements. Gaussian belief propagation (GaBP) can be derived by applying the central limit theorem (CLT)-based Gaussian approximation to the sum-product algorithm (SPA) operating on a dense factor graph (FG), while matched filter (MF)-expectation propagation (EP) can be obtained based on the EP framework tailored for the same FG. Generalized approximate message passing (GAMP) can be found by applying a rigorous approximation technique for both of them in the large-system limit, and these three MPAs perform signal detection using MF by assuming large-scale uncorrelated observations. However, each of them has a different inherent self-noise suppression mechanism, which makes a significant difference in the robustness against the correlation of the observations when we apply an annealed discrete denoiser (ADD) that adaptively controls its nonlinearity with the inverse temperature parameter corresponding to the number of iterations. In this paper, we unravel the mechanism of this interesting phenomenon, and further demonstrate the practical applicability of the low-complexity Bayesian optimal MPA with ADD under highly correlated measurements.

Massive Index Modulation with Combinatorics-Free Detection for Integrated Sensing and Communications

Integrated sensing and communications (ISAC) and index modulation (IM) are promising technologies for beyond fifth generation (B5G) and sixth generation (6G) systems. While ISAC enables new applications, IM is attractive for its inherent energy and spectral efficiencies. In this article we propose massive IM as an enabler of ISAC, by considering transmit signals with information conveyed through the indexation of the resources utilized in their transmission, and pilot symbols exploited for sensing. In order to overcome the complexity hurdle arising from the large sizes of IM codebooks, we propose a novel message passing (MP) decoder designed under the Gaussian belief propagation (GaBP) framework exploiting a novel unit vector decomposition (UVD) of IM signals with purpose-derived novel probability distributions. The proposed method enjoys a low decoding complexity that is independent of combinatorial factors, while still approaching the performance of unfeasible state-of-the-art (SotA) search-based methods. The effectiveness of the proposed approach is demonstrated via complexity analysis and numerical results for piloted generalized quadrature spatial modulation (GQSM) systems of large sizes (up to 96 antennas).

Joint Channel, Data and Radar Parameter Estimation for AFDM Systems in Doubly-Dispersive Channels

We propose new schemes for joint channel and data estimation (JCDE) and radar parameter estimation (RPE) in doubly-dispersive channels, such that integrated sensing and communications (ISAC) is enabled by user equipment (UE) independently performing JCDE, and base stations (BSs) performing RPE. The contributed JCDE and RPE schemes are designed for waveforms known to perform well in doubly-dispersive channels, under a unified model that captures the features of either legacy orthogonal frequency division multiplexing (OFDM), state-of-the-art (SotA) orthogonal time frequency space (OTFS), and next-generation affine frequency division multiplexing (AFDM) systems. The proposed JCDE algorithm is based on a Bayesian parametric bilinear Gaussian belief propagation (PBiGaBP) framework first proposed for OTFS and here shown to apply to all aforementioned waveforms, while the RPE scheme is based on a new probabilistic data association (PDA) approach incorporating a Bernoulli-Gaussian denoising, optimized via expectation maximization (EM). Simulation results demonstrate that JCDE in AFDM systems utilizing a single pilot per block significantly outperforms the SotA alternative even if the latter is granted a substantial power advantage. Similarly, the AFDM-based RPE scheme is found to outperform the OTFS-based approach, as well as the sparse Bayesian learning (SBL) technique, regardless of the waveform used.