Vector Similarity Search-Based MCS Selection in Massive Multi-User MIMO-OFDM

This paper proposes a novel modulation and coding scheme (MCS) selection framework that integrates mutual information (MI) prediction based on vector similarity search (VSS) for massive multi-user multiple-input multiple-output orthogonal frequency-division multiplexing (MU-MIMO-OFDM) systems with advanced uplink multi-user detection (MUD). The framework performs MCS selection at the transport block (TB)-level MI and establishes the mapping from post-MUD MI to post-decoding block error rate (BLER) using a prediction function generated from extrinsic information transfer (EXIT) curves. A key innovation is the VSS-based MI prediction scheme, which addresses the challenge of analytically predicting MI in iterative detectors such as expectation propagation (EP). In this scheme, an offline vector database (VDB) stores feature vectors derived from channel state information (CSI) and average received signal-to-noise ratio (SNR), together with corresponding MI values achieved with advanced MUD. During online operation, an approximate nearest neighbor (ANN) search on graphics processing units (GPUs) enables ultra-fast and accurate MI prediction, effectively capturing iterative detection gains. Simulation results under fifth-generation new radio (5G NR)-compliant settings demonstrate that the proposed framework significantly improves both system and user throughput, ensuring that the detection gains of advanced MUD are faithfully translated into tangible system-level performance improvements.

Discrete-Valued Signal Estimation via Low-Complexity Message Passing Algorithm for Highly Correlated Measurements

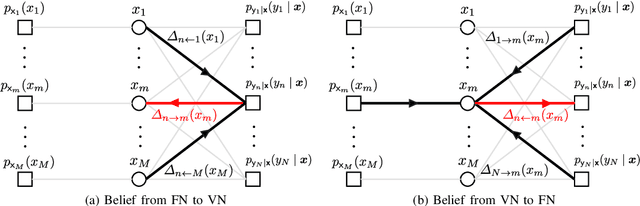
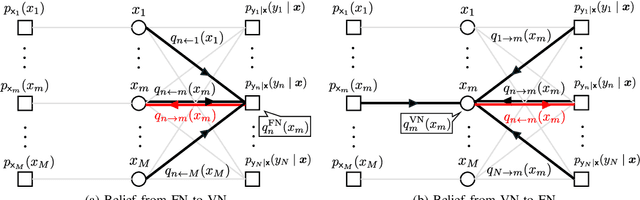
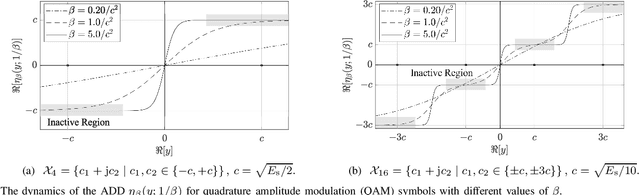
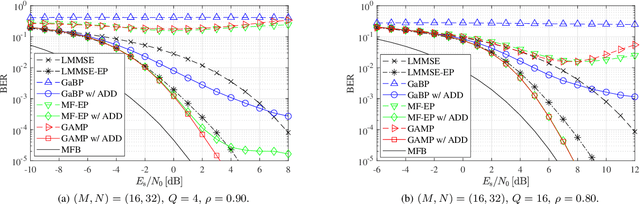
This paper considers a discrete-valued signal estimation scheme based on a low-complexity Bayesian optimal message passing algorithm (MPA) for solving massive linear inverse problems under highly correlated measurements. Gaussian belief propagation (GaBP) can be derived by applying the central limit theorem (CLT)-based Gaussian approximation to the sum-product algorithm (SPA) operating on a dense factor graph (FG), while matched filter (MF)-expectation propagation (EP) can be obtained based on the EP framework tailored for the same FG. Generalized approximate message passing (GAMP) can be found by applying a rigorous approximation technique for both of them in the large-system limit, and these three MPAs perform signal detection using MF by assuming large-scale uncorrelated observations. However, each of them has a different inherent self-noise suppression mechanism, which makes a significant difference in the robustness against the correlation of the observations when we apply an annealed discrete denoiser (ADD) that adaptively controls its nonlinearity with the inverse temperature parameter corresponding to the number of iterations. In this paper, we unravel the mechanism of this interesting phenomenon, and further demonstrate the practical applicability of the low-complexity Bayesian optimal MPA with ADD under highly correlated measurements.