Discrete-Valued Signal Estimation via Low-Complexity Message Passing Algorithm for Highly Correlated Measurements
Paper and Code
Nov 13, 2024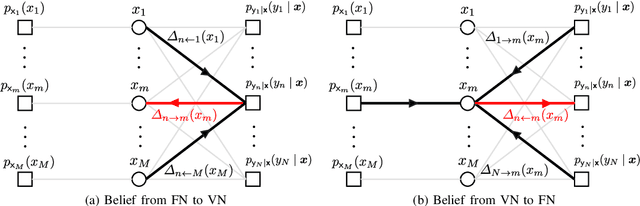
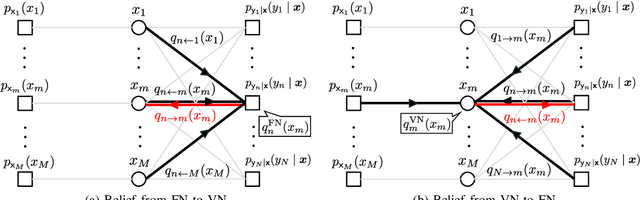
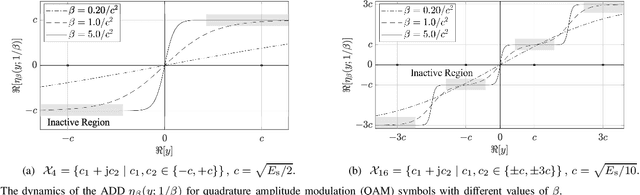
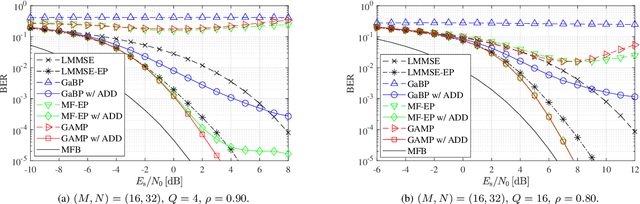
This paper considers a discrete-valued signal estimation scheme based on a low-complexity Bayesian optimal message passing algorithm (MPA) for solving massive linear inverse problems under highly correlated measurements. Gaussian belief propagation (GaBP) can be derived by applying the central limit theorem (CLT)-based Gaussian approximation to the sum-product algorithm (SPA) operating on a dense factor graph (FG), while matched filter (MF)-expectation propagation (EP) can be obtained based on the EP framework tailored for the same FG. Generalized approximate message passing (GAMP) can be found by applying a rigorous approximation technique for both of them in the large-system limit, and these three MPAs perform signal detection using MF by assuming large-scale uncorrelated observations. However, each of them has a different inherent self-noise suppression mechanism, which makes a significant difference in the robustness against the correlation of the observations when we apply an annealed discrete denoiser (ADD) that adaptively controls its nonlinearity with the inverse temperature parameter corresponding to the number of iterations. In this paper, we unravel the mechanism of this interesting phenomenon, and further demonstrate the practical applicability of the low-complexity Bayesian optimal MPA with ADD under highly correlated measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge