Rethinking the Backbone in Class Imbalanced Federated Source Free Domain Adaptation: The Utility of Vision Foundation Models

Federated Learning (FL) offers a framework for training models collaboratively while preserving data privacy of each client. Recently, research has focused on Federated Source-Free Domain Adaptation (FFREEDA), a more realistic scenario wherein client-held target domain data remains unlabeled, and the server can access source domain data only during pre-training. We extend this framework to a more complex and realistic setting: Class Imbalanced FFREEDA (CI-FFREEDA), which takes into account class imbalances in both the source and target domains, as well as label shifts between source and target and among target clients. The replication of existing methods in our experimental setup lead us to rethink the focus from enhancing aggregation and domain adaptation methods to improving the feature extractors within the network itself. We propose replacing the FFREEDA backbone with a frozen vision foundation model (VFM), thereby improving overall accuracy without extensive parameter tuning and reducing computational and communication costs in federated learning. Our experimental results demonstrate that VFMs effectively mitigate the effects of domain gaps, class imbalances, and even non-IID-ness among target clients, suggesting that strong feature extractors, not complex adaptation or FL methods, are key to success in the real-world FL.

Robust Deepfake Detection for Electronic Know Your Customer Systems Using Registered Images

In this paper, we present a deepfake detection algorithm specifically designed for electronic Know Your Customer (eKYC) systems. To ensure the reliability of eKYC systems against deepfake attacks, it is essential to develop a robust deepfake detector capable of identifying both face swapping and face reenactment, while also being robust to image degradation. We address these challenges through three key contributions: (1)~Our approach evaluates the video's authenticity by detecting temporal inconsistencies in identity vectors extracted by face recognition models, leading to comprehensive detection of both face swapping and face reenactment. (2)~In addition to processing video input, the algorithm utilizes a registered image (assumed to be genuine) to calculate identity discrepancies between the input video and the registered image, significantly improving detection accuracy. (3)~We find that employing a face feature extractor trained on a larger dataset enhances both detection performance and robustness against image degradation. Our experimental results show that our proposed method accurately detects both face swapping and face reenactment comprehensively and is robust against various forms of unseen image degradation. Our source code is publicly available https://github.com/TaikiMiyagawa/DeepfakeDetection4eKYC.

Learning the Optimal Stopping for Early Classification within Finite Horizons via Sequential Probability Ratio Test

Time-sensitive machine learning benefits from Sequential Probability Ratio Test (SPRT), which provides an optimal stopping time for early classification of time series. However, in finite horizon scenarios, where input lengths are finite, determining the optimal stopping rule becomes computationally intensive due to the need for backward induction, limiting practical applicability. We thus introduce FIRMBOUND, an SPRT-based framework that efficiently estimates the solution to backward induction from training data, bridging the gap between optimal stopping theory and real-world deployment. It employs density ratio estimation and convex function learning to provide statistically consistent estimators for sufficient statistic and conditional expectation, both essential for solving backward induction; consequently, FIRMBOUND minimizes Bayes risk to reach optimality. Additionally, we present a faster alternative using Gaussian process regression, which significantly reduces training time while retaining low deployment overhead, albeit with potential compromise in statistical consistency. Experiments across independent and identically distributed (i.i.d.), non-i.i.d., binary, multiclass, synthetic, and real-world datasets show that FIRMBOUND achieves optimalities in the sense of Bayes risk and speed-accuracy tradeoff. Furthermore, it advances the tradeoff boundary toward optimality when possible and reduces decision-time variance, ensuring reliable decision-making. Code is publicly available at https://github.com/Akinori-F-Ebihara/FIRMBOUND

Federated Source-free Domain Adaptation for Classification: Weighted Cluster Aggregation for Unlabeled Data

Federated learning (FL) commonly assumes that the server or some clients have labeled data, which is often impractical due to annotation costs and privacy concerns. Addressing this problem, we focus on a source-free domain adaptation task, where (1) the server holds a pre-trained model on labeled source domain data, (2) clients possess only unlabeled data from various target domains, and (3) the server and clients cannot access the source data in the adaptation phase. This task is known as Federated source-Free Domain Adaptation (FFREEDA). Specifically, we focus on classification tasks, while the previous work solely studies semantic segmentation. Our contribution is the novel Federated learning with Weighted Cluster Aggregation (FedWCA) method, designed to mitigate both domain shifts and privacy concerns with only unlabeled data. FedWCA comprises three phases: private and parameter-free clustering of clients to obtain domain-specific global models on the server, weighted aggregation of the global models for the clustered clients, and local domain adaptation with pseudo-labeling. Experimental results show that FedWCA surpasses several existing methods and baselines in FFREEDA, establishing its effectiveness and practicality.

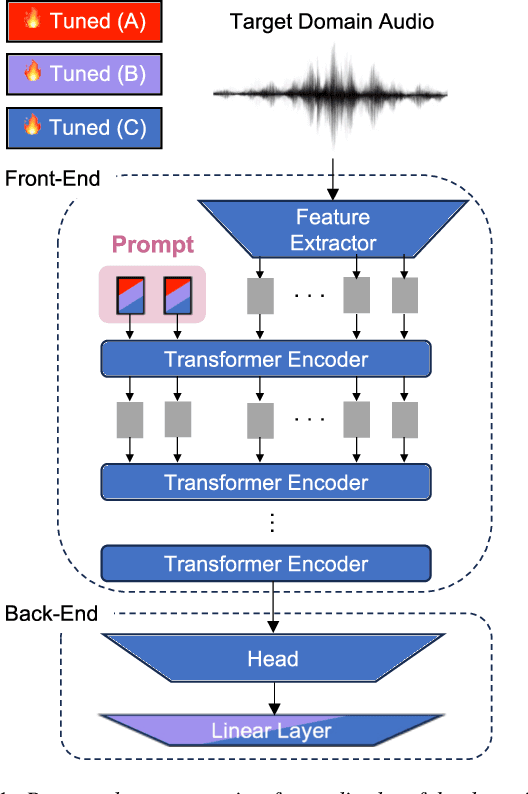
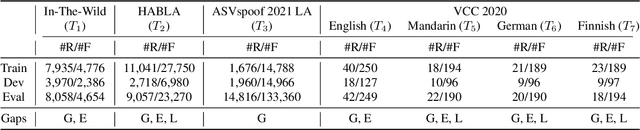
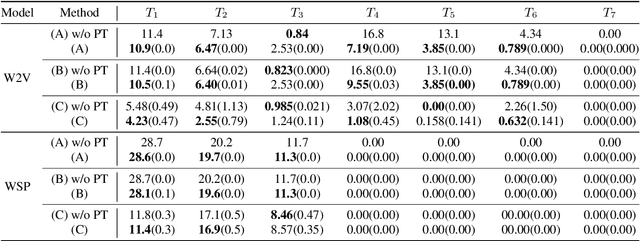
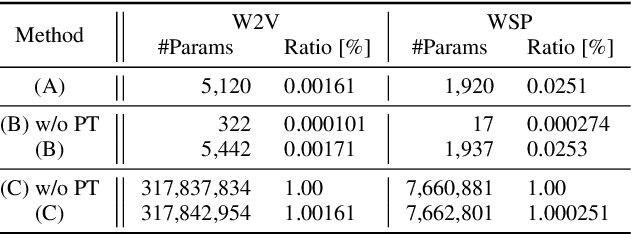
Prompt Tuning for Audio Deepfake Detection: Computationally Efficient Test-time Domain Adaptation with Limited Target Dataset

We study test-time domain adaptation for audio deepfake detection (ADD), addressing three challenges: (i) source-target domain gaps, (ii) limited target dataset size, and (iii) high computational costs. We propose an ADD method using prompt tuning in a plug-in style. It bridges domain gaps by integrating it seamlessly with state-of-the-art transformer models and/or with other fine-tuning methods, boosting their performance on target data (challenge (i)). In addition, our method can fit small target datasets because it does not require a large number of extra parameters (challenge (ii)). This feature also contributes to computational efficiency, countering the high computational costs typically associated with large-scale pre-trained models in ADD (challenge (iii)). We conclude that prompt tuning for ADD under domain gaps presents a promising avenue for enhancing accuracy with minimal target data and negligible extra computational burden.

Multi-Object Tracking as Attention Mechanism

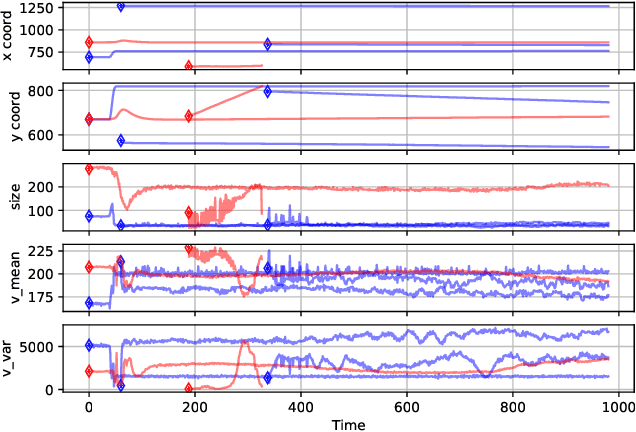
We propose a conceptually simple and thus fast multi-object tracking (MOT) model that does not require any attached modules, such as the Kalman filter, Hungarian algorithm, transformer blocks, or graph networks. Conventional MOT models are built upon the multi-step modules listed above, and thus the computational cost is high. Our proposed end-to-end MOT model, \textit{TicrossNet}, is composed of a base detector and a cross-attention module only. As a result, the overhead of tracking does not increase significantly even when the number of instances ($N_t$) increases. We show that TicrossNet runs \textit{in real-time}; specifically, it achieves 32.6 FPS on MOT17 and 31.0 FPS on MOT20 (Tesla V100), which includes as many as $>$100 instances per frame. We also demonstrate that TicrossNet is robust to $N_t$; thus, it does not have to change the size of the base detector, depending on $N_t$, as is often done by other models for real-time processing.

Toward Asymptotic Optimality: Sequential Unsupervised Regression of Density Ratio for Early Classification

Theoretically-inspired sequential density ratio estimation (SDRE) algorithms are proposed for the early classification of time series. Conventional SDRE algorithms can fail to estimate DRs precisely due to the internal overnormalization problem, which prevents the DR-based sequential algorithm, Sequential Probability Ratio Test (SPRT), from reaching its asymptotic Bayes optimality. Two novel SPRT-based algorithms, B2Bsqrt-TANDEM and TANDEMformer, are designed to avoid the overnormalization problem for precise unsupervised regression of SDRs. The two algorithms statistically significantly reduce DR estimation errors and classification errors on an artificial sequential Gaussian dataset and real datasets (SiW, UCF101, and HMDB51), respectively. The code is available at: https://github.com/Akinori-F-Ebihara/LLR_saturation_problem.

Toward Equation of Motion for Deep Neural Networks: Continuous-time Gradient Descent and Discretization Error Analysis

We derive and solve an ``Equation of Motion'' (EoM) for deep neural networks (DNNs), a differential equation that precisely describes the discrete learning dynamics of DNNs. Differential equations are continuous but have played a prominent role even in the study of discrete optimization (gradient descent (GD) algorithms). However, there still exist gaps between differential equations and the actual learning dynamics of DNNs due to discretization error. In this paper, we start from gradient flow (GF) and derive a counter term that cancels the discretization error between GF and GD. As a result, we obtain EoM, a continuous differential equation that precisely describes the discrete learning dynamics of GD. We also derive discretization error to show to what extent EoM is precise. In addition, we apply EoM to two specific cases: scale- and translation-invariant layers. EoM highlights differences between continuous-time and discrete-time GD, indicating the importance of the counter term for a better description of the discrete learning dynamics of GD. Our experimental results support our theoretical findings.

Convolutional Neural Networks for Time-dependent Classification of Variable-length Time Series

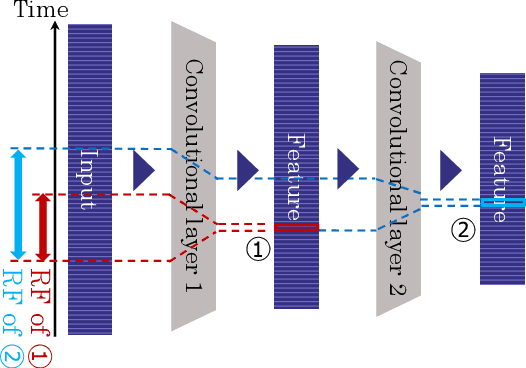
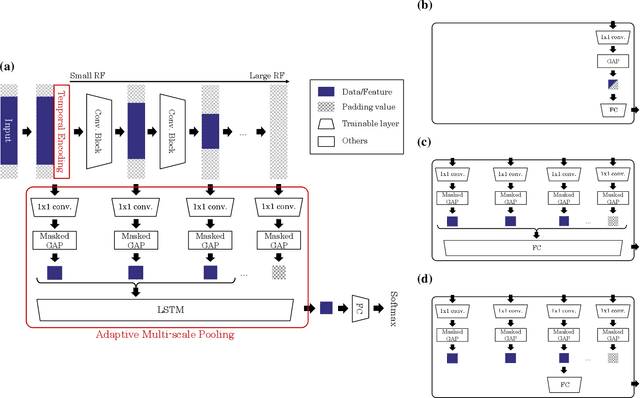
Time series data are often obtained only within a limited time range due to interruptions during observation process. To classify such partial time series, we need to account for 1) the variable-length data drawn from 2) different timestamps. To address the first problem, existing convolutional neural networks use global pooling after convolutional layers to cancel the length differences. This architecture suffers from the trade-off between incorporating entire temporal correlations in long data and avoiding feature collapse for short data. To resolve this tradeoff, we propose Adaptive Multi-scale Pooling, which aggregates features from an adaptive number of layers, i.e., only the first few layers for short data and more layers for long data. Furthermore, to address the second problem, we introduce Temporal Encoding, which embeds the observation timestamps into the intermediate features. Experiments on our private dataset and the UCR/UEA time series archive show that our modules improve classification accuracy especially on short data obtained as partial time series.

The Power of Log-Sum-Exp: Sequential Density Ratio Matrix Estimation for Speed-Accuracy Optimization

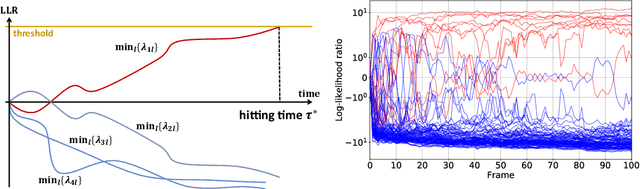
We propose a model for multiclass classification of time series to make a prediction as early and as accurate as possible. The matrix sequential probability ratio test (MSPRT) is known to be asymptotically optimal for this setting, but contains a critical assumption that hinders broad real-world applications; the MSPRT requires the underlying probability density. To address this problem, we propose to solve density ratio matrix estimation (DRME), a novel type of density ratio estimation that consists of estimating matrices of multiple density ratios with constraints and thus is more challenging than the conventional density ratio estimation. We propose a log-sum-exp-type loss function (LSEL) for solving DRME and prove the following: (i) the LSEL provides the true density ratio matrix as the sample size of the training set increases (consistency); (ii) it assigns larger gradients to harder classes (hard class weighting effect); and (iii) it provides discriminative scores even on class-imbalanced datasets (guess-aversion). Our overall architecture for early classification, MSPRT-TANDEM, statistically significantly outperforms baseline models on four datasets including action recognition, especially in the early stage of sequential observations. Our code and datasets are publicly available at: https://github.com/TaikiMiyagawa/MSPRT-TANDEM.