Constrained Entropic Unlearning: A Primal-Dual Framework for Large Language Models

Large Language Models (LLMs) deployed in real-world settings increasingly face the need to unlearn sensitive, outdated, or proprietary information. Existing unlearning methods typically formulate forgetting and retention as a regularized trade-off, combining both objectives into a single scalarized loss. This often leads to unstable optimization and degraded performance on retained data, especially under aggressive forgetting. We propose a new formulation of LLM unlearning as a constrained optimization problem: forgetting is enforced via a novel logit-margin flattening loss that explicitly drives the output distribution toward uniformity on a designated forget set, while retention is preserved through a hard constraint on a separate retain set. Compared to entropy-based objectives, our loss is softmax-free, numerically stable, and maintains non-vanishing gradients, enabling more efficient and robust optimization. We solve the constrained problem using a scalable primal-dual algorithm that exposes the trade-off between forgetting and retention through the dynamics of the dual variable. Evaluations on the TOFU and MUSE benchmarks across diverse LLM architectures demonstrate that our approach consistently matches or exceeds state-of-the-art baselines, effectively removing targeted information while preserving downstream utility.

Compositional Curvature Bounds for Deep Neural Networks

A key challenge that threatens the widespread use of neural networks in safety-critical applications is their vulnerability to adversarial attacks. In this paper, we study the second-order behavior of continuously differentiable deep neural networks, focusing on robustness against adversarial perturbations. First, we provide a theoretical analysis of robustness and attack certificates for deep classifiers by leveraging local gradients and upper bounds on the second derivative (curvature constant). Next, we introduce a novel algorithm to analytically compute provable upper bounds on the second derivative of neural networks. This algorithm leverages the compositional structure of the model to propagate the curvature bound layer-by-layer, giving rise to a scalable and modular approach. The proposed bound can serve as a differentiable regularizer to control the curvature of neural networks during training, thereby enhancing robustness. Finally, we demonstrate the efficacy of our method on classification tasks using the MNIST and CIFAR-10 datasets.

Gradient-Regularized Out-of-Distribution Detection

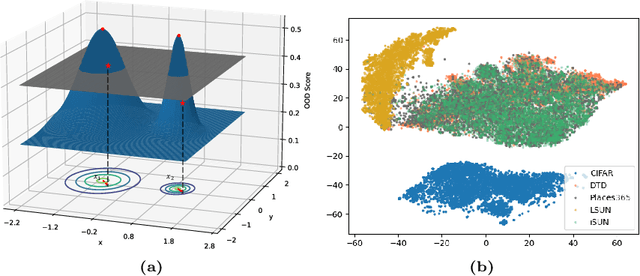
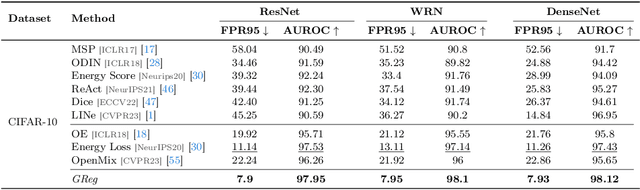
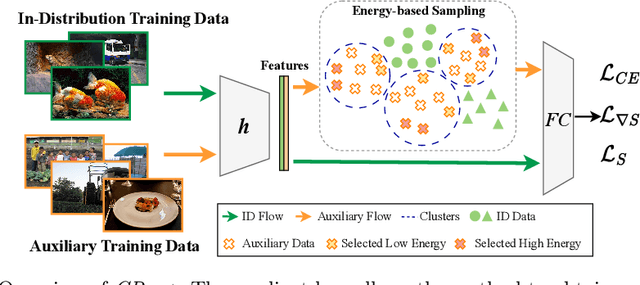
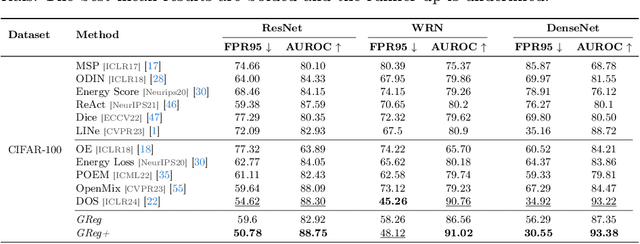
One of the challenges for neural networks in real-life applications is the overconfident errors these models make when the data is not from the original training distribution. Addressing this issue is known as Out-of-Distribution (OOD) detection. Many state-of-the-art OOD methods employ an auxiliary dataset as a surrogate for OOD data during training to achieve improved performance. However, these methods fail to fully exploit the local information embedded in the auxiliary dataset. In this work, we propose the idea of leveraging the information embedded in the gradient of the loss function during training to enable the network to not only learn a desired OOD score for each sample but also to exhibit similar behavior in a local neighborhood around each sample. We also develop a novel energy-based sampling method to allow the network to be exposed to more informative OOD samples during the training phase. This is especially important when the auxiliary dataset is large. We demonstrate the effectiveness of our method through extensive experiments on several OOD benchmarks, improving the existing state-of-the-art FPR95 by 4% on our ImageNet experiment. We further provide a theoretical analysis through the lens of certified robustness and Lipschitz analysis to showcase the theoretical foundation of our work. We will publicly release our code after the review process.

Certified Robustness via Dynamic Margin Maximization and Improved Lipschitz Regularization

To improve the robustness of deep classifiers against adversarial perturbations, many approaches have been proposed, such as designing new architectures with better robustness properties (e.g., Lipschitz-capped networks), or modifying the training process itself (e.g., min-max optimization, constrained learning, or regularization). These approaches, however, might not be effective at increasing the margin in the input (feature) space. As a result, there has been an increasing interest in developing training procedures that can directly manipulate the decision boundary in the input space. In this paper, we build upon recent developments in this category by developing a robust training algorithm whose objective is to increase the margin in the output (logit) space while regularizing the Lipschitz constant of the model along vulnerable directions. We show that these two objectives can directly promote larger margins in the input space. To this end, we develop a scalable method for calculating guaranteed differentiable upper bounds on the Lipschitz constant of neural networks accurately and efficiently. The relative accuracy of the bounds prevents excessive regularization and allows for more direct manipulation of the decision boundary. Furthermore, our Lipschitz bounding algorithm exploits the monotonicity and Lipschitz continuity of the activation layers, and the resulting bounds can be used to design new layers with controllable bounds on their Lipschitz constant. Experiments on the MNIST, CIFAR-10, and Tiny-ImageNet data sets verify that our proposed algorithm obtains competitively improved results compared to the state-of-the-art.

Automated Reachability Analysis of Neural Network-Controlled Systems via Adaptive Polytopes

Over-approximating the reachable sets of dynamical systems is a fundamental problem in safety verification and robust control synthesis. The representation of these sets is a key factor that affects the computational complexity and the approximation error. In this paper, we develop a new approach for over-approximating the reachable sets of neural network dynamical systems using adaptive template polytopes. We use the singular value decomposition of linear layers along with the shape of the activation functions to adapt the geometry of the polytopes at each time step to the geometry of the true reachable sets. We then propose a branch-and-bound method to compute accurate over-approximations of the reachable sets by the inferred templates. We illustrate the utility of the proposed approach in the reachability analysis of linear systems driven by neural network controllers.

ReachLipBnB: A branch-and-bound method for reachability analysis of neural autonomous systems using Lipschitz bounds

We propose a novel Branch-and-Bound method for reachability analysis of neural networks in both open-loop and closed-loop settings. Our idea is to first compute accurate bounds on the Lipschitz constant of the neural network in certain directions of interest offline using a convex program. We then use these bounds to obtain an instantaneous but conservative polyhedral approximation of the reachable set using Lipschitz continuity arguments. To reduce conservatism, we incorporate our bounding algorithm within a branching strategy to decrease the over-approximation error within an arbitrary accuracy. We then extend our method to reachability analysis of control systems with neural network controllers. Finally, to capture the shape of the reachable sets as accurately as possible, we use sample trajectories to inform the directions of the reachable set over-approximations using Principal Component Analysis (PCA). We evaluate the performance of the proposed method in several open-loop and closed-loop settings.