Safe Gradient Flow for Bilevel Optimization

Bilevel optimization is a key framework in hierarchical decision-making, where one problem is embedded within the constraints of another. In this work, we propose a control-theoretic approach to solving bilevel optimization problems. Our method consists of two components: a gradient flow mechanism to minimize the upper-level objective and a safety filter to enforce the constraints imposed by the lower-level problem. Together, these components form a safe gradient flow that solves the bilevel problem in a single loop. To improve scalability with respect to the lower-level problem's dimensions, we introduce a relaxed formulation and design a compact variant of the safe gradient flow. This variant minimizes the upper-level objective while ensuring the lower-level solution remains within a user-defined distance. Using Lyapunov analysis, we establish convergence guarantees for the dynamics, proving that they converge to a neighborhood of the optimal solution. Numerical experiments further validate the effectiveness of the proposed approaches. Our contributions provide both theoretical insights and practical tools for efficiently solving bilevel optimization problems.

Compositional Curvature Bounds for Deep Neural Networks

A key challenge that threatens the widespread use of neural networks in safety-critical applications is their vulnerability to adversarial attacks. In this paper, we study the second-order behavior of continuously differentiable deep neural networks, focusing on robustness against adversarial perturbations. First, we provide a theoretical analysis of robustness and attack certificates for deep classifiers by leveraging local gradients and upper bounds on the second derivative (curvature constant). Next, we introduce a novel algorithm to analytically compute provable upper bounds on the second derivative of neural networks. This algorithm leverages the compositional structure of the model to propagate the curvature bound layer-by-layer, giving rise to a scalable and modular approach. The proposed bound can serve as a differentiable regularizer to control the curvature of neural networks during training, thereby enhancing robustness. Finally, we demonstrate the efficacy of our method on classification tasks using the MNIST and CIFAR-10 datasets.

Provable Bounds on the Hessian of Neural Networks: Derivative-Preserving Reachability Analysis

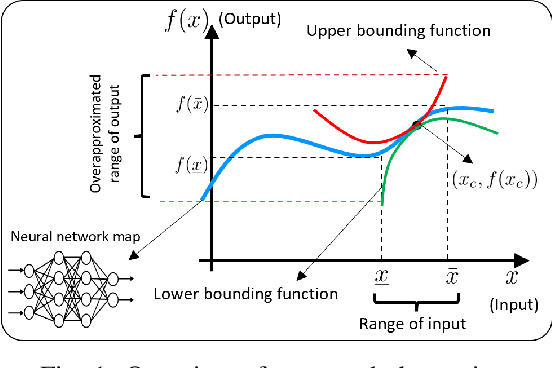
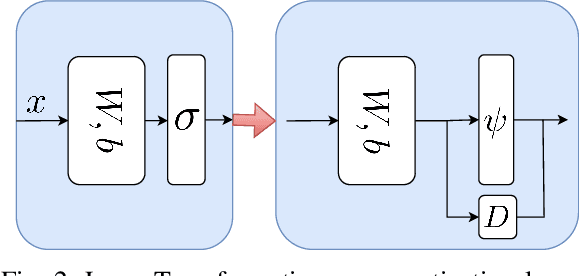
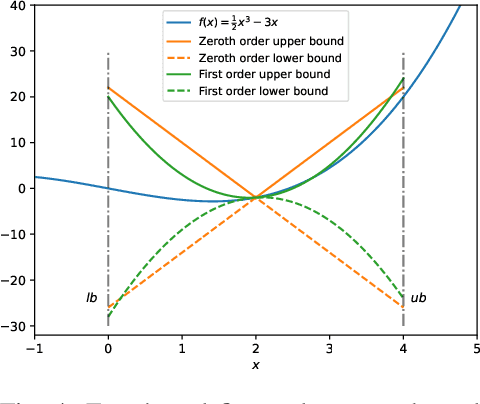
We propose a novel reachability analysis method tailored for neural networks with differentiable activations. Our idea hinges on a sound abstraction of the neural network map based on first-order Taylor expansion and bounding the remainder. To this end, we propose a method to compute analytical bounds on the network's first derivative (gradient) and second derivative (Hessian). A key aspect of our method is loop transformation on the activation functions to exploit their monotonicity effectively. The resulting end-to-end abstraction locally preserves the derivative information, yielding accurate bounds on small input sets. Finally, we employ a branch and bound framework for larger input sets to refine the abstraction recursively. We evaluate our method numerically via different examples and compare the results with relevant state-of-the-art methods.

Gradient-Regularized Out-of-Distribution Detection

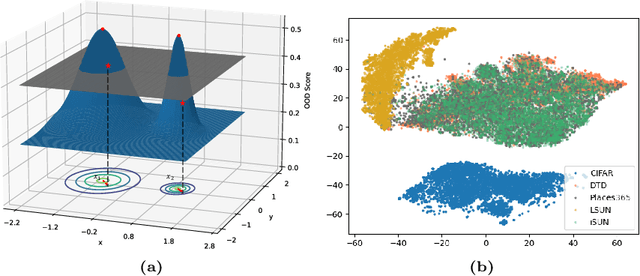
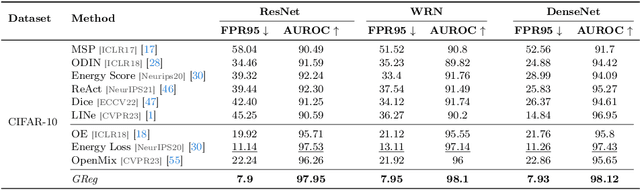
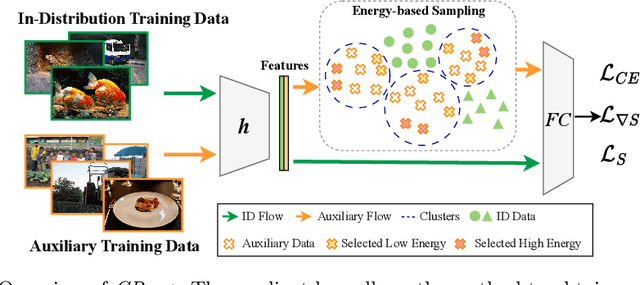
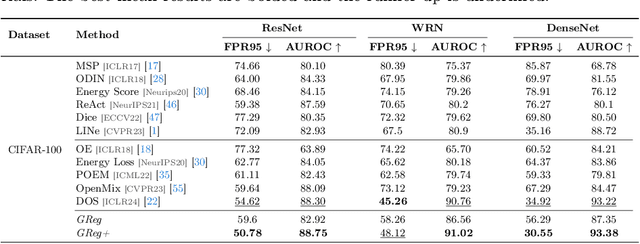
One of the challenges for neural networks in real-life applications is the overconfident errors these models make when the data is not from the original training distribution. Addressing this issue is known as Out-of-Distribution (OOD) detection. Many state-of-the-art OOD methods employ an auxiliary dataset as a surrogate for OOD data during training to achieve improved performance. However, these methods fail to fully exploit the local information embedded in the auxiliary dataset. In this work, we propose the idea of leveraging the information embedded in the gradient of the loss function during training to enable the network to not only learn a desired OOD score for each sample but also to exhibit similar behavior in a local neighborhood around each sample. We also develop a novel energy-based sampling method to allow the network to be exposed to more informative OOD samples during the training phase. This is especially important when the auxiliary dataset is large. We demonstrate the effectiveness of our method through extensive experiments on several OOD benchmarks, improving the existing state-of-the-art FPR95 by 4% on our ImageNet experiment. We further provide a theoretical analysis through the lens of certified robustness and Lipschitz analysis to showcase the theoretical foundation of our work. We will publicly release our code after the review process.

ReachLipBnB: A branch-and-bound method for reachability analysis of neural autonomous systems using Lipschitz bounds

We propose a novel Branch-and-Bound method for reachability analysis of neural networks in both open-loop and closed-loop settings. Our idea is to first compute accurate bounds on the Lipschitz constant of the neural network in certain directions of interest offline using a convex program. We then use these bounds to obtain an instantaneous but conservative polyhedral approximation of the reachable set using Lipschitz continuity arguments. To reduce conservatism, we incorporate our bounding algorithm within a branching strategy to decrease the over-approximation error within an arbitrary accuracy. We then extend our method to reachability analysis of control systems with neural network controllers. Finally, to capture the shape of the reachable sets as accurately as possible, we use sample trajectories to inform the directions of the reachable set over-approximations using Principal Component Analysis (PCA). We evaluate the performance of the proposed method in several open-loop and closed-loop settings.