Deep Learning-Aided Perturbation Model-Based Fiber Nonlinearity Compensation

Fiber nonlinearity effects cap achievable rates and ranges in long-haul optical fiber communication links. Conventional nonlinearity compensation methods, such as perturbation theory-based nonlinearity compensation (PB-NLC), attempt to compensate for the nonlinearity by approximating analytical solutions to the signal propagation over optical fibers. However, their practical usability is limited by model mismatch and the immense computational complexity associated with the analytical computation of perturbation triplets and the nonlinearity distortion field. Recently, machine learning techniques have been used to optimise parameters of PB-based approaches, which traditionally have been determined analytically from physical models. It has been claimed in the literature that the learned PB-NLC approaches have improved performance and/or reduced computational complexity over their non-learned counterparts. In this paper, we first revisit the acclaimed benefits of the learned PB-NLC approaches by carefully carrying out a comprehensive performance-complexity analysis utilizing state-of-the-art complexity reduction methods. Interestingly, our results show that least squares-based PB-NLC with clustering quantization has the best performance-complexity trade-off among the learned PB-NLC approaches. Second, we advance the state-of-the-art of learned PB-NLC by proposing and designing a fully learned structure. We apply a bi-directional recurrent neural network for learning perturbation triplets that are alike those obtained from the analytical computation and are used as input features for the neural network to estimate the nonlinearity distortion field. Finally, we demonstrate through numerical simulations that our proposed fully learned approach achieves an improved performance-complexity trade-off compared to the existing learned and non-learned PB-NLC techniques.

Learning for Perturbation-Based Fiber Nonlinearity Compensation

Several machine learning inspired methods for perturbation-based fiber nonlinearity (PBNLC) compensation have been presented in recent literature. We critically revisit acclaimed benefits of those over non-learned methods. Numerical results suggest that learned linear processing of perturbation triplets of PB-NLC is preferable over feedforward neural-network solutions.

Perturbation Theory-Aided Learned Digital Back-Propagation Scheme for Optical Fiber Nonlinearity Compensation

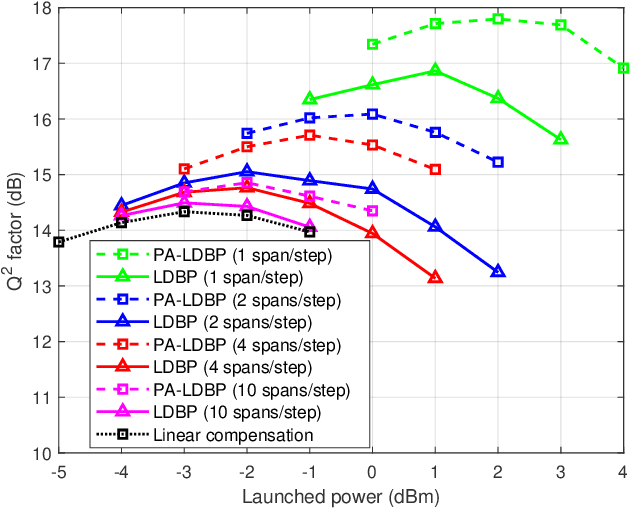
Derived from the regular perturbation treatment of the nonlinear Schrodinger equation, a machine learning-based scheme to mitigate the intra-channel optical fiber nonlinearity is proposed. Referred to as the perturbation theory-aided (PA) learned digital back-propagation (LDBP), the proposed scheme constructs a deep neural network (DNN) in a way similar to the split-step Fourier method: linear and nonlinear operations alternate. Inspired by the perturbation analysis, the intra-channel cross-phase modulation term is conveniently represented by matrix operations in the DNN. The introduction of this term in each nonlinear operation considerably improves the performance, as well as enables the flexibility of PA-LDBP by adjusting the numbers of spans per step. The proposed scheme is evaluated by numerical simulations of a single carrier optical fiber communication system operating at 32 Gbaud with 64-quadrature amplitude modulation and 20*80 km transmission distance. The results show that the proposed scheme achieves approximately 3.5 dB, 1.8 dB, 1.4 dB, and 0.5 dB performance gain in terms of Q2 factor over the linear compensation, when the numbers of spans per step are 1, 2, 4, and 10, respectively. Two methods are proposed to reduce the complexity of PALDBP, i.e., pruning the number of perturbation coefficients and chromatic dispersion compensation in the frequency domain for multi-span per step cases. Investigation of the performance and complexity suggests that PA-LDBP attains improved performance gains with reduced complexity when compared to LDBP in the cases of 4 and 10 spans per step.