Deep Learning-Aided Perturbation Model-Based Fiber Nonlinearity Compensation

Fiber nonlinearity effects cap achievable rates and ranges in long-haul optical fiber communication links. Conventional nonlinearity compensation methods, such as perturbation theory-based nonlinearity compensation (PB-NLC), attempt to compensate for the nonlinearity by approximating analytical solutions to the signal propagation over optical fibers. However, their practical usability is limited by model mismatch and the immense computational complexity associated with the analytical computation of perturbation triplets and the nonlinearity distortion field. Recently, machine learning techniques have been used to optimise parameters of PB-based approaches, which traditionally have been determined analytically from physical models. It has been claimed in the literature that the learned PB-NLC approaches have improved performance and/or reduced computational complexity over their non-learned counterparts. In this paper, we first revisit the acclaimed benefits of the learned PB-NLC approaches by carefully carrying out a comprehensive performance-complexity analysis utilizing state-of-the-art complexity reduction methods. Interestingly, our results show that least squares-based PB-NLC with clustering quantization has the best performance-complexity trade-off among the learned PB-NLC approaches. Second, we advance the state-of-the-art of learned PB-NLC by proposing and designing a fully learned structure. We apply a bi-directional recurrent neural network for learning perturbation triplets that are alike those obtained from the analytical computation and are used as input features for the neural network to estimate the nonlinearity distortion field. Finally, we demonstrate through numerical simulations that our proposed fully learned approach achieves an improved performance-complexity trade-off compared to the existing learned and non-learned PB-NLC techniques.

Learning for Perturbation-Based Fiber Nonlinearity Compensation

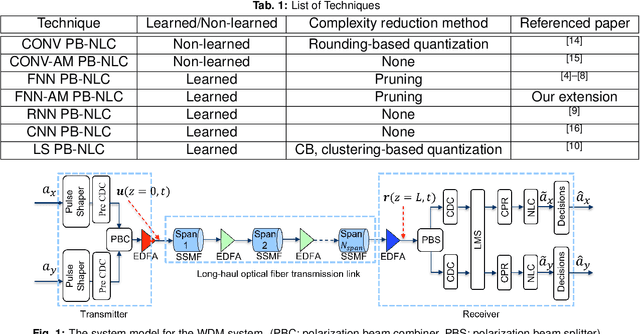
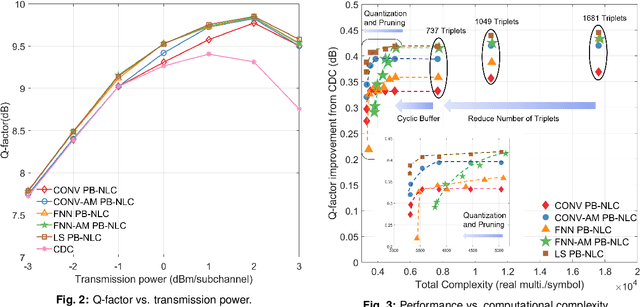
Several machine learning inspired methods for perturbation-based fiber nonlinearity (PBNLC) compensation have been presented in recent literature. We critically revisit acclaimed benefits of those over non-learned methods. Numerical results suggest that learned linear processing of perturbation triplets of PB-NLC is preferable over feedforward neural-network solutions.

Joint PMD Tracking and Nonlinearity Compensation with Deep Neural Networks

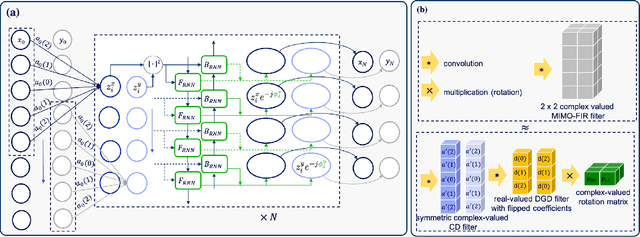
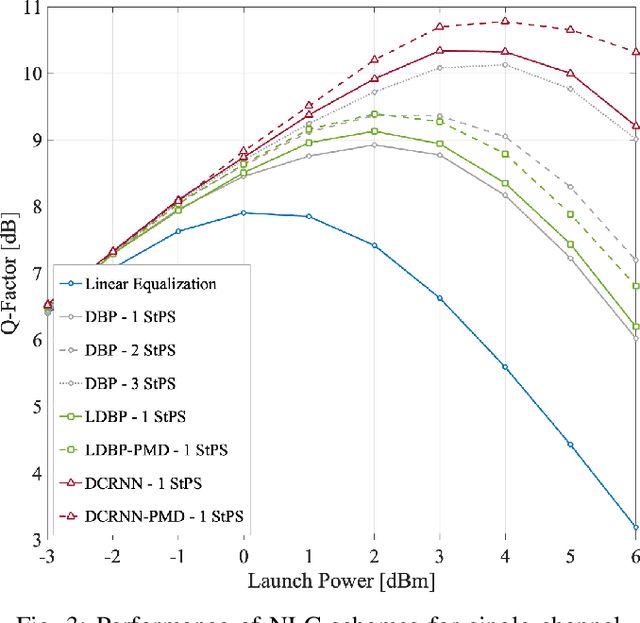
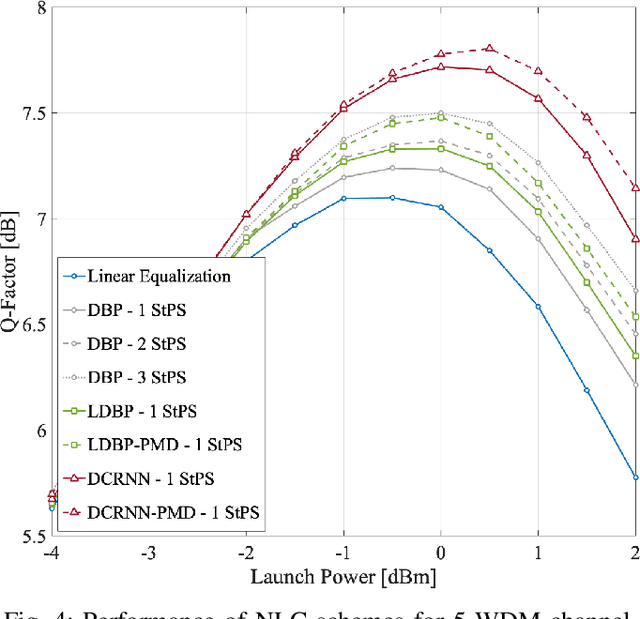
Overcoming fiber nonlinearity is one of the core challenges limiting the capacity of optical fiber communication systems. Machine learning based solutions such as learned digital backpropagation (LDBP) and the recently proposed deep convolutional recurrent neural network (DCRNN) have been shown to be effective for fiber nonlinearity compensation (NLC). Incorporating distributed compensation of polarization mode dispersion (PMD) within the learned models can improve their performance even further but at the same time, it also couples the compensation of nonlinearity and PMD. Consequently, it is important to consider the time variation of PMD for such a joint compensation scheme. In this paper, we investigate the impact of PMD drift on the DCRNN model with distributed compensation of PMD. We propose a transfer learning based selective training scheme to adapt the learned neural network model to changes in PMD. We demonstrate that fine-tuning only a small subset of weights as per the proposed method is sufficient for adapting the model to PMD drift. Using decision directed feedback for online learning, we track continuous PMD drift resulting from a time-varying rotation of the state of polarization (SOP). We show that transferring knowledge from a pre-trained base model using the proposed scheme significantly reduces the re-training efforts for different PMD realizations. Applying the hinge model for SOP rotation, our simulation results show that the learned models maintain their performance gains while tracking the PMD.

Probabilistic Amplitude Shaping and Nonlinearity Tolerance: Analysis and Sequence Selection Method

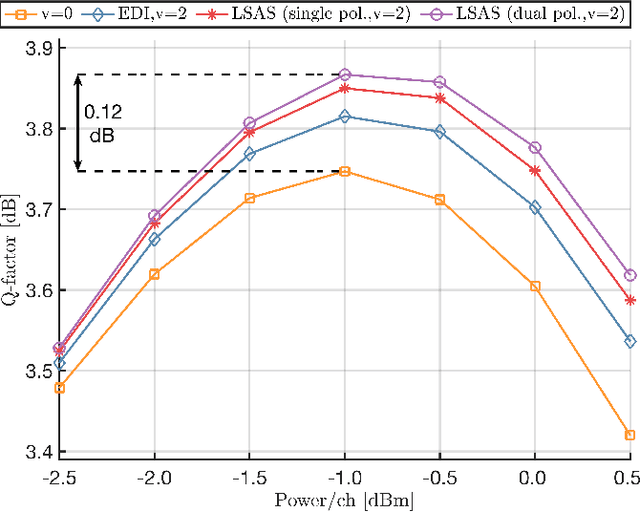
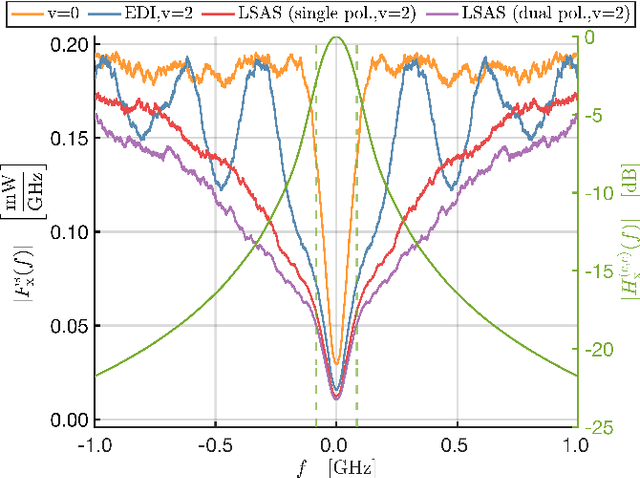
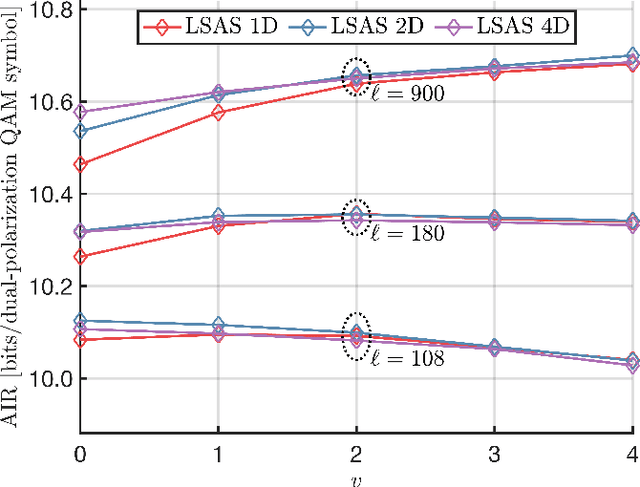
Probabilistic amplitude shaping (PAS) is a practical means to achieve a shaping gain in optical fiber communication. However, PAS and shaping in general also affect the signal-dependent generation of nonlinear interference. This provides an opportunity for nonlinearity mitigation through PAS, which is also referred to as a nonlinear shaping gain. In this paper, we introduce a linear lowpass filter model that relates transmitted symbol-energy sequences and nonlinear distortion experienced in an optical fiber channel. Based on this model, we conduct a nonlinearity analysis of PAS with respect to shaping blocklength and mapping strategy. Our model explains results and relationships found in literature and can be used as a design tool for PAS with improved nonlinearity tolerance. We use the model to introduce a new metric for PAS with sequence selection. We perform simulations of selection-based PAS with various amplitude shapers and mapping strategies to demonstrate the effectiveness of the new metric in different optical fiber system scenarios.

Fiber Nonlinearity Compensation Using Deep Neural Network and Second-Order Perturbation Theory

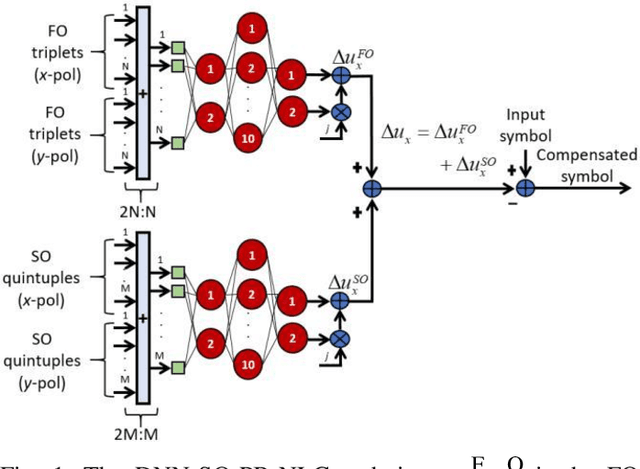
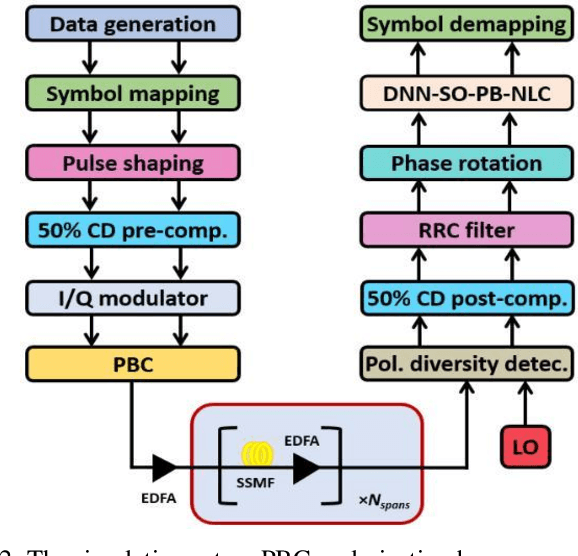
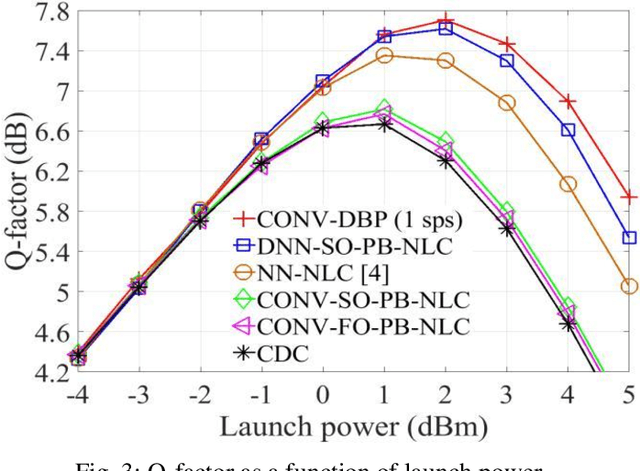
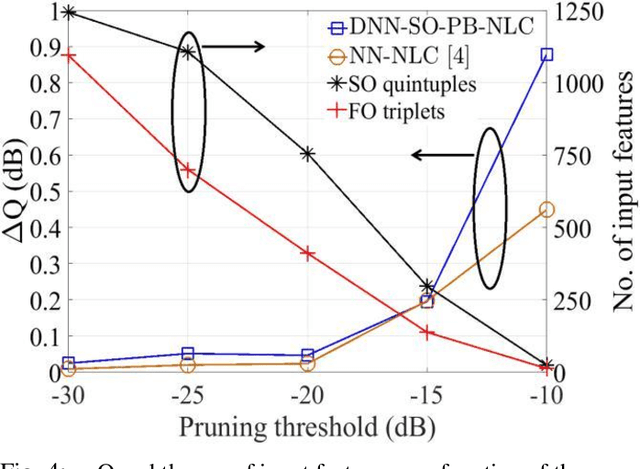
We propose a fiber nonlinearity post-compensation technique using the DNN and the second-order perturbation theory. We achieve 1 dB Q-factor improvement for a 32 Gbaud PDM-64-QAM at 1200 km compared to the linear dispersion compensation.