Deyuan Chang
Perturbation Theory-Aided Learned Digital Back-Propagation Scheme for Optical Fiber Nonlinearity Compensation
Oct 11, 2021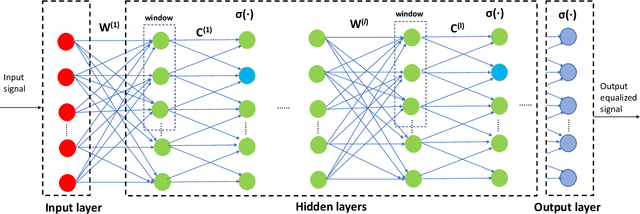

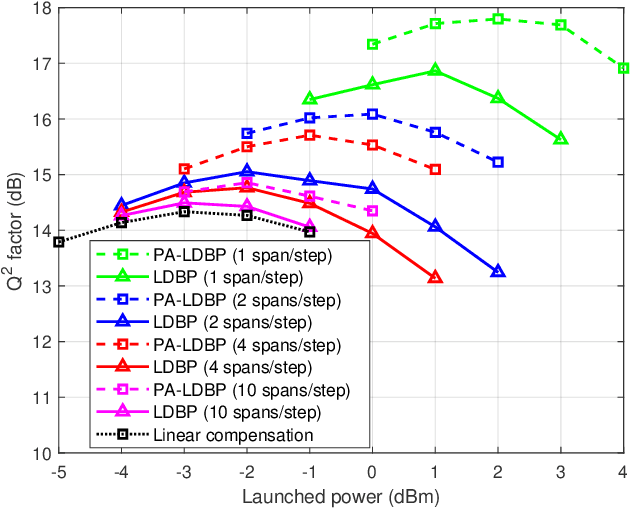
Abstract:Derived from the regular perturbation treatment of the nonlinear Schrodinger equation, a machine learning-based scheme to mitigate the intra-channel optical fiber nonlinearity is proposed. Referred to as the perturbation theory-aided (PA) learned digital back-propagation (LDBP), the proposed scheme constructs a deep neural network (DNN) in a way similar to the split-step Fourier method: linear and nonlinear operations alternate. Inspired by the perturbation analysis, the intra-channel cross-phase modulation term is conveniently represented by matrix operations in the DNN. The introduction of this term in each nonlinear operation considerably improves the performance, as well as enables the flexibility of PA-LDBP by adjusting the numbers of spans per step. The proposed scheme is evaluated by numerical simulations of a single carrier optical fiber communication system operating at 32 Gbaud with 64-quadrature amplitude modulation and 20*80 km transmission distance. The results show that the proposed scheme achieves approximately 3.5 dB, 1.8 dB, 1.4 dB, and 0.5 dB performance gain in terms of Q2 factor over the linear compensation, when the numbers of spans per step are 1, 2, 4, and 10, respectively. Two methods are proposed to reduce the complexity of PALDBP, i.e., pruning the number of perturbation coefficients and chromatic dispersion compensation in the frequency domain for multi-span per step cases. Investigation of the performance and complexity suggests that PA-LDBP attains improved performance gains with reduced complexity when compared to LDBP in the cases of 4 and 10 spans per step.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge